Примеры выполнения заданий.
Пример
1.
Найти область решении системы неравенств
,
,
,
.
Решение:
Заменяя
знаки неравенств на знаки точных
равенств, получим уравнения четырех
прямых:
,
,
,
,
изображенных на рис. 1. Приведем данные
неравенства к виду
,
,
,
.
Штриховка показывает те из полуплоскостей,
которые служат областями решения
соответствующих неравенств. Областью
решений системы неравенств является
выпуклый четырехугольник.
Ответ: Выпуклый четырехугольник АВСД.
Пример
2.
Максимизировать линейную форму
при
ограничениях:
,
,
.
Решение:
Заменив
знаки неравенств на знаки точных
равенств, построим область решений по
уравнениям прямых
,
,
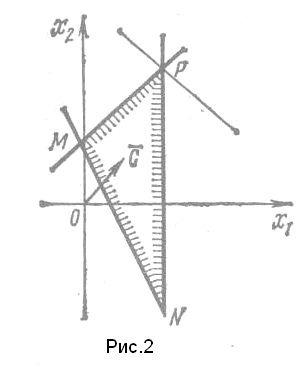
(рис. 2).
Областью
решений неравенств является треугольник
MNP.
Построим вектор С (2; 2). Тогда опорная
прямая при выходе из треугольника
решений пройдет через точку Р(3;
15/2), а потому в точке
Р
линейная функция
принимает наибольшее значение, т. е.
максимизируется, и
.
Ответ: .
Пример 3.
Минимизировать линейную функцию
при ограничениях:
,
,
,
.
Решение:
Заменив
знаки неравенств на знаки точных
равенств, построим область решений,
ограниченную прямыми
,
,
,
.
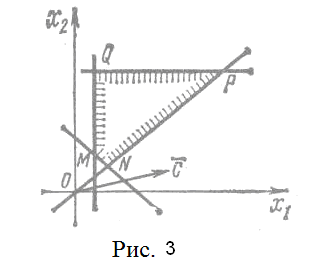
Область решений — многоугольник
MNPQ
(рис. 3). Строим вектор С (12; 4). Опорная
прямая проходит через точку М (1/2; 3/2) —
это первая точка пересечения многоугольника
решений с прямой L
при перемещении этой прямой в положительном
направлении вектора С. В точке
М
линейная функция
принимает наименьшее значение
.
Ответ:
Пример
4.
Максимизировать линейную форму
при ограничениях:
,
,
.
Решение:
Данная система уравнений - ограничений совместна, так как ранги матрицы системы
и расширенной матрицы
совпадают
и равны 3. Следовательно, система уравнений
совместна и три переменные (базисные)
можно линейно выразить через две
свободные переменные. Выразим, например
,
и
через
и
,
т.е. приведем систему к единичному
базису:
(*)
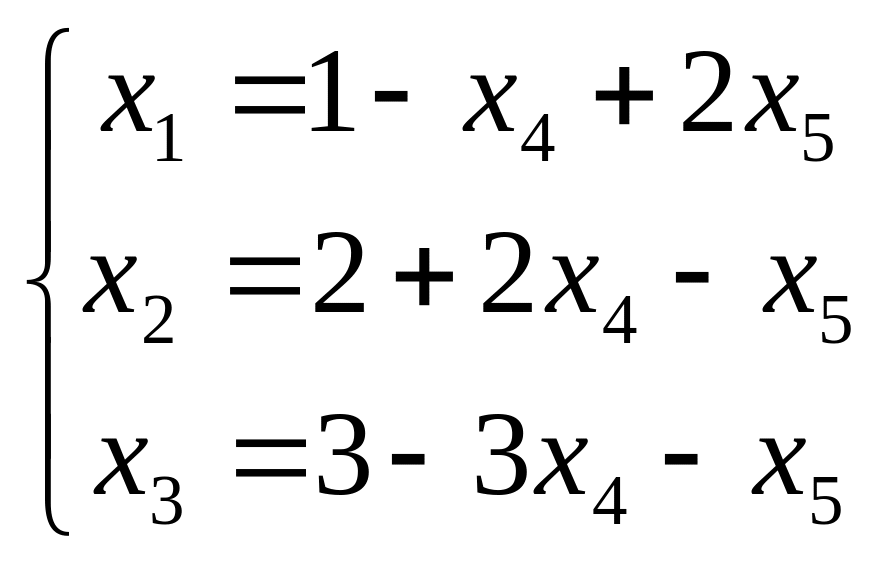Линейную
форму
выразим через свободные переменные
и
(в данном примере
L
уже выражена через
и
).
Теперь при
и
найдем
значения базисных переменных:
,
,
.
Таким образом, первое допустимое решение
системы уравнений есть
,
,
,
,
или (1, 2, 3, 0, 0). При найденном допустимом
решении линейная форма L
имеет значение 0, т. е.
.
Теперь
попытаемся увеличить значение
;
увеличение
х4
уменьшит
,
так как перед
стоит отрицательный коэффициент, а
увеличение
дает увеличение и
.
Увеличим поэтому
так, чтобы
,
,
не стали отрицательными, оставив
.
Из второго уравнения системы
(*)
следует, что
можно увеличить до 2. Таким образом,
получаем следующие значения переменных:
,
,
,
,
или (5, 0, 1, 0, 2).
Значение
линейной формы
при этом допустимом решении равно
,
т е при втором шаге оно увеличилось.
Далее,
примем за свободные переменные
и
,
т. е. именно те переменные, которые в
новом решении имеют нулевые значения.
С этой целью из второго уравнения системы
(*)
выразим
через
и
и
получим
.
Тогда
(**)
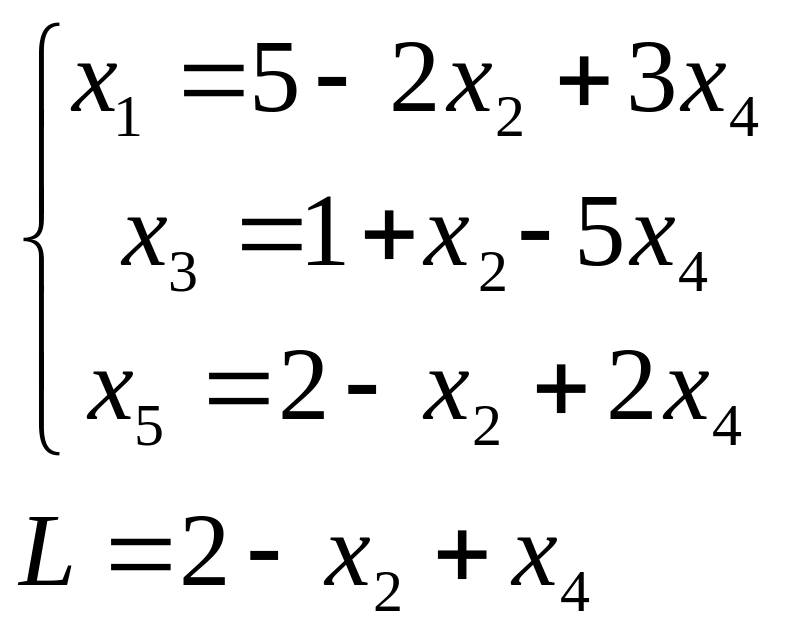Для
увеличения значения
будем увеличивать
.
Из системы (**) видно, что при условии
неотрицательности
значение
можно довести до
.
При этом условии новое допустимое
решение есть
,
,
,
,
или (
,
0, 0,
,
).
Значение линейной формы при этом
.
Выразим теперь , , через свободные переменные и :
(***)
Так
как в последней линейной форме обе
свободные переменные входят с
отрицательными коэффициентами, то
наибольшее значение L
достигается при
,
.
Это означает, что решение (
,
0, 0,
,
)
является оптимальным и
.
Ответ: решение ( , 0, 0, , ), .
Пример
5.
Задана система ограничений:
,
и линейная форма
.
Найти оптимальное решение, минимизирующее
линейную форму.
Решение:
Данная система уравнений совместна, так как ранги матрицы системы и расширенной матрицы одинаковы и равны 2. Следовательно, систему уравнений можно, например, переписать так:
Здесь
за базисные переменные приняты
и
,
а за свободные
и
.
При
и
первое базисное решение есть
,
,
,
или (2, 1, 0, 0), а
.
Уменьшение линейной формы L
вызывается увеличением
,
так как перед
в форме L
стоит отрицательный коэффициент, причем
увеличение
возможно только до 1, а значение
остается. Если примем
,
то
,
,
,
или (0, 1, 1, 0) – второе базисное решение,
при котором
.
Выразим и через новые свободные переменные и :
Теперь
уменьшение значения формы
L
зависит от увеличения
до
(при этом
неотрицательно),
а значение
остается. В этом
случае
имеем новое допустимое решение
,
,
,
или (0, 0,
,
),
при котором
.
Выразим и через свободные переменные и :
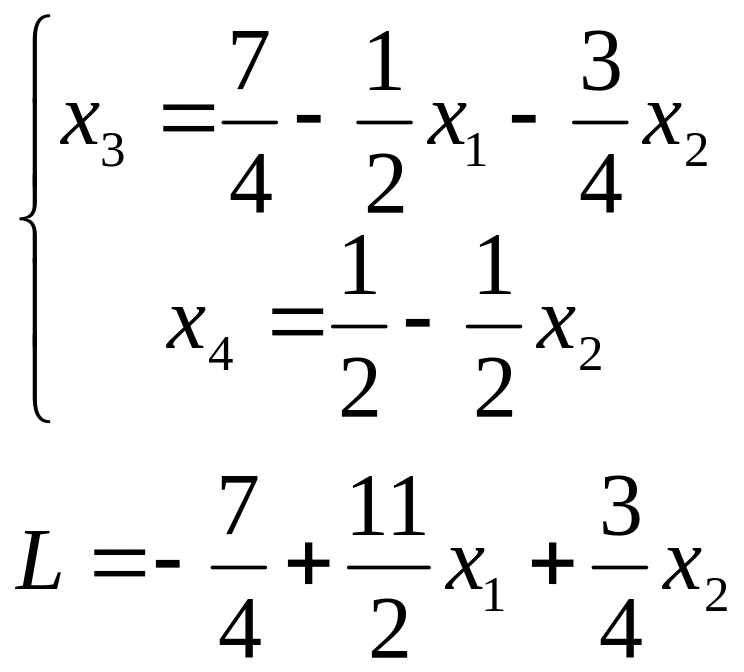
Так
как дальнейшее уменьшение значения
формы L
невозможно из-за положительности
коэффициентов при
и
,
то допустимое решение задачи (0, 0,
,
)
является оптимальным. Наименьшее
значение L
равно
.
Ответ:
(0, 0,
,
),
.
Задания для практической работы.
Вариант 1.
1. Найти область
решений системы неравенств:
,
,
.
2. Найти наибольшее
значение функции
при ограничениях:
,
,
.
3. Найти оптимальные
неотрицательные решения, минимизирующие
линейную форму:
.
Вариант 2.
1. Найти область
решений системы неравенств:
,
,
.
2. Минимизировать
функцию
при ограничениях:
,
,
.
3. Найти оптимальные
неотрицательные решения, минимизирующие
линейную форму:
.