Задания для практической работы. Вариант 1.
1.
Решите уравнение:
.
2.
Решите уравнение:
.
3.
Найти частное решение дифференциального
уравнения
,
если
.
4.
Найти частное решение дифференциального
уравнения
,
если
.
Вариант 2.
1.
Решите уравнение:
2.
Решите уравнение:
3.
Найти частные решения дифференциальных
уравнений:
,
если
4.
Найти частные решения дифференциальных
уравнений:
,
если
Практическая работа № 6.
Тема: Решение систем линейных алгебраических неравенств.
Цели работы: научиться находить область решений систем линейных неравенств, научиться находить наибольшее (наименьшее) значение линейной формы геометрическим и симплекс-методом.
Краткое изложение темы.
1. Область решений системы линейных неравенств.
Если задана система неравенств
,
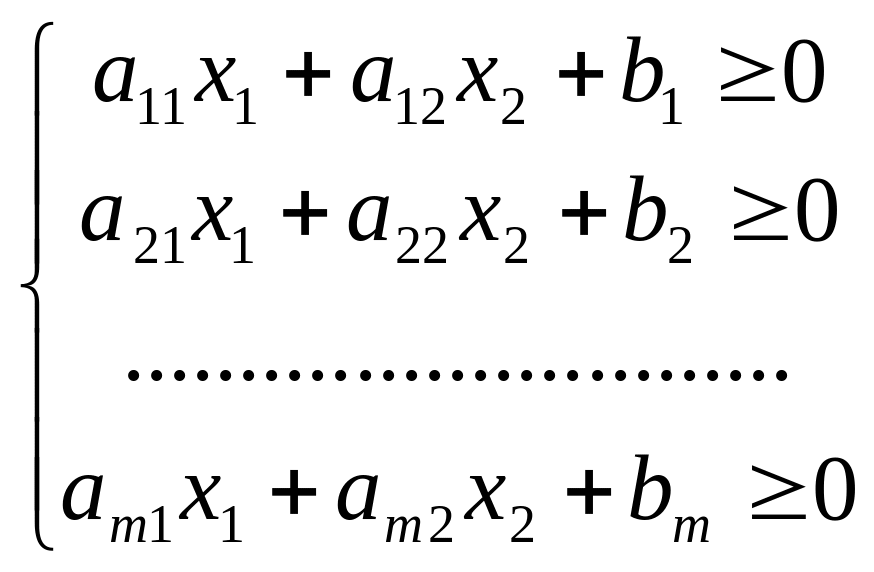где
- конечное число, получим пересечение
конечного числа полуплоскостей,
образующее многоугольную область
.
Область
называется областью
решений
системы неравенств. Эта область не
всегда бывает ограничена, она может
быть и неограниченной и даже пустой.
Область решений обладает важным свойством – она является выпуклой, т.е. вместе с любыми своими двумя точками содержит и весь соединяющий их отрезок.
2. Основная задача линейного программирования.
Задача линейного программирования заключается в изучении способов отыскания наибольшего или наименьшего значений линейной функции при наличии линейных ограничений.
Функция, наибольшее или наименьшее значение которой отыскивается, называется целевой функцией, а совокупность значений переменных, при которых достигается наибольшее или наименьшее значение, определяет так называемый оптимальный план. Всякая же другая совокупность значений, удовлетворяющая ограничениям, определяет допустимый план (решение).
Пусть ограничения заданы совместной системой линейных неравенств с переменными:
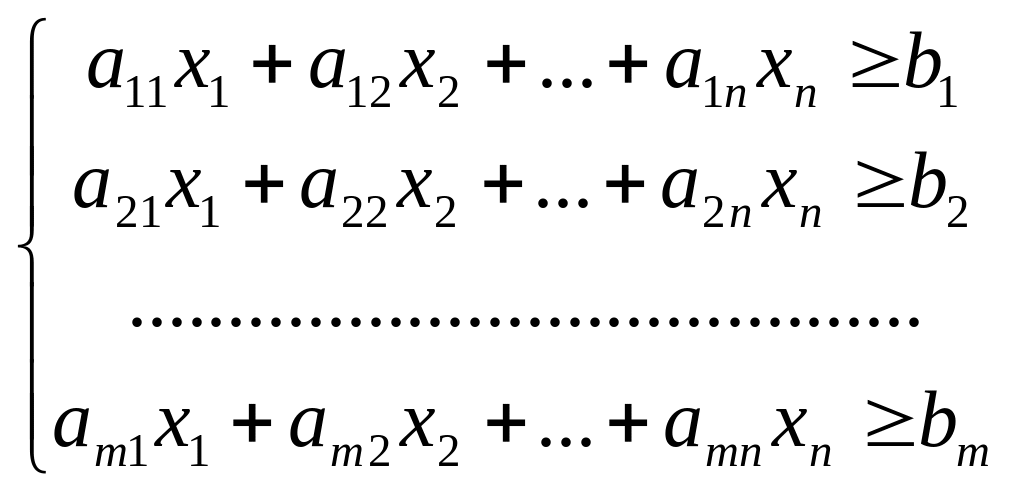
Среди неотрицательных решений этой системы требуется найти такое решение при котором линейная функция (целевая функция),
принимает наибольшее (наименьшее) значение или, как говорят, максимизировать (минимизировать) линейную форму L.
Геометрический метод решения задачи:
Есть
совместная система линейных неравенств
с двумя и тремя переменными. Пусть, кроме
того, задана линейная функция
.
Найдем
среди множества точек
из области решений совместной системы
неравенств такие, которые придают
заданной линейной функции наименьшее
(наибольшее) значение. Для каждой точки
плоскости функция L
принимает фиксированное значение
.
Множество всех таких точек есть прямая
перпендикулярная вектору
,
выходящему из начала координат. Если
эту прямую передвигать параллельно
самой себе в положительном направлении
вектора С,
то линейная функция
будет возрастать, а в противоположном
направлении - убывать. Пусть при движении
прямой
в положительном направлении вектора С
она впервые встретится с многоугольником
решений в его вершине, тогда в этом
положении
прямая
становится опорной,
и на этой прямой функция
принимает наименьшее значение. При
дальнейшем движении в том же направлении
(положительном) прямая
пройдет через другую вершину многоугольника
решений,
выходя из
области решений, и станет также опорной
прямой
;
на ней функция
принимает наибольшее значение среди
всех значений, принимаемых на многоугольнике
решений.
Таким образом, минимизация и максимизация линейной функции на многоугольнике решений достигаются в точках пересечения этого многоугольника с опорными прямыми, перпендикулярными вектору . Опорная прямая может иметь с многоугольником решений либо одну общую точку (вершину многоугольника), либо бесконечное множество точек (это множество есть сторона многоугольника).
Симплекс-метод.
Система ограничений в вычислительных методах обычно задается системой линейных уравнений
(1)
и среди неотрицательных решений, системы уравнений надо найти такие, которые максимизировали бы линейную функцию
.
1.
Выразим
,
,
…,
через остальные переменные:
(2)
где
,
,
…,
.
Переменные
,
,
…,
называются
базисными,
а весь набор
—
базисом,
остальные переменные называются
свободными,
система
ограничений (2) называется
системой,
приведённой к единичному базису.
Подставляя
в линейную форму L
вместо базисных переменных их выражения
через свободные из системы (2), получим
.
2.
Теперь, полагая все свободные переменные
равными нулю, найдем значения базисных
переменных:
,
,
…,
.
Таким образом, решение
(
,
,
…,
,
0, …, 0) системы является допустимым —
оно называется
базисным.
Для
полученного базисного решения значение
линейной формы
.
Решение задачи с помощью, симплекс-метода
распадается на ряд шагов, заключающихся
в том, что от данного базиса Б мы переходим
к другому базису Б' с таким расчетом,
чтобы значение
уменьшалось или, по крайней мере, не
увеличивалось, т. е.
.
Идею метода проследим на конкретных примерах, которые приведены ниже.