
- •Практическая работа № 1. Тема: Вычисление определителей. Действия над матрицами.
- •Краткое изложение темы.
- •Примеры выполнения заданий.
- •Задания для практической работы. Вариант 1
- •Вариант 2
- •Практическая работа № 2.
- •Краткое изложение темы.
- •Примеры выполнения заданий.
- •Практическая работа № 3.
- •1. Дифференцирование явных функций.
- •Примеры выполнения заданий.
- •3. Дифференцирование неявных функций.
- •Задания для практической работы. Вариант № 1.
- •Вариант № 2.
- •Практическая работа № 4.
- •Краткое изложение темы.
- •Примеры выполнения заданий.
- •Задания для практической работы. Вариант 1.
- •Вариант 2.
- •Практическая работа № 5.
- •Краткое изложение темы.
- •Примеры выполнения заданий.
- •Задания для практической работы. Вариант 1.
- •Вариант 2.
- •Практическая работа № 6.
- •Краткое изложение темы.
- •1. Область решений системы линейных неравенств.
- •2. Основная задача линейного программирования.
- •Примеры выполнения заданий.
- •Практическая работа № 7.
- •Примеры выполнения заданий.
- •Задания для практической работы. Вариант 1.
- •Вариант 2.
- •Практическая работа № 8. Тема: Действия над комплексными числами.
- •Краткое изложение темы.
- •Примеры выполнения заданий.
- •Практическая работа № 9.
- •Примеры выполнения заданий.
- •Задания для практической работы. Вариант 1.
- •Вариант 2.
- •Практическая работа № 10.
- •Краткое изложение темы.
- •Примеры выполнения заданий.
- •Задания для практической работы. Вариант 1.
- •Вариант 2.
- •Приложения.
Примеры выполнения заданий.
Пример 1. Построить дискретный вариационный ряд и начертить полигон для следующего распределения 45 пар мужской обуви, проданных магазином за день:
39 |
41 |
40 |
42 |
41 |
40 |
42 |
44 |
40 |
43 |
42 |
41 |
38 |
43 |
42 |
41 |
40 |
41 |
38 |
44 |
43 |
41 |
43 |
39 |
42 |
41 |
42 |
39 |
41 |
37 |
40 |
39 |
41 |
40 |
42 |
40 |
41 |
42 |
40 |
43 |
38 |
39 |
41 |
41 |
42 |
|
|
|
|
|
Решение:
Для построения вариационного ряда различные значения признака располагаем в порядке их возрастания и под каждым из этих значений записываем его частоту.
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
1 |
3 |
5 |
8 |
12 |
9 |
5 |
2 |
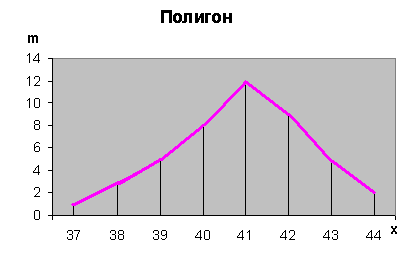
Полигон этого распределения изображен на рисунке.
Пример 2. Наблюдения за толщиной (в мм) 50 слюдяных прокладок дали следующие результаты:
0,021 |
0,030 |
0,039 |
0,031 |
0,042 |
0,034 |
0,036 |
0,030 |
0,028 |
0,031 |
0,030 |
0,033 |
0,027 |
0,031 |
0,045 |
0,028 |
0,030 |
0,033 |
0,027 |
0,031 |
0,036 |
0,028 |
0,024 |
0,031 |
0,040 |
0,031 |
0,033 |
0,031 |
0,034 |
0,027 |
0,030 |
0,048 |
0,030 |
0,046 |
0,043 |
0,030 |
0,033 |
0,028 |
0,031 |
0,051 |
0,034 |
0,031 |
0,036 |
0,034 |
0,037 |
0,030 |
0,039 |
0,031 |
0,042 |
0,037 |
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 0,020—0,024, второй—0,024—0,028 и т.д.) и начертить гистограмму.
Решение:
Для построения вариационного ряда составим таблицу, в первом столбце которой расположим в порядке возрастания интервалы, а во втором займемся подсчетом соответствующих частот:
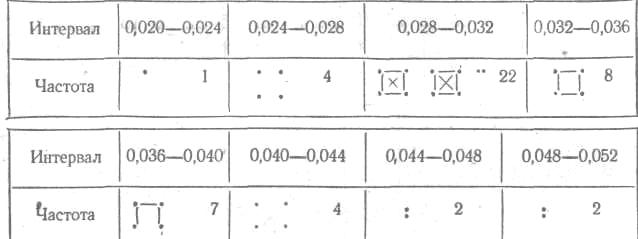
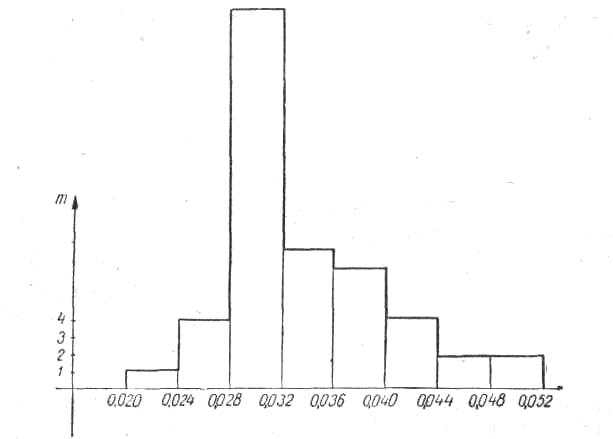
Гистограмма этого распределения изображена на рисунке.
Пример 3. Найти моду и медиану распределения:
Интервал |
120-140 |
140-160 |
160-180 |
180-200 |
200-220 |
220-240 |
240-260 |
260-280 |
Частота |
1 |
6 |
19 |
58 |
53 |
24 |
16 |
3 |
Решение:
Так
как наибольшая частота
![]() отвечает интервалу 180-200, то
отвечает интервалу 180-200, то
![]() =180,
=19,
=53
и
=180,
=19,
=53
и
![]() .
.
Для нахождения медианы строим кумулятивный ряд:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Интервал |
120-140 |
140-160 |
160-180 |
180-200 |
200-220 |
220-240 |
240-260 |
260-280 |
Накопленная частота |
1 |
7 |
26 |
84 |
137 |
161 |
177 |
180 |
Номер медианного интервала s определяется из неравенств
,
или, то же самое
![]() ,
,
![]() .
.
В
нашем случае
![]() ,
,
![]() и
и
![]() .
Поэтому медианным интервалом является
200-220, а
.
Поэтому медианным интервалом является
200-220, а

Ответ:
![]() ,
,
![]() .
.
