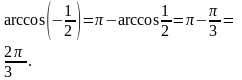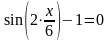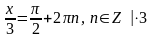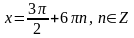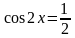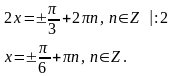- •Глава VIII тригонометрия
- •§ 1. Формулы приведения
- •2. Алгоритм перехода от углов (1) к углу :
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •§ 2. Вычисление значений тригонометрических функций
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Решение тригонометрических уравнений
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Тригонометрическими функциями
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
Задание для самостоятельного решения
143) Решите уравнение:
а) sin x = 0; в) tg x = -1; д) sin x = 2; ж) cos x = - 3;
б)
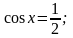 г)
г)
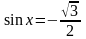 ;
е)
;
е)
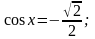 з)
з)
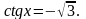
Если вы решаете тригонометрическое уравнение, которое не является простым уравнением, то в конечном результате вы должны свести его путём тождественных преобразований к одному или нескольким простейшим уравнениям.
ПРИМЕРЫ. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
144. Решите уравнение
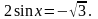
Решение:
|: 2
|
145. Решите уравнение
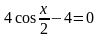 .
.
Решение:
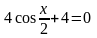
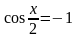
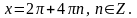
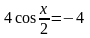 | : 4
| : 4
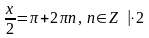 Ответ:
Ответ:
146. Решите уравнение
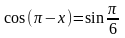 .
.
Решение: Преобразуем
данное уравнение, используя
формулу приведения и найдя значение
Имеем,
|
cos(π – x) = - cos x;
|
147) Решите уравнение
а) 1 – tg 2x
= 0; в) 5cos 3x
+ 4 = 0; д)
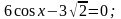
б)
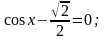 г)
г)
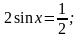 е)
е)
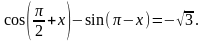
148) Решите уравнение
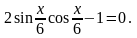
Р ешение:
ешение:
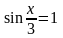
синус двойного угла
|
|
149) Решите уравнение cos2x – sin2x =0,5.
Р ешение:
cos2x
– sin2x
=0,5
ешение:
cos2x
– sin2x
=0,5
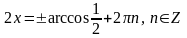
косинус двойного угла
|
|
150)
Решите уравнение
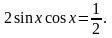
151) Найдите все решения уравнения
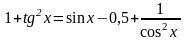 .
.
Решение: Применим формулу
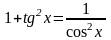 .
.
Имеем уравнение,
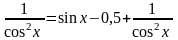 .
Приведём подобные слагаемые, имеем
.
Приведём подобные слагаемые, имеем
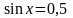
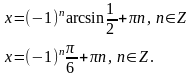
152)
Решите уравнение
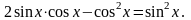
154)
Найдите все решения уравнения
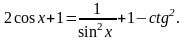
155)
Найдите все решения уравнения
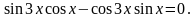
156)
Решите уравнение
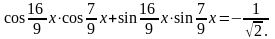

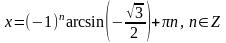
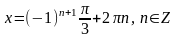
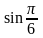 .
.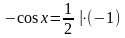
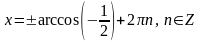
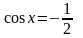
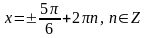
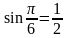 ;
;