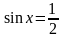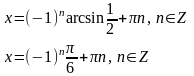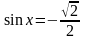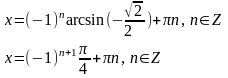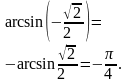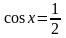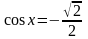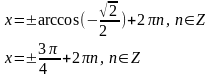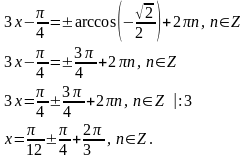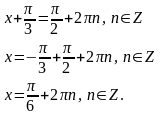- •Глава VIII тригонометрия
- •§ 1. Формулы приведения
- •2. Алгоритм перехода от углов (1) к углу :
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •§ 2. Вычисление значений тригонометрических функций
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Решение тригонометрических уравнений
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Тригонометрическими функциями
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
Задание для самостоятельного решения
1.
Найдите значение выражения
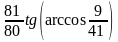 .
.
Решение простейших тригонометрических уравнений
Простейшими тригонометрическими уравнениями называются уравнения вида sin x = a
cos x = a
tg x = a
ctg x = a
I. Уравнение sin x = a

1 Если
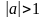 ,
то уравнение решений не имеет.
,
то уравнение решений не имеет.
а [-1;1]
Например: а) sin x = 1,1;
б) sin x = - 100; решений нет
в) sin x = .
2 При
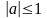 имеет место формула
имеет место формула
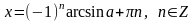 .
.
а [-1;1]
 3 Частные случаи
а = 0;
1.
3 Частные случаи
а = 0;
1.

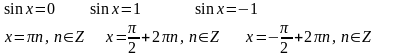
Пример. Решите уравнение
а)
Решение:
|
б)
Решение:
|
|
в) sin x = 0,9
Решение: :
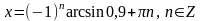
I. Уравнение cos x = a
1 Если , то уравнение решений не имеет.
а [-1;1]
Например: а) cos x = 5,3;
б)
cos
x
=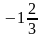 ;
решений нет
;
решений нет
в) cos
x
=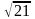 .
.
2 При
имеет место формула
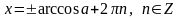 .
.
а [-1;1]
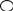 3 Частные случаи
а = 0;
1.
3 Частные случаи
а = 0;
1.
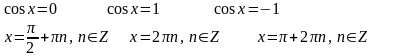
Пример. Решите уравнение
а)
Решение:
в) cos
x =
|
б)
Решение:
|
|
Решение:

III. Уравнение tg x = a
Уравнение tg x = a имеет решение при любом значении а, так как областью значения функции tg x являются все числа.
Для
любого а имеет место формула
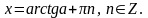
Пример. Решите уравнение
а) tg x = 1 б) tg x = 100 г) tg x = - 3,4
Решение: Решение: Решение:
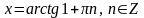
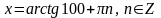
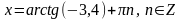
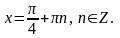
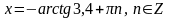
IV. Уравнение ctg x = a
Уравнение ctg x = a имеет решение при любом значении а, так как областью значения функции ctg x являются все числа.
Для
любого а имеет место формула
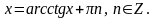
Пример. Решите уравнение
а) ctg x = -1 б) tg x = 5,7 г) сtg x = 0
Решение: Решение: Решение:
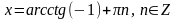
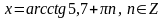
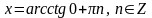

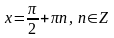
К простейшим уравнениям так же относятся уравнения вида
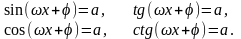
Их следует решать по тем же формулам, что и уравнения
sin x = a, tg x = a,
cos x = a, ctg x = a,
заменив х на ωх + φ.
Пример 1. Пример 2.
Решите
уравнение
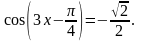 Решите уравнение
Решите уравнение
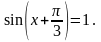
Решение:
|
Решение:
|