
- •Глава VIII тригонометрия
- •§ 1. Формулы приведения
- •2. Алгоритм перехода от углов (1) к углу :
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •§ 2. Вычисление значений тригонометрических функций
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Решение тригонометрических уравнений
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Тригонометрическими функциями
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
Задания для самостоятельного решения
141)
Вычислите а) arctg 0; б)
arctg(-1); в)
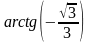 г)
г)
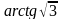 .
.
Арккотангенс.
На
промежутке
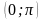 функция у = сtg
x
убывает и принимает на нём все свои
значения, то есть значения от - ∞ до +
∞. Поэтому на промежутке
для функции у = сtg
x
существует обратная функция.
Она обозначается у
= arcсtg
x
(читается «арккотангенс х»).
функция у = сtg
x
убывает и принимает на нём все свои
значения, то есть значения от - ∞ до +
∞. Поэтому на промежутке
для функции у = сtg
x
существует обратная функция.
Она обозначается у
= arcсtg
x
(читается «арккотангенс х»).
Свойства функции у = аrcсtg x
Область определения функции – множество всех действии тельных чисел.
Область значения функции – промежуток .
Функция не является ни чётной, ни нечётной.
Функция убывающая.
Так как записи у = arсctg x и х = сtg y эквивалентны, то
арккотангенсом числа х R называется такое число у , котангенс которого равен х.

Помни.
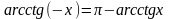
Задания для самостоятельного решения
142)
Вычислите а) arcсtg
1; б) arcсtg
(-1); в)
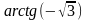 .
.
Некоторые задания связанные с обратными
Тригонометрическими функциями
Пример 1. Постройте график функции у = cos (arсcos x).
Решение.
cos (arсcos
x) = х где
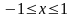
Имеем, у = х.
 у
у
1
0 1 х
Пример 2. Найти: а) аrcsin (sin 1,2); б) arcsin (sin 8).
Решение.
а) По определению аrcsin
(sin х) = х, где
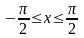 .
.
В
нашем случае
 ,
поэтому аrcsin (sin
1,2) = 1,2.
,
поэтому аrcsin (sin
1,2) = 1,2.
б) По определению аrcsin (sin х) = х, где .
В нашем случае число 8 . Заменим sin 8 синусом другого угла х, удовлетворяющему неравенству .
 sin
8 = sin(3π – 8)
sin
8 = sin(3π – 8)
y 1,42
8
x
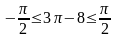
Поэтому arcsin (sin 8) = arcsin (sin(3π – 8)) = 3π – 8.
Пример
3. Найдите значение выражения
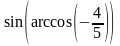
Решение. Пусть Эта
запись означает, что
Так, как значением косинуса яв – 0 ляется отрицательное число, то у – угол II четверти.
|
ПОЯСНЕНИЕ Обозначив
получили = sin y. Поэтому для решения задачи нам осталось найти sin y.
|
Так
как у – угол II четверти,
а во второй четверти знач ение синуса
положительно, то
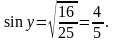
Ответ:
=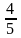 .
.
Пример
4. Найдите значение выражения
 .
.
Решение.
Пусть
 .
.
Эта
запись означает, что
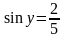 и
и
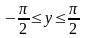 .
Определим углом какой четверти является
у. Так как
.
Определим углом какой четверти является
у. Так как
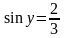 ,
т.е значение синуса положительно, то
,
т.е значение синуса положительно, то
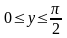 т.е у – угол I четверти.
т.е у – угол I четверти.
tg
y = ? 1)
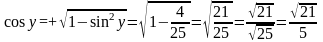
2)
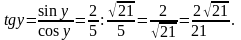
Ответ:
=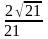 .
.

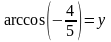 .
.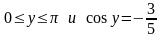 .
.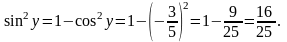
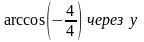 ,
мы
,
мы