Задания для самостоятельного решения

137) Вычислите а) arcsin 0; б) arcsin 1; в) .

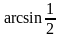Эта формула позволяет находить значения

арксинусов отрицательных чисел через зна -

чения арксинусов положительных чисел.

Например: а) ; б) .

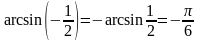Задания для самостоятельного решения

138) Вычислите а) 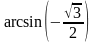; б) arcsin (-1).

Арккосинус.

у

1

у = cos x

π

0 х

-1

На отрезке [0;π] функция у = cos x убывает и областью её значений является отрезок [- 1;1]. Значит, для функции у = cos x, рассматриваемой на отрезке [0;π], существует обратная функция. Эту функцию обозначают у = аrccos x (читается «арккосинус х»).

Свойства функции у = аrccos x

1. Область определения – отрезок [- 1;1].

2. Область значения функции – отрезок [0;π].

3. Функция не является ни чётной, ни нечётной.

4. Функция убывающая.

Так как записи у = аrccos x и х = cos у эквивалентны, то

арккосинусом числа х [- 1;1] называется такое число у [0;π], косинус которого равен х.

.

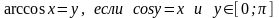Пример. Вычислите .

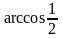Решение: По определению 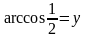, если 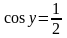и у [0;π].

Таким образом .

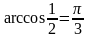Задания для самостоятельного решения

139) Вычислите а) аrccos 0; б) arсcos 1; в) .

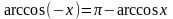Эта формула позволяет находить значения

арккосинусов отрицательных чисел через

значения арккосинусов положительных чисел.

Пример. а) ;

б) .

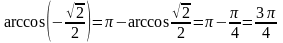Задания для самостоятельного решения

140) Вычислите а) ; б) arсcos (- 1).

Арктангенс.

На промежутке 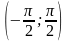функция у = tg x возрастает и принимает на нём все свои значения, то есть значения от - ∞ до + ∞. Поэтому на промежутке для функции у = tg x существует обратная функция. Она обозначается у = arctg x (читается «арктангенс х»).

Свойства функции у = аrctg x

1. Область определения функции – множество всех действительных чисел.

2. Область значения функции – промежуток .

3. Функция нечётная:.

4. Функция возрастающая.

Так как записи у = arctg x и х = tg y эквивалентны, то

арктангенсом числа х R называется такое число у , тангенс которого равен х.

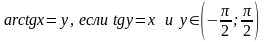
Помни. arctg(-x) = - arctg x