
- •Глава VIII тригонометрия
- •§ 1. Формулы приведения
- •2. Алгоритм перехода от углов (1) к углу :
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •§ 2. Вычисление значений тригонометрических функций
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Решение тригонометрических уравнений
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Тригонометрическими функциями
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
Задания для самостоятельного решения
131) Упростите выражение cos 7α cos 6α + cos α - sin 3α sin 5α.
132) Упростите выражение sin 4α cos 6α + sin(π – α) - sin 6α cos 4α.
ФОРМУЛЫ ДВОЙНОГО УГЛА
sin 2x = 2sin x cos x
cos 2x = cos2x – sin2x = 2cos2x – 1= 1 – 2sin2x
Эти
формулы позволяют выразить тригонометрические
функции синуса и косинуса какого нибудь
угла, углом в два раза меньше. Например,
с помощью этих формул можно от угла
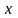 перейти к углу
перейти к углу
 ,
от угла 4х перейти к углу 2х и так далее.
,
от угла 4х перейти к углу 2х и так далее.
Примеры применения формул двойного угла
1. Упрощение выражений.
Пример. Упростите выражение
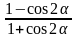 .
.
Решение:

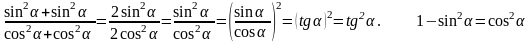
2. Вычисление значений тригонометрических выражений.
Пример 1. Вычислите
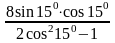 .
.
Решение: Упростим дробь. Для этого в числители дроби применим формулу синуса двойного угла, а в знаменатели формулу косинуса двойного угла.
= =
=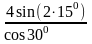 =
=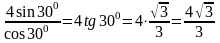 .
.
Если в знаменатели мы не увидели косинус двойного угла, то вычисления можно было произвести иначе.
1
= sin2150
+ cos2150.
Имеем,
= =
=
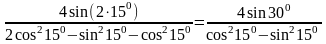 =
.
=
.

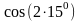
Пример 2. Найдите значение выражения
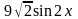 ,
если
,
если
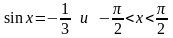 .
.
Решение: Применим формулу двойного угла. Имеем,
x – угол IV четверти, поэтому cos s > 0. Имеем,
Тогда
Ответ: - 8. |
Пояснение
Так как , то х – угол IV четверти (в I четверти sinx > 0)
|
Пример
3.Найдите значение функции
 в точке
в точке
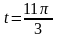 .
.
Решение: Не забыли совет: если угол выражен в радианах и не является табличным углом, то лучше перевести радианы в градусы.
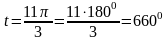
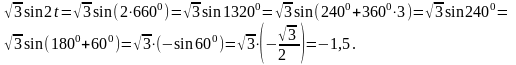
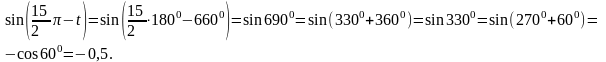 Тогда
=
- 1,5 – 0,5 = - 2.
Тогда
=
- 1,5 – 0,5 = - 2.
Ответ: - 2.
Замечания:
1) При нахождении значения функции мы радианы перевели в градусы, но если:
а) вы хорошо считаете устно;
б) умеете свободно владеть формулами приведения, в которых углы записаны в радианах,
то радианы в градусы можно было не переводить.
2)
При нахождении значения выражения
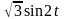 можно было применить формулу синуса
двойного угла.
можно было применить формулу синуса
двойного угла.
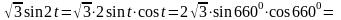 и т.д.
и т.д.
Задания для самостоятельного решения
133)
Упростите выражение
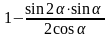 .
1) 2cos3α;
2) sin2α;
3) cos α;
4) cos2α.
.
1) 2cos3α;
2) sin2α;
3) cos α;
4) cos2α.
134
В) Упростите выражение
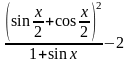 .
.
135
В) Вычислите
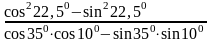 .
1) – 1; 2)
;
3)
;
4) 1.
.
1) – 1; 2)
;
3)
;
4) 1.
136
В) Найдите значение выражения 25sin2x,
если
 .
.
Решение тригонометрических уравнений
**ОБРАТНАЯ ФУНКЦИЯ
Рассмотрим две функции y = f(x) и y = g(x) графики которых изображены на рисунке 1.
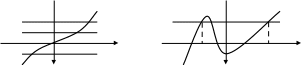
у у
y = f(x) y = g(x)
х х1 х2 х
Рис. 1
Функция
y
= f(x)
каждое своё значение принимает один
единственный раз т.е для любых двух
значений аргумента х1
и х2
f(x1)
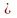 f(x2).
Геометрически это означает: любая
горизонтальная прямая, которая пересекает
график функции пересекает его только
в одной точке.
f(x2).
Геометрически это означает: любая
горизонтальная прямая, которая пересекает
график функции пересекает его только
в одной точке.
Функция y = f(x) называется обратимой, если каждое своё значение она принимает один единственный раз.
Функция y = g(x) является необратимой. Например х1 х2, но g(x1) = g(x2). Геометрически это означает: горизонтальная прямая, которая пересекает график функции пересекает его более чем в одной точке (на рисунке таких точек пересечения три).
Если функция у = f(x) обратима, то выразив х из формулы у = f(x) и поменяв затем х и у местами получим обратную функцию.
Пример.
Функция
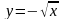 обратима. D(y)
= [0; +∞),
обратима. D(y)
= [0; +∞),
y y = x2
x
Рис. 2 |
E(y) = (- ∞;0]. Задав любое у из промежутка [0; +∞) можно найти соответствующее х по формуле х = у2. Функция х
= у2 при у
есть функция, обратная к функции Так как выбор букв для обозначения независимого и зависимого переменного несущественен поменяв местами х и у получим функцию у = х2 при х 0, которая является обратной функции . На рисунке 2 изображены графики взаимно обратных функций и у = х2. |
ПОМНИ.
Если функция
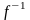 является обратной функции
является обратной функции
 ,
то:
,
то:
Областью определения обратной функции является множество значений функции , а множество значений есть область определения функции ;
Графики и симметричны относительно прямой у = х.
Функцией, обратной к обратной функции , является исходная функция. Таким образом, функции и всегда взаимно обратны.
Теорема (об обратной функции).Если функция у = f(х) определена и возрастает (или убывает) на промежутке X и областью её значений является промежуток Y, то у неё существует обратная функция, причём обратная функция определена и возрастает (или убывает) на Y.
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
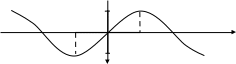
Арксинус.
у
1
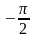 х
х
- 1 у = sin x
На
отрезке
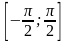 функция у =sin
x
возрастает и областью её значений
является отрезок [-1;1].Значит, для функции
у =sin
x,
рассматриваемой на отрезке
существует обратная функция. Эту функцию
обозначают у = arcsin
x
(читается «арксинус
х»).
функция у =sin
x
возрастает и областью её значений
является отрезок [-1;1].Значит, для функции
у =sin
x,
рассматриваемой на отрезке
существует обратная функция. Эту функцию
обозначают у = arcsin
x
(читается «арксинус
х»).
Свойства функции у = arcsin x
1. Область определения – отрезок [- 1;1];
2. Область значений – отрезок ;
3. Функция нечётная: arcsin (- x) = - arcsin x;
4. Функция возрастающая.
Так как записи у = arcsin x и x = sin y эквивалентны, то
арксинусом числа х [- 1;1] называется такое число у , синус которого равен х.
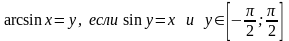
Пример.
Вычислить: а)
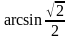 ;
б)
;
б)
 .
.
Решение:
а) По определению
=
у, если
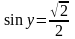 и у
и у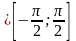 .
.
Таким
образом
=
.
б)
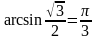 .
.

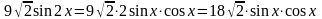 .
. ,
найдём cos x.
,
найдём cos x.
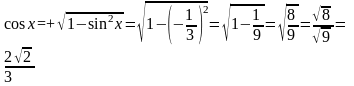
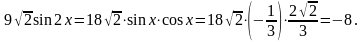
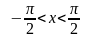 ,
поэтому х является углом либо I
четверти, либо углом IV
четверти.
,
поэтому х является углом либо I
четверти, либо углом IV
четверти.





 0
0