
- •Глава VIII тригонометрия
- •§ 1. Формулы приведения
- •2. Алгоритм перехода от углов (1) к углу :
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •§ 2. Вычисление значений тригонометрических функций
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Решение тригонометрических уравнений
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Тригонометрическими функциями
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
Задание для самостоятельного решения
125) Вычислите: а) sin 7650; б) cos (- 36300); в) tg (- 5850); г) ctg9300.
СОВЕТ. Если α выражен не в градусах, а в радианах и не является табличным значением, то есть α ≠ 0, , , , , то лучше радианы перевести в градусы.
Помни, π = 1800.
Пример.
Вычислите значение выражения
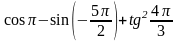 .
.
Р ешение:
ешение:
=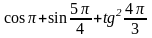 =
=
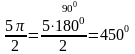 .
.
=cos1800
+ sin 4500 + tg2
2400 = -1 +1 +(
)2
= 3.
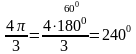 .
.
Ответ: 3. cos1800 = - cos 00 = -1.
sin 4500 = sin(900 +3600) = sin 900 = 1.
tg 2400 = tg (1800 + 600) = tg 600 =
Задание для самостоятельного решения
126)
Найдите значение выражения
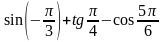 .
.
1) 1 - ; 2) 2; 3) 1 + ; 4) 1.
СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ
ФУНКЦИЯ ОДНОГО И ТОГО ЖЕ АРГУМЕНТА
|
ПРИМЕНЕНИЕ 1. Упрощение выражений. Пример
1. Упростите выражение
Решение:
Пример 2. Упростите выражение - 9sin2x + 4 – 9cos2x. Решение: - 9sin2x + 4 – 9cos2x = сгруппируем = (- 9sin2x – 9cos2x) + 4 = -
9(sin2x
+ cos2x)
+ 4 = 1 |
Пример
3. Упростите выражение
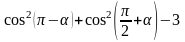 .
.
Решение: Применим формулы приведения:
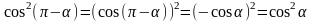 .
.
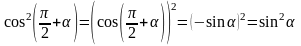 .
.
Имеем, = cos2α + sin2α – 3 = (cos2α + sin2α) – 3 = 1 – 3 = - 2.
2. Нахождение значения выражения.
Пример
1. Найдите значение выражения
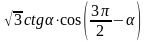 ,
если
,
если
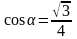 .
.
Решение: Применяя формулу приведения и формулу 3 имеем,
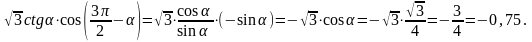
Ответ: - 0,75.
Пример
2. Найдите значение выражения сtg
α, если
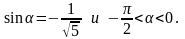
Решение:
Первый способ.
Тогда
|
Второй
способ. Применим формулу
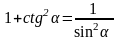 .
.
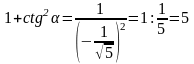
Имеем, 1 + сtg2α = 5. сtg2α = 4. Найдём ctg α.
т.е α – угол IV
четверти. Значит ctg α
< 0. Имеем,
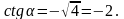
Ответ: - 2.
Задания для самостоятельного решения
127) Упростите выражение 8sin2x – 10 + 8cos2x.
1) 18; 2) – 18; 3) – 2; 4) 6sin2x cos2x.
128) Упростите выражение sin4x + sin2x cos2x. 1) sin2x; 2) sin x; 3) 2sin6x cos2x; 4) 1.
129)
Упростите выражение
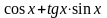 .
.
1) 1; 2) 2 cos x;
3) cos x +
sin x; 4)
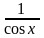 .
.
130)
Найдите значение выражения
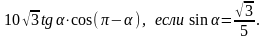
ФОРМУЛЫ СЛОЖЕНИЯ
sin(x + y) = sin x cos y + cos x sin y cos(x + y) = cos x cos y – sin x sin y
sin(x – y) = sin x cos y – cos x sin y cos(x – y) = cos x cos y + sin x sin y
Примеры применения формул сложения при упрощении выражений.
Пример1. Упростите выражение cos 3α cos 5α – cos 2α + sin 3α sin 5α .
Решение: cos 3α cos 5α – cos 2α + sin 3α sin 5α = (cos 3α cos 5α + sin 3α sin 5α) – cos 2α =
 cos(3α
- 5α) – cos 2α
= cos(-2α) –
cos 2α =
cos(3α
- 5α) – cos 2α
= cos(-2α) –
cos 2α =
cos(3α - 5α) cos2α – cos 2α = 0.
Пример
2. Упростите выражение
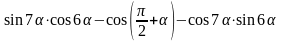 .
.
Решение: Применим для упрощения выражения формулу синуса разности двух углов и формулу приведения.
=
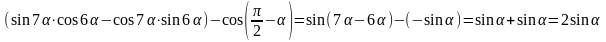
- sinα


 .
.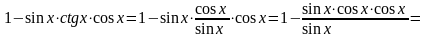
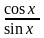 1-
cos2x
= sin2x.
1-
cos2x
= sin2x.

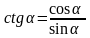 .
Значение синуса α
известно, найдём значение косинуса
α.
.
Значение синуса α
известно, найдём значение косинуса
α.
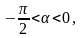 т.е α
– угол IV четверти поэтому
cosα > 0. Имеем,
т.е α
– угол IV четверти поэтому
cosα > 0. Имеем,
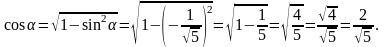
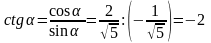 Ответ: -2.
Ответ: -2.