
- •Глава VIII тригонометрия
- •§ 1. Формулы приведения
- •2. Алгоритм перехода от углов (1) к углу :
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •§ 2. Вычисление значений тригонометрических функций
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Решение тригонометрических уравнений
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Тригонометрическими функциями
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
Задания для самостоятельного решения
122) Вычислите:
а) sin 600; в) tg
450; д)
 ;
ж) sin 1800; и)
tg π; л)
;
ж) sin 1800; и)
tg π; л)
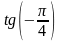 ;
;
б) cos 300; г)
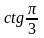 ;
е) cos 0; з)
;
е) cos 0; з)
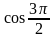 ;
к) sin (- 450); м)
;
к) sin (- 450); м)
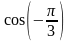 .
.
123)
Вычислите: а)
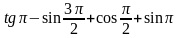 ;
б) 5sin 900 + 2cos
00 – 2sin2700 +
10cos1800;
;
б) 5sin 900 + 2cos
00 – 2sin2700 +
10cos1800;
в)
 .
.
2случай. является углом II или III или IV четвертей и, причём < 3600
II 1800 III IV 3600
2700
|
Для нахождения значений тригонометрических функций этих углов, применяя формулы приведения, переходим к острому углу, то есть к углу I четверти и находим значение соответствующей тригонометрической функции.
|
Пример: Вычислите sin 1200
Решение: 1200 – угол II четверти, поэтому 1200 можно представить как
900 900 + 300 1200 = 900 + 300
или то есть или и применяя формулу
1200 1800 - 600 1200 = 1800 - 600
1800 приведения перейдём к углу 300 или 600.
Имеем,
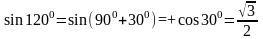
или
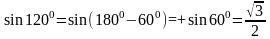
При вычислении значения тригонометрической функций отрицательного угла, переходим к положительному углу, применяя чётность или нечётность соответствующей функции.
Пример. Вычислите tg(-3150).
3150
3600
2700 |
Р
угол IV четверти поэтому 3150 = 2700 + 450 или 3150 = 3600 - 450 |
Задания для самостоятельного решения
124) Вычислите:
а) sin3300; б) sin(-2250); в) cos1200; г) cos(-3150); д) ctg2400; e) ctg(-1350).
3cлучай. > 3600.
Для нахождения значений тригонометрических функций углов больше 3600 применяется свойство периодичности функций.
Функции
sin
α
и cos
α
имеют период 2πn,
где n
= 0;
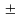 1;
2;…
.
1;
2;…
.
2π – наименьший период функций sin α и cos α.
Справедливы равенства
1) sin(α + 2πn) = sin(α + 3600n) = sin α
где n = 0; 1; 2;…
2) cos (α + 2πn) = cos (α + 3600n) = cos α
Пример 1. Вычислите cos11100.
Решение: Выясним, сколько целых оборотов содержится в 11100.
1110 360 1080 3 30 |
Поэтому угол 11100
можно представить в виде 11100 =
300 +
Используя равенство 2) имеем
|
Пример 2. Вычислите sin(-40050).
Перейдём к Выясним, сколько
Р ешение:
sin(-40050) =
положительному -sin40050
= целых
оборотов -
ешение:
sin(-40050) =
положительному -sin40050
= целых
оборотов -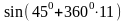 =
=
углу содержится в 40050
sin (- α) = -sin α и используем ра -
венство 1)
= -
sin 450=
 .
.
4005 360
360
405
360
45 Имеем, 40050 =
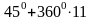
Функции tg α и ctg α имеют период πn, где n = 0; 1; 2;… .
π – наименьший период функций tg α и ctg α.
Справедливы равенства
1) tg(α + πn) = tg(α + 1800n) = tg α
где n = 0; 1; 2;…
2) ctg (α + πn) = ctg (α + 1800n) = ctg α
П ример
1. Вычислите tg 5400.
540 180
ример
1. Вычислите tg 5400.
540 180
Решение:
tg 5400 = tg
(00 +
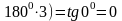 .
540 3
.
540 3
0 Имеем, 5400 = 00
+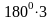
Пример 2. Вычислите ctg (- 18450).
Решение:
ctg (- 18450) = - ctg
18450 = -
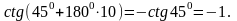
Пояснение: ctg (-α) = - ctg α 1845 180
180 10
45
0
45
Имеем,

 900
900

 ешение:
tg(-3150)
= - tg 3150
= -tg(3600 –
450)
= - (- tg 450)
= tg 450
= 1.
ешение:
tg(-3150)
= - tg 3150
= -tg(3600 –
450)
= - (- tg 450)
= tg 450
= 1.
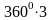 .
.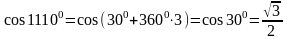 .
.