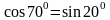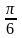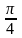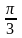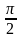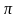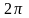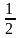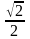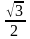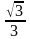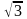- •Глава VIII тригонометрия
- •§ 1. Формулы приведения
- •2. Алгоритм перехода от углов (1) к углу :
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •§ 2. Вычисление значений тригонометрических функций
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Решение тригонометрических уравнений
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Задания для самостоятельного решения
- •Тригонометрическими функциями
- •Задание для самостоятельного решения
- •Задание для самостоятельного решения
Задания для самостоятельного решения
120) Упростите выражение:
а) sin(900 +
);
д) cos(1800 -
);
и)
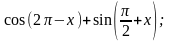
б) tg(900 +
);
е) sin(2700 +
);
к) cos x +
cos(900 –x)
+
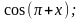
в)
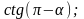 ж)
ж)
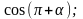 л)
л)
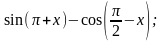
г) sin(3600 -
);
з)
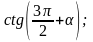 м)
м)
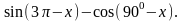
Если
нам даны не углы
,
,
,
,
,
,
,
(1), а углы им
противоположные
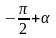 ,
,
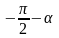 ,
,
 ,
,
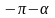 ,
,
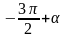 ,
,
 ,
,
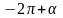 ,
,
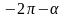 (2), то применяя формулы, выражающие
зависимость между синусами, косинусами,
тангенсами и котангенсами противоположных
углов
(2), то применяя формулы, выражающие
зависимость между синусами, косинусами,
тангенсами и котангенсами противоположных
углов
sin(- ) = - sin (функция синус нечётная)
сos(- ) = cos (функция косинус чётная)
tg(- ) = - tg (функция тангенс нечётная)
ctg(- ) = - ctg (функция котангенс нечётная)
переходим от углов (2) к углам (1).
Пример 2. Упростите выражение:
а)
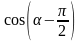 ;
б)
;
б)
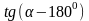 .
.
Решение:
а)
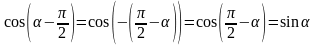
или короче
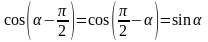 .
.
б)
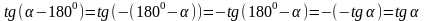
или короче
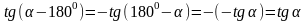 .
.
Задания для самостоятельного решения
121) Упростите выражение:
а)
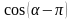 ;
в)
;
в)
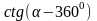 ;
.
;
.
б)
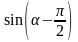 ;
г)
;
г)
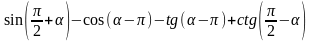 .
.
§ 2. Вычисление значений тригонометрических функций
Значения тригонометрических функций
некоторых углов
|
00 |
300 |
450 |
600 |
900 |
1800 |
2700 |
3600 |
Помни.
1.
Если
Пример:
а)
б)
2. 900
Значения тригоно – 1800 метрических функций 00 данных углов 3600 противоположны |
0 |
|
|
|
|
|
|
|
||
sin |
0 |
|
|
|
1 |
0 |
-1 |
0 |
|
cos |
1 |
|
|
|
0 |
-1 |
0 |
1 |
|
tg |
0 |
|
1 |
|
– |
0 |
– |
0 |
|
ctg |
– |
|
1 |
|
0 |
– |
0 |
– |
2700
Задача. Найдите значение sin , cos , tg или ctg .
Решение:
При нахождении значений sin , cos , tg или ctg возможны три случая.
1случай. принимает значение одного из следующих углов
00 |
300 |
450 |
600 |
900 |
1800 |
2700 |
3600 |
0 |
|
|
|
|
|
|
|
то есть является табличным значением. Поэтому для нахожде -
ния значений тригонометрических функций этих углов применяем таблицу.
Пример.
Вычислите а) sin 300;
б)
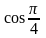 ;
в)
;
в)
 ;
г)
;
г)
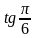 .
.
Решение: Используя таблицу значений тригонометрических функций некоторых углов, имеем: а) sin 300 = ; б) = ; в) = 0; г) = .
Е сли
мы находим значения тригонометрических
функций не табличных углов, а им
противоположных (отрицательных), то
используя чётность или нечётность
тригонометрических функций переходим
от отрицательного аргумента к
положительному аргументу.
сли
мы находим значения тригонометрических
функций не табличных углов, а им
противоположных (отрицательных), то
используя чётность или нечётность
тригонометрических функций переходим
от отрицательного аргумента к
положительному аргументу.
Пример: а) sin
(- 300) =
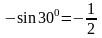 ;
sin(-
)
= - sin
;
sin(-
)
= - sin
б)
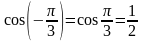 ;
сos(-
)
= cos
;
сos(-
)
= cos
в) tg(- π) = - tg π = - 0 = 0; tg(- ) = - tg
г)
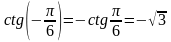 .
ctg(-
)
= - ctg
.
ctg(-
)
= - ctg

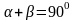 ,
то
,
то

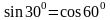 ;
;