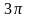Глава VIII тригонометрия

§ 1. Формулы приведения

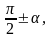
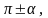
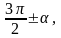
Формулы приведения позволяют выразить тригонометрические функции углов 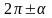(1) через тригонометрические функции угла .

Если свести все формулы приведения в таблицу, то получим:

х
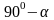
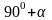
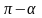
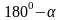
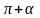
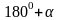
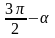
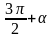
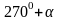
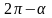
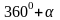
sin x	cos	cos	sin	-sin	-cos	-cos	-sin	sin
cos x	sin	-sin	-cos	-cos	-sin	sin	cos	cos
tg x	ctg	-ctg	-tg	tg	ctg	-ctg	-tg	tg
ctg x	tg	-tg	-ctg	ctg	tg	-tg	-ctg	ctg

Что мы видим? Мы видим 32 формулы, которые мы должны знать. Но запоминать наизусть их не надо! Чтобы вспомнить формулу приведения нужно только хорошо знать: 1) Знаки тригонометрических функций по четвертям;

2) Алгоритм перехода от углов (1) к углу .

1. Знаки тригонометрических функций по четвертям;

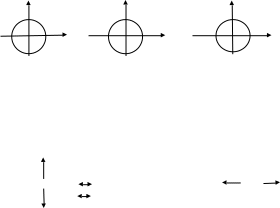
у у у

II I II I II I

+ + – + – +

– – x – + x + – x

III IV III IV III IV

Знаки синуса Знаки косинуса Знаки тангенса и котангенса

2. Алгоритм перехода от углов (1) к углу :

1) Определяем углом какой четверти является данный угол.

! считаем острым углом.

2) Определяем знак функции в этой четверти.

3) Задаём вопрос: «Меняем название функции?»

ОТВЕТ ДА sin cos 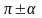НЕТ

tg ctg

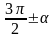ДА или НЕТ как кивок головой.

Пример 1. Замените тригонометрической функцией угла .

а) 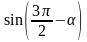; б) ctg (360⁰ + );

Решение: Решение:

1) - угол III четверти. 1) 360⁰ + - угол I четверти.

+

360⁰

-

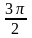
2) Синус в III четверти имеет знак минус. 2) Котангенс в I четверти имеет знак плюс

3) Меняем название функции? 3) Меняем название функции?

Да, синус на косинус. Нет.

Таким образом = - cos . Таким образом ctg (360⁰ + ) = +ctg .

в) ;

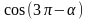Решение:

1) - угол II четверти. 2) Косинус во II четверти имеет знак минус.

3) Меняем название функции?

Нет.

Таким образом = - cos .

-