Билет 7.

_1.Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S,встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В,лежащей на линии, соединяющей S с центром отверстия (рис. 259).

         

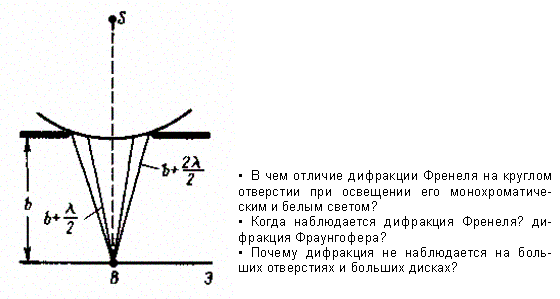
                                                Рис. 259

 

Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)),

где знак плюс соответствует нечетным m и минус - четным m.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А =А₁, т.е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием (см. § 177). Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если тнечетное - то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то A_m ≪ A₁ и результирующая амплитуда A = A₁/2, т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.

2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем иа экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260).

 

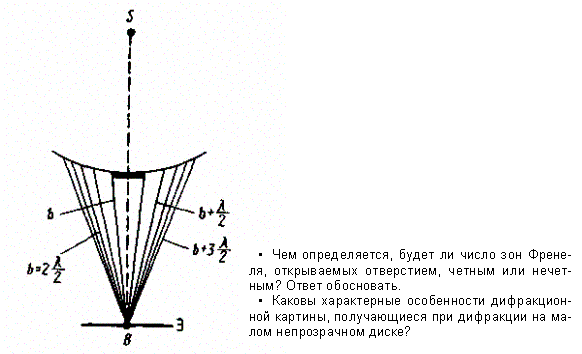
                                      Рис. 260

В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает т первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

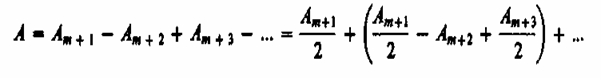
 или

 

 так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается угол j_т (см. рис. 258) между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.

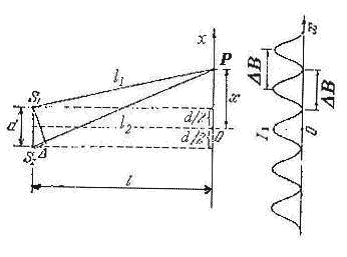
2. ИНТЕРФЕРЕНЦИЯ СВЕТА - пространственное перераспределение энергии светового излучения при наложении двух или неск. световых волн, частный случай общего явления интерференции волн. Рассмотрим более подробно основные свойства интерференционной картины, создаваемой двумя источниками электромагнитных волн одинаковой интенсивности и наблюдаемой на плоском экране, расположенным на расстоянии   от плоскости расположения от источников. В качестве таких источников могут мыслиться, например две бесконечно-узкие, параллельные друг - другу щели или два отверстия бесконечно малого диаметра, расстояние между которыми  , прорезанные в плоском непрозрачном экране (рис. 4.3a). Пусть источники электромагнитных волн располагаются в однородной среде с показателем преломления  .

Рис. 4.3a.

Область, в которой волны источников перекрываются, называется полем интерференции. В поле интерференции имеются места, где волны источников будут складываться в фазе. В этих местах будут отмечаться максимумы интенсивности электромагнитного поля. Там же, где волны будут складываться в противофазе - минимальная интенсивность . Если в поле интерференции поместить непрозрачный экран, то будет наблюдается чередование светлых и тёмных полос (рис. 4.3a), представляющие собой интерференционную картину. Параметрами интерференционной картины являются положение её максимумов   и минимумов  , а также связанная с ними ширина полос интерференционной картины   (рис. 4.3a).

В соответствии с (4.4a) для расчёта этих величин надо найти разность фаз   излучаемых источниками волн в точке наблюдения, расположенной на экране. Как показано в главе 3, для расчёта   надо определить оптическую разность хода  волн от первого и второго источников (рис. 4.3a) до точки наблюдения, поскольку

,

где   - показатель преломления среды, в которой распространяются электромагнитные волны;   - расстояния, проходимые волнами соответственно от первого и второго источников (рис. 4.3a) до точки наблюдения;   - длина волны.

Из рис. 4.3a имеем очевидные соотношения, определяющие расстояния  :

(4.6a)

(4.6b)

Отсюда следует, что

Принимая во внимание, что   при условии  , получаем:

.

Использование этого соотношения приводит к следующему выражению для оптической разности хода волн  :

.

(4.7)

Максимум интерференционной картины будет наблюдаться при условии синфазного сложения колебаний волн источников, которое имеет место при   . Исходя из связи между разностью фаз колебаний и оптической разностью хода  , можно заключить, что синфазное сложение колебаний имеет место при условии кратности оптической разности хода целому числу длин волны   в среде :

,

(4.8)

где   - произвольное целое число, равное  .

Найдём координату  , определяющую положение   - ого максимума интерференционной картины:

,

(4.9a)

где   - длина волны в вакууме, связанная с длиной волны   в среде распространения с помощью формулы  .

Порядком интерференционного максимума называют его номер ' ', отсчитываемый от центрального ( ), которому соответствует центр интерференционной картины , где складываются волны от источников, проходящие одинаковый путь ( ) .

Аналогичным образом можно найти положения минимумов интерференционной картины двух источников, определяемые координатами  , если положить оптическую разность хода кратной нечётному числу полуволн:

.

(4.9b)

где   - произвольное целое число, равное  .

Отсюда следует, что в рассматриваемой интерференционной картине положения соседних интерференционных максимумов и минимумов находятся на одинаковом расстоянии друг от друга и не зависят от того, насколько эти максимумы удалены от центра интерференционной картины. Это свойство максимумов и минимумов позволяет определить ширину интерференционной полосы.

Ширина интерференционной полосы определяется, как расстояние между соседними интерференционными максимумами или минимумами, интерференционные порядки которых отличаются на единицу. Для рассматриваемой интерференционной картины двух источников волн одинаковой интенсивности в соответствии с выражениями (4.9) ширина полосы   оказывается равной:

.

(4.10)

Из этой формулы следует, что расстояние между интерференционными полосами растёт при уменьшении  . Кроме того, если расстояние до экрана соизмеримо с расстоянием между щелями ( ) , то

.

В этом случае для световых волн, длина волны которых   порядка долей микрона, интерференционные полосы неразличимы невооружённым взглядом и для их наблюдения необходимо использовать микроскоп.

Рассмотрим распределение интенсивности света в плоскости интерференционной картины, если интенсивность источников одинаковы, т.е.  . Из выражения (4.4a) в этом случае следует:

,

(4.11)

где   - волновое число электромагнитных волн в вакууме,   - оптическая разность хода волн от источников до точки наблюдения, равная   в соответствии с выражением (4.7).

Рис. 4.3b.

В плоскости экрана интенсивность интерференционной картины (рис. 4.3b) двух точечных монохроматических источников электромагнитных волн одинаковой интенсивности   меняется в зависимости от координаты   точки наблюдения на экране в соответствии с выражением, следующим из (4.4a)

.

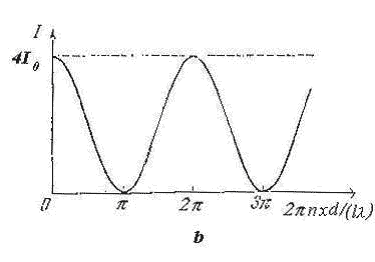
Изменение интенсивности в соответствии с этим выражением в оптике известно, как изменение интенсивности по закону "квадрат косинуса". В максимумах интенсивность интерференционной картины в четыре раза превышает интенсивность интерферирующих источников волны. В минимумах интенсивность равна нулю. Среднее значение распределения интенсивности   на интерференционной картине равно сумме интенсивностей каждого из интерферирующих источников. На рис. 4.3c приводится фотография распределения интенсивности интерференционной картины от двух щелей. Полутона, видные на фотографии, соответствуют изменению интенсивности по закону 'квадрат косинуса '.

Для немонохроматических источников электромагнитных волн в центре картины максимумы всех составляющих колебаний разных частот интерферирующих источников совпадают. Однако, по мере удаления от центра ввиду того, что направления на максимумы и минимумы зависят от длины волны, может происходить ' наложение' интерференционных максимумов одной волны на минимумы другой. В результате

Рис. 4.3c.

интерференционная картина немонохроматических источников будет смазываться ближе к краю их интерференционного поля. Следовательно,число наблюдаемых интерференционных полос будет меньше по сравнению со случаем монохроматических источников. Возможность наблюдения интерференционной картины электромагнитных волн обусловлена свойством когерентности их источников.