
- •Прямое и обратное преобразование z-преобразование.
- •Обратное z-преобразование
- •6. Свёртка дискретных функций.
- •7. Методы численного интегрирования. Метод прямоугольников.
- •8. Методы численного интегрирования. Метод трапеций.
- •9. Методы численного интегрирования. Метод Симпсона.
- •10. Интегральные оценки качества переходных процессов.
8. Методы численного интегрирования. Метод трапеций.
Существует множество методов приближенного вычисления одномерных интегралов. Сначала строятся простейшие формулы для приближенного вычисления интегралов по отрезку. Такие формулы называются квадратурными. Повышение точности вычисления интегралов осуществляется за счет повышения порядка точности квадратур, за счет разбиения отрезка на части, за счет сведения интегралов от функций с «особенностями» к интегралам от более гладких функций.
Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции.
Ставится задача вычислить интеграл вида
 (6.1)
(6.1)
где
 и
и
 – нижний и верхний пределы интегрирования;
– нижний и верхний пределы интегрирования;
– непрерывная
функция на отрезке

К численному интегрированию обращаются, когда нельзя через элементарные функции аналитически записать первообразную интеграла (6.1) или когда подобная запись имеет сложный вид.
Сущность
метода трапеций состоит в замене
подынтегральной функции на участке
полиномом первой степени
 .
Такая аппроксимация неоднозначна. Одним
из возможных способов является проведение
прямой через значения функции на границах
интервала интегрирования (рис. 6.4). В
этом случае приближенное значение
интеграла определяется площадью трапеции
.
Такая аппроксимация неоднозначна. Одним
из возможных способов является проведение
прямой через значения функции на границах
интервала интегрирования (рис. 6.4). В
этом случае приближенное значение
интеграла определяется площадью трапеции
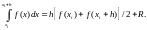 (6.20)
(6.20)
Априорную
погрешность
метода трапеций получим путем
интегрирования тейлоровского разложения
подынтегральной функции около точки

 (6.21)
(6.21)
и интеграл
 (6.22)
(6.22)
С
помощью разложения (6.21) вычислим
подынтегральную функцию в точке


откуда
 (6.23)
(6.23)
Подставляя произведение (6.23) в выражение (6.22), получим

Следовательно, главный член погрешности метода трапеций на одном интервале будет
 (6.24)
(6.24)
Если интегрирование проводится путем разбиения отрезка на несколько интервалов, то общую площадь получим суммированием частных погрешностей (6.24)
 (6.25)
(6.25)

Рис. 6.4. Метод трапеций
Получили, на первый взгляд, неожиданный результат, что метод трапеций имеет погрешность в два раза больше по абсолютной величине по сравнению с методом средних прямоугольников, хотя аппроксимация подынтегральной функции проводилась полиномом первой, а не нулевой степени. По-видимому, выбранный вариант аппроксимации подынтегральной функции прямой, проходящей через ее значения на границах, не является оптимальным. Задача выбора способа аппроксимации полиномом заданной степени с наименьшей возможной погрешностью была решена Гауссом, что привело к развитию целого класса методов.
Как видно из выражения (6.25), метод трапеций имеет второй порядок. Если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка применять метод средних прямоугольников вследствие его меньшей погрешности.
