Перша космічна швидкість

• Швидкість, яку необхідно надати тілу, щоб воно стало штучним супутником планети

Д руга і третя космічні швидкості

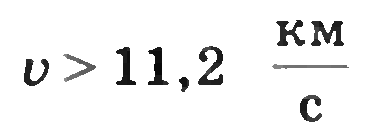
Си́ла іне́рції — фіктивна сила, яку вводять для опису динаміки механічного руху в неінерційних системах відліку.

,

де   — сила інерції, m — маса,   — прискорення, з яким рухається система координат.

У системі, що обертається довкола осі, сила інерції набирає вигляд:

 ,

де   кутова швидкість, а v швидкість об'єкта в системі, що обертається. Перший доданок у формулі (1) називається силою Коріоліса, ця сила перпендикулярна до швидкості. Другий доданок — це відцентрова сила, а третій враховує кутове прискорення неінерційної системи координат.

Поступальний рух – це такий рух, при якому будь-яка пряма, що проведена через дві довільні точки тіла, залишається паралельною сама до себе. При поступальному русі траєкторії всіх точок тіла однакові.

При поступальному русі мірою інертних властивостей матеріальної точки (тіла) є маса, а при обертовому русі її аналогом буде момент інерції, який рівний добутку маси матеріальної точки на квадрат віддалі до центра або осі обертання

.

1 . Сили інерції при прискореному поступальному русі систем відліку.

На дні кабіни ліфту знаходиться деяке тіло.

Нехай ліфт опускається вниз з прискоренням . Система відліку зв’язану з поверхнею Землі, нехтуючи її добовим обертанням, будемо вважати інерціальною. За другим законом Ньютона

. (1.78)

Система відліку зв’язану з ліфтом є неінерціальною. В системі тіло

перебуває в стані спокою, тобто . Згідно (1.77)

. (1.79)

Із порівняння (1.78) і (1.79) маємо, що .

В проекції на вісь рівняння дає Вага тіла чисельно дорівнює .

Тоді .

Якщо ліфт нерухомий, то і вага тіла . У ліфті, що прискорено опускається вниз, вага тіла частково компенсується силою інерції.

При сила інерції і повністю компенсує вагу тіла . Такий стан називається станом “невагомості”.

Принцип д'Аламбера —Лагранжа або динамічний принцип віртуальних переміщень стверджує, що для того, щоб рівняння рухуматеріальних точок у механічній системі з накладеними зв'язками зводилися до форми

,

де   — маси матеріальних точок,   — сили, які на них діють, а   — сили реакції, необхідно й достатньою, щоб робота всіх сил, включаючи сили інерції на будь-яких віртуальних переміщеннях дорівнювала нулю.

Зв'язки, які задовольняють такій умові називаються ідеальними зв'язками.

Тема 2. Статика

Виділяють три види рівноваги:

1. Сталий - тіло при малому відхиленні від положення рівноваги повертається в це положення

2. Нестійкий - тіло при малому відхиленні від положення рівноваги йде від цього положення

3. Байдуже - тіло при малому відхиленні від положення рівноваги виявляється в новому положенні рівноваги

Умова рівноваги

Тверде тіло перебуває в рівновазі якщо сума всіх сил, прикладених до даного тіла, і їх моментів дорівнюють нулю. Або, що теж саме, головний вектор і головний момент системи сил, прикладених до тіла, дорівнюють нулю.

Для запису умови рівноваги системи, що складається з твердих тіл, систему поділяють на окремі частини, і записують рівняння рівноваги як для всієї системи, так і для її частин. При цьому можливі кілька варіантів запису еквівалентних умов рівноваги в залежності від вибору частин системи, для яких записуються рівняння.