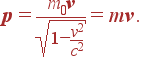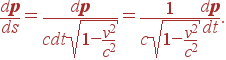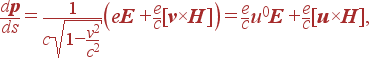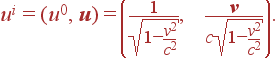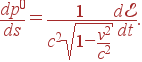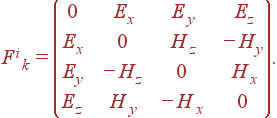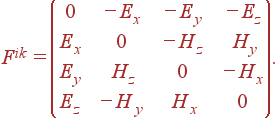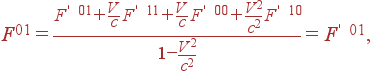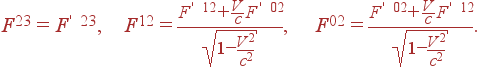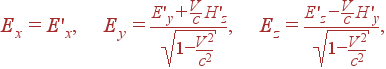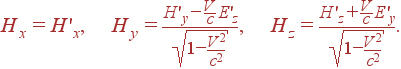Лекция 7

• Сила Лоренца.

• Релятивистская форма уравнений движения.

• Тензор электромагнитного поля.

• Преобразования Лоренца для электрического и магнитного поля.

• Инварианты поля.

Сила Лоренца

Сила, действующая на заряженную частицу в электрическом и магнитном поле в некоторой инерциальной системе K, называется силой Лоренца и записывается в виде

(1)

где e — заряд частицы, v — её скорость. Это выражение можно также считать определением электрического и магнитного полей в системе K. С помощью этой формулы уравнение движения частицы в поле в нерелятивистской механике можно записать в виде:

(2)

Релятивистская форма уравнений движения

Наша задача сейчас — записать это уравнение, как говорят, в ковариантной форме, в которой оно было бы справедливо в любой инерциальной системе отсчета, т.е. представляло бы собой равенство двух 4-векторов. Первое, что надо сделать для перехода в релятивистскую область, это считать p в этом уравнении пространственной компонентой 4-импульса:

(3)

Или, что то же самое, считать массу частицы, зависящей от её скорости обычным образом.

Оказывается, что этого изменения достаточно для того, чтобы это уравнение описывало и движение частиц со скоростями, близкими к скорости света. Конструкторы современных ускорителей при своих расчетах опираются именно на это уравнение. На этом можно было бы поставить точку. Но постойте, скажете вы. Ведь величина dp/dt не представляет собой пространственной компоненты какого-либо 4-вектора. А про правую часть мы вообще ничего не можем сказать, т.е. не знаем, как преобразуются поля E и H при переходе к другой инерциальной системе отсчета.

Поэтому давайте попытаемся представить это уравнение как равенство двух 4-векторов. Мы увидим, что эта затея принесет нам много интересной и полезной информации и позволит сделать важные выводы о единстве и различие электрического и магнитного полей. Разберемся для этого сначала с левой частью. Итак, dp/dt нас не устраивает. Исходя из имеющегося у нас опыта было бы лучше иметь вместо этого dp/ds. Тогда это будет пространственная компонента некоторого 4-вектора, поскольку — это скалярная величина в геометрии Минковского. Таким образом,

(4)

Величину dp/dt в этом равенстве можно заменить на силу Лоренца. Тогда получим

(5)

где мы ввели в игру 4-скорость

(6)

Таким образом, слева у нас стоит пространственная компонента 4-вектора. Значит, справа тоже. Её можно считать пространственной компонентой 4-силы f. Интересной особенностью этой величины является то, что она, как следует из выражения (5), — линейна по 4-скорости частицы uⁱ. А линейная связь между двумя 4-векторами всегда может быть представлена в виде тензорного равенства

(7)

где коэффициенты пропорциональности представляют собой компоненты 4-тензора II ранга Fⁱ  _k.  ¹

Тензор электромагнитного поля

В такой форме эти компоненты зависят только от проекций электрического и магнитного поля E и H. Давайте найдем эти компоненты! Исходить будем из условия, что ковариантная форма уравнений движения имеет вид:

(8)

(мы убедились в этом для значений i = 1,2,3, соответствующих пространственным компонентам). Так, с одной стороны

(9)

С другой стороны из уравнение (5)

(10)

С учетом, что u_y≡ u^z, а u_z≡ u³ и сравнивая уравнения (9) и (10), получаем

F1  0 = Ex ,     F1  1 = 0 ,     F1  2 = Hz ,      F1  3 = –Hy  .

(11)

Аналогичным образом, сравнивая проекции на оси y и z уравнений (5) и (8), получаем две дополнительных цепочки равенств

F2  0 = Ey ,     F2  1 = –Hz ,     F2  2 = 0 ,      F2  3 = Hx ,

(12)

F3  0 = Ez ,     F3  1 = Hy ,     F3  2 = –Hx ,      F3  3 = 0 .

(13)

Таким образом, у нас есть выражения для всех компонент тензора Fⁱ  _k, за исключением 4-х компонент F⁰  ₀, F⁰  ₁, F⁰  ₂ и F⁰  ₃.

Найдем эти компоненты, воспользовавшись законом сохранения энергии. Поскольку временная компонента 4-импульса , то

(14)

С другой стороны,

(15)

т.е. изменение энергии частицы в единицу времени равно работе силы в единицу времени. Член с магнитным полем вклада не дает, поскольку v·[v×H] = 0, т.е. магнитное поле работу над частицей не производит. Поэтому

(16)

Сравнивая это с (8)

(17)

находим недостающие 4 компоненты

F0  0 = 0 ,      F0  1 = Ex ,     F0  2 = Ey ,       F0  3 = Ez  .

(18)

В итоге тензор Fⁱ  _k можно представить в виде

(19)

Наиболее употребительная запись этого тензора через контрвариантные компоненты. Поднимая по известному правилу 2-ой индекс, получим

(20)

Этот антисимметричный 4-тензор II ранга называется тензором электромагнитного поля. С его помощью уравнение движения можно представить в ковариантном виде

(21)

Таким образом, мы видим, что требование ковариантности уравнений движения  ² приводит нас к выводу о том, что электрическое и магнитное поле являются компонентами антисимметричного 4-тензора II ранга F^ik. Можно сказать, что этот результат демонстрирует единство электрического и магнитного полей.

Можно спросить: ну, а какая от этого польза? Польза довольно очевидна. Зная, как преобразуются компоненты 4-тензора при переходе от одной инерциальной системы отсчета к другой, мы можем вывести отсюда формулы преобразования для электрического и магнитного полей, связывающие эти величины в разных инерциальных системах отсчета.

Преобразования Лоренца для электрического и магнитного поля

Рассмотрим, как и ранее, две системы отсчета K и K' с параллельными осями координат, причем система K' движется со скоростью V в положительном направлении вдоль оси x. В лекции 20 мы вывели формулу (26) для преобразования компоненты произвольного тензора II ранга A⁰¹. Воспользовавшись ей, находим закон преобразования компоненты F⁰¹

(22)

т.е. эта компонента не меняется. При выводе мы пртняли во внимание факт антисимметричности тензора F^ik, а именно то, что F^'  11 = F^'  00 = 0, и F^'  10 = –F^{'  01}.

Теперь заметим, что поскольку координаты x² и x³ не меняются, то не меняется и компонента тензора F²³ (она преобразуется так же, как произведение x²x³). По той же причине компоненты F¹², F¹³ и F⁰², F⁰³ преобразуются соответственно как x¹ и x⁰:

(23)

И аналогично для компонент F¹³ и F⁰³.

В результате, переписывая это в компонентах тензора F^ik (20), получим преобразования Лоренца для электрического и магнитного полей E и H:

(24)

(25)

Таким образом, электрическое и магнитное поля, как и большинство физических величин, — относительны, т.е. их величина (и направление) различаются в разных системах отсчета. В частности, электрическое (или магнитное) поле может быть равно нулю в одной системе отсчета и в то же время присутствовать в другой системе. Например, покоящийся электрический заряд создает вокруг себя одно только электрическое поле. Однако, рассматривая этот заряд в движущейся (относительно заряда) системе отсчета, мы замечаем, что поскольку движущийся заряд эквивалентен току, то вокруг него, помимо электрического, должно быть еще и магнитное поле. Это, как мы знаем, действительно имеет место.

Инварианты поля

Пользуясь преобразованиями Лоренца для полей, легко убедиться непосредственно, что имеются две комбинации (квадратичные по полю), инвариантные к преобразованиям от одной инерциальной системы отсчета к другой. Эти инварианты имеют вид

(26)

причем второй инвариант является псевдоскаляром (в нашем обычном 3-х мерном пространстве).

Из инвариантности этих выражений вытекает следующее. Так, если в какой-нибудь системе отсчета вектора E и H перпендикулярны друг другу, т.е. E·H = 0, то они будут перпендикулярны и во всякой другой системе отсчета. Если в какой-нибудь системе отсчета абсолютные значения векторов E и H равны друг другу (E²–H² = 0), то они будут одинаковы и в любой другой системе.

¹ Для удобства мы выделили из этого тензора множитель e/c.

² Согласно специальной (и общей) теории относительности все законы природы должны выражаться в ковариантной форме.

83