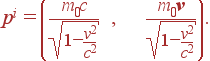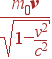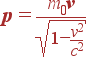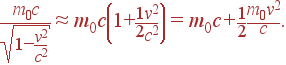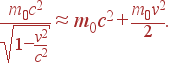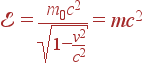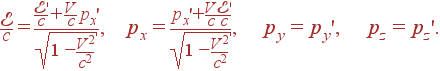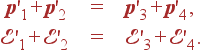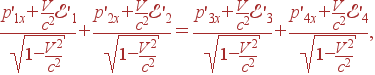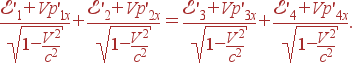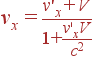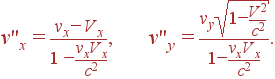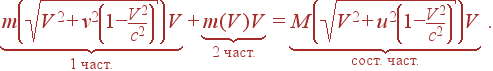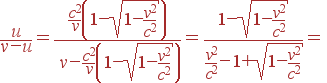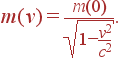Лекция 5

• Релятивистский импульс. 4-вектор энергии-импульса.

• Закон сохранения энергии-импульса.

• Зависимость массы от скорости. Связь энергии с массой.

• Формула Эйнштейна .

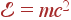Релятивистский импульс. 4-вектор энергии-импульса.

По аналогии с 4-скоростью uⁱ введем 4-импульс для свободной частицы

pi = m0cui ,

(1)

где m₀ — масса в системе покоя частицы (масса покоя), или в компонентах

(2)

Пространственная компонента 4-импульса

(3)

в пределе c→∞ переходит в обычный (классический) импульс p = m₀v. Поэтому мы, по аналогии с классической механикой, будем называть величину

(4)

релятивистским импульсом. Этому выражению можно придать обычный для классической механики вид

(5)

есть масса частицы, зависящая от ее скорости.

Выясним теперь, что представляет из себя временная компонента 4-импульса — . Для этого посмотрим, во что переходит это выражение при v<< c. Разлагая функцию в ряд Тейлора по малому параметру v/c, мы имеем  ¹

(6)

Умножая это выражение на c, получим

(7)

Первое слагаемое в правой части этой формулы есть некоторая константа, не зависящая от скорости частицы и имеющая размерность энергии, а второе — есть не что иное, как кинетическая энергия частицы в классической механике. Поэтому по аналогии с классической механикой величина

(8)

называется энергией частицы в релятивистской механике, а энергия частицы при v = 0, т.е. величина m₀c² называется энергией покоя.

После этих определений можно представить 4-импульс частицы в виде

(9)

т.е. временная компонента 4-импульса представляет собой энергию частицы, деленную на скорость света c, а пространственная — импульс частицы. Поэтому часто 4-импульс называют 4-вектором энергии-импульса. Вспомнив о том, что 4-скорость является "единичным" 4-вектором, т.е. uⁱu_i = 1, мы получаем следующее релятивистски инвариантное соотношение:

pipi = m02c2 ,

(10)

или

(11)

которое справедливо независимо от выбора инерциальной системы отсчета. В другой системе отсчета K' имеет место такое же соотношение

(12)

Иными словами, полученная формула Лоренца инвариантна.

Сами и p меняются при переходе к другой системе отсчета в соответствии с преобразованиями Лоренца для 4-векторов

(13)

Домножая первое соотношение на c, получим

(14)

Закон сохранения энергии-импульса

Какой смысл во всех этих обозначениях, определениях и названиях? Ведь если исходить только из совпадения данной величины с ее классическим пределом при c→∞, то мы могли бы назвать, например, "импульсом" величину

(15)

(она переходит в классическое выражение при c→∞), а "энергией" величину

(16)

(второе слагаемое в этой формуле есть кинетическая энергия частицы в классической механике).

Однако можно показать, что эти величины не являются компонентами какого-либо 4-вектора. А почему нам надо, чтобы они были компонентами 4-вектора? Все дело в том, что в релятивистской физике, так же как и в физике нерелятивистской, выполняются законы сохранения импульса и энергии. Это есть, можно сказать, опытный факт. Не обнаружено пока отклонений от этих законов сохранения.  ² Но в силу принципа относительности эти законы сохранения должны выполняться во всех инерциальных системах, движущихся друг относительно друга равномерно и прямолинейно.

Рис. 1. Столкновение 2-х частиц в лабораторной системе.

Рассмотрим, например, столкновение 2-х частиц в лабораторной системе с образованием двух (вообще говоря, других) частиц. Закон сохранения импульса гласит

p1 + p2 = p3 + p4 .

(17)

А закон сохранения энергии

(18)

Но такие же законы сохранения должны выполняться и в любой другой инерциальной системе K', движущейся относительно лабораторной системы со скоростью V

(19)

Если величины и p являются компонентами 4-вектора, то это следует автоматически из преобразований Лоренца. Например, в проекции на ось x

(20)

Применяя преобразования Лоренца, получаем из (20)

(21)

(22)

После сокращения на имеем

(23)

Домножая второе уравнение на V/c² и вычитая его из первого, получим

(1–V2/c2)(p'1x+p'2x) = (1–V2/c2)(p'3x+p'4x) .

(24)

В итоге мы приходим к закону сохранения импульса в системе K'

p'1x+p'2x = p'3x+p'4x .

(25)

Но если выполняется закон сохранения импульса, то из первого уравнения системы (23) следует закон сохранения энергии

(26)

Таким образом, мы приходим к выводу, что

сохраняющиеся величины в релятивистской физике должны быть компонентами 4-векторов (или тензоров).

Тогда законы сохранения, будучи справедливы в одной инерциальной системе отсчета, будут справедливы и в любой другой инерциальной системе.

Зависимость массы от скорости

Возможно, кто-то остался неудовлетворенным этим довольно формальным выводом выражений для энергии и импульса релятивистской частицы. Поэтому приведем еще один вывод, заимствованный из книги М.Борна "Эйнштейновская теория относительности", Мир, Москва, 1972 г. (стр. 262). Давайте будем искать выражение для импульса частицы в виде

p = m(v)v,

(27)

считая, что масса частицы m(v) есть некоторая функция ее скорости, которую нам предстоит определить исходя из предположения, что импульс частицы — сохраняющаяся величина.

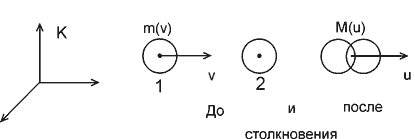
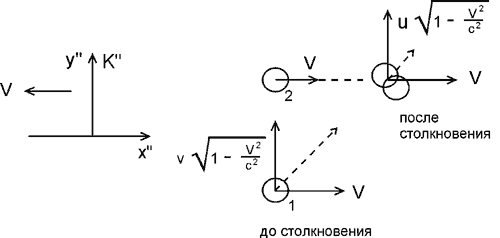
Рассмотрим для этого неупругое столкновение двух одинаковых тел одно из которых покоится (в некоторой лабораторной системе отсчета K), а другое движется к нему со скоростью v. После столкновения тела слипаются и продолжают движение вместе с некоторой скоростью u, которую нам надо найти.

Рис. 2. Неупругое столкновение двух одинаковых тел.

Закон сохранения импульса в проекции на первоначальное направления движения (которое мы выбираем качестве оси x) в лабораторной системе гласит

m(v)v = M(u)u ,

(28)

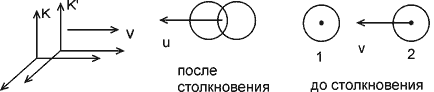
где M(u) — масса образовавшегося тела. Посмотрим теперь на то же столкновение из другой инерциальной системы K', которая движется вправо относительно системы K со скоростью v (рис. 3).

Рис. 3. То же столкновение в системе K'.

В этой системе первая частица покоится, а вторая налетает на нее со скоростью –v. В результате образующаяся составная частица движется со скоростью –u (так как процесс симметрично выглядит в этой системе по сравнению с системой K). Применяя теперь закон сложения скоростей, мы можем связать u и v. Для этого в формулу

(29)

подставим v_x = u, v'_x = –u и V = v. В результате получим

(30)

Относительно скорости u это есть квадратное уравнение. Выбирая из двух корней тот корень, который соответствует скорости, меньшей скорости света, получим

(31)

В пределе c→∞ это переходит в известный классический предел u = v/2.

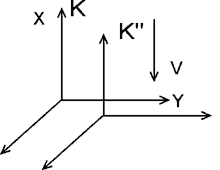
Рассмотрим теперь то же столкновение из системы K'', которая движется вниз со скоростью V.

Рис. 4. Система K''.

В этой системе отсчета, если мы развернем картинку и снова сделаем ось x горизонтальной, столкновение тел будет выглядеть так, как показано на рис 5.

Рис. 5. Столкновение в системе K''.

Для определения компонент скоростей тел до и после столкновения в системе K'' воспользуемся формулами преобразования скоростей

(32)

В данном случае

Vx = –V

(33)

и

v1x = v2x = vσ x = 0

(34)

(значок σ относится к телу образовавшемуся в результате столкновения). Поэтому из формул (32) следует для x компонент скоростей в системе K''

v''1x = v''2x = v''σ x = V.

(35)

Аналогичным образом, поскольку

v1y = v,      v2y = 0,      vσ y = u ,

(36)

получаем для y компонент скоростей

(37)

Запишем теперь закон сохранения импульса в системе K'' в проекции на ось x

Сокращая на V, получаем

(38)

Это равенство должно выполняться при любом V, в том числе и при V = 0

m(0)+m(v) = M(u) .

(39)

В таком виде оно представляет собой не что иное, как закон сохранения массы при неупругом столкновении двух тел. Подставляя теперь M(u) в закон сохранения импульса (28), получим

(40)

Разрешая это уравнение относительно m(v), приходим к соотношению

(41)

Нам теперь осталось вычислить только отношение u/(v–u). Подставляя в него скорость u из уравнения (31), получим

			(42)

Таким образом, мы приходим к уже известному нам выражению для массы тела, зависящей от его скорости

(43)

Попутно мы доказали, что если сохраняется импульс (во всех инерциальных системах отсчета), то сохраняется и масса (зависящая от скорости), или, что то же самое, энергия, равная произведению массы тела на квадрат скорости света.

Связь энергии с массой. Формула Эйнштейна

Важнейший результат специальной теории относительности относится к понятию массы. В дорелятивистской физике было два закона сохранения: закон сохранения массы и закон сохранения энергии. Оба этих фундаментальных закона считались совершенно независимыми друг от друга. Теория относительности объединила их в один. Так, если тело, движущееся со скоростью v и получающее энергию E₀ в форме излучения  ³ без изменения своей скорости, увеличивает при этом свою энергию на величину

(44)

В результате полная энергия тела становится равной

(45)

Следовательно, тело обладает такой же энергией, как и тело, движущееся со скоростью v и имеющее массу покоя m₀+E₀/c². Таким образом, можно сказать, что если тело получает энергию E₀, то его масса покоя увеличивается на величину E₀/c². Так, например, нагретое тело имеет большую массу, чем холодное, и, если бы в нашем распоряжении были бы очень точные весы, мы бы убедились в этом непосредственно с помощью взвешивания.

Однако в нерелятивистской физике изменения энергии E₀, которые мы могли сообщить телу, были, как правило, недостаточно велики, чтобы можно было заметить изменения инертной массы тела. Величина E₀/c² в нашей обыденной жизни слишком мала по сравнению с массой покоя m₀, которую имело тело до изменения энергии. Этим обстоятельством объясняется тот факт, что закон сохранения массы так долго имел в физике самостоятельное значение.

Совершенно по-другому обстоит дело в релятивистской физике. Хорошо известно, что с помощью ускорителей мы можем сообщить телам (элементарным частицам) огромную энергию, достаточную для рождения новых (элементарных) частиц — процесс, который наблюдается сейчас сплошь и рядом на современных ускорителях элементарных частиц. Формула Эйнштейна "работает" в ядерных реакторах атомных электростанций, где энергия высвобождается за счет процесса деления ядер тяжелых элементов. Масса конечных продуктов реакции меньше массы исходного вещества. Эта разница масс, деленная на квадрат скорости света, и представляет собой полезную высвобожденную энергию. Подобным же образом нас обеспечивает теплом и наше Солнце, где за счет реакции термоядерного синтеза водород превращается в гелий и выделяется огромное количество энергии.

Сейчас можно считать твердо установленным, что инертная масса тела определяется количеством запасенной в теле энергии. Эту энергию сполна можно получить в процессе аннигиляции вещества с антивеществом, например, электрона с позитроном. В результате такой реакции образуются два гамма-кванта — фотона очень большой энергии. Этот источник энергии, возможно, будет использоваться в будущем в фотонных двигателях ракет для достижения ими субсветовых скоростей при полетах к далеким галактикам.

¹ Поскольку при x<< 1

² Когда такие отклонения обнаруживаются, то в конце концов оказывается, что это либо ошибка, либо, если выясняется, что ошибки нет, это приводит к открытию новых элементарных частиц. Наиболее яркий пример такого рода — это открытие нейтрино.

³ Здесь E₀ — полученная телом энергия при наблюдении из системы координат, движущейся вместе с телом.