5. Движение тела, брошенного горизонтально. Вывод формулы траектории движения, вывод формул для времени падения и дальности полета

Н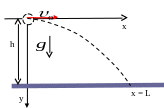 аправим координатную ось OY вертикально вниз, совместив начало координат с местом начала падения, тогда поверхность Земли имеет координату .

В горизонтальном направлении никакие силы на тело не действуют, поэтому горизонтальная составляющая скорости не меняется. По вертикали скорость тела изменяет сила тяжести, т.е. тело движется с постоянным ускорением , направленным вертикально вниз. Скорость тела в проекции на выбранные оси изменяется по закону: и . Координаты: 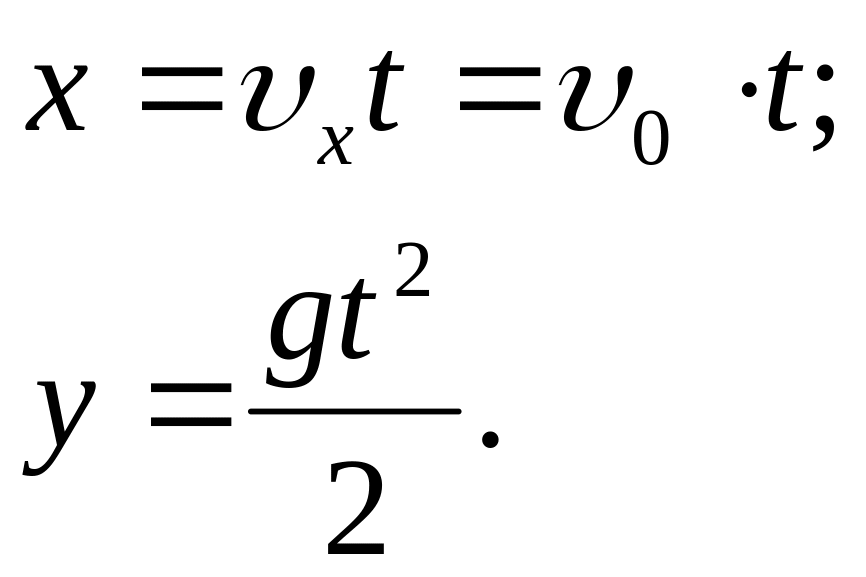Если исключить из этих уравнений время движения - получили уравнение траектории – ветвь параболы.

Вдоль оси у тело свободно падает. В момент падения - время свободного падения определяется высотой с которой падает тело.

Скорость тела в момент падения может быть определена из закона сохранения энергии: .

Дальность полета тела по горизонтали - зависит от высоты и начальной скорости тела.

При движении по криволинейной траектории скорости направлена по касательной к траектории.

6. Движение тела по окружности с постоянной по модулю скоростью. Угловая скорость, угол поворота, период обращения, частота. Связь между угловой и линейной скоростью.

Д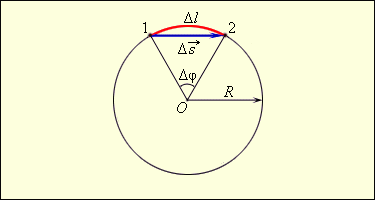 вижение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения   удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис.). Длина дуги связана с углом поворота соотношением  Δl = R Δφ. При малых углах поворота Δl ≈ Δs.

Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δt → 0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:  . Угловая скорость измеряется в рад/с. Связь между модулем линейной скорости υ и угловой скоростью ω:  υ = ωR

При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора скорости.

Каждый оборот тело совершает за один и тот же промежуток времени – период Т (время одного оборота). Число оборотов за 1 с называется частотой [об/с]. Частота оказывается величиной обратной периоду.

Из определения скорости .

Из определения угловой скорости

Равномерное движение тела по окружности является движением с ускорением. Ускорение направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной  υ  и угловой ω скоростями соотношениями: 

При малых углах Δφ направление вектора  приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δt → 0. При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.