3. Движение тела, брошенного вертикально вверх, вертикально вниз. Вывод формулы для времени движения тела брошенного вертикально с высоты h.

Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте). В конце XVI века знаменитый итальянский ученый Г. Галилей опытным путем с доступной для того времени точностью установил, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же. До этого в течение почти двух тысяч лет, начиная с Аристотеля, в науке было принято считать, что тяжелые тела падают на Землю быстрее легких.

Ускорение, с которым падают на Землю тела, называется ускорением свободного падения. Вектор ускорения свободного падения обозначается символом   он направлен по вертикали вниз. В различных точках земного шара в зависимости от географической широты и высоты над уровнем моря числовое значение g оказывается неодинаковым, изменяясь примерно от 9,83 м/с² на полюсах до 9,78 м/с² на экваторе. Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с² или даже 10 м/с².

А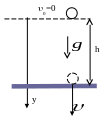 . Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости. Свободное падение является прямолинейным движением с постоянным ускорением.

Если направить координатную ось OY вертикально вниз, совместив начало координат с местом начала падения, тогда поверхность Земли имеет координату .

Скорость тела в проекции на выбранную ось изменяется по закону , координата .

В момент падения - время свободного падения определяется высотой с которой падает тело.

Скорость тела в момент падения: - так же однозначно определяется высотой, с которой упало тело.

Б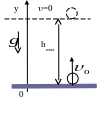 . Движение тела брошенного вертикально вверх с некоторой начальной скоростью.

Направим координатную ось OY вертикально вверх, совместив начало координат с точкой бросания.

Скорость тела в проекции на выбранную ось изменяется по закону , координата .

В верхней точке траектории - время подъема определяется начальной скоростью тела. Если пренебречь сопротивлением воздуха, то время падения и время подъема будут равны. Т.е. время движения (до поверхности земли) .

Из уравнения зависимости координаты от времени максимальная высота подъема . Из верхней точки траектории тело падает свободно. Скорость тела в момент падения на землю равна начальной скорости. Скорость тела на высоте h < h_max можно найти из уравнения соответствующего закону сохранения энергии.

4. Движение тела брошенного под углом к горизонту. Вывод формул дальности полета, максимальной высоты подъема, времени движения

Н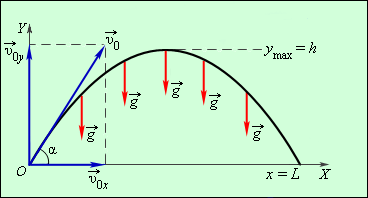 аправим координатную ось OY вертикально вверх, совместив начало координат с точкой бросания.

В горизонтальном направлении никакие силы на тело не действуют, поэтому горизонтальная составляющая скорости не меняется. По вертикали скорость тела изменяет сила тяжести, т.е. тело движется с постоянным ускорением , направленным вертикально вниз. Скорость тела в проекции на выбранные оси изменяется по закону: и . Из рисунка: и .

Координаты:

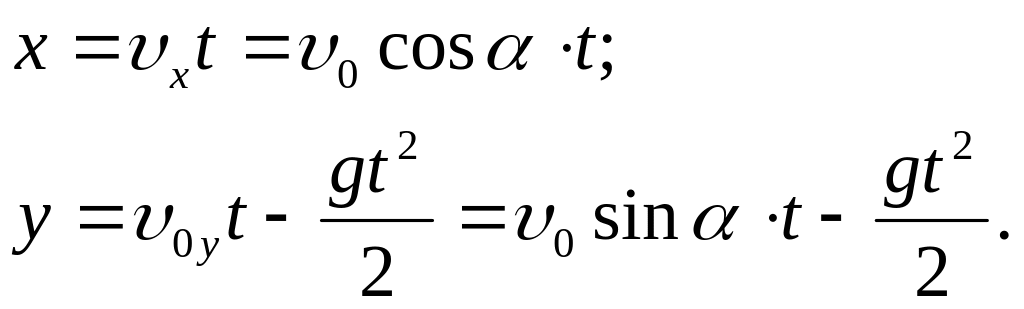
В верхней точке траектории - время подъема определяется вертикальной составляющей начальной скорости тела. Если пренебречь сопротивлением воздуха, то время падения и время подъема будут равны. Т.е. время движения (до поверхности земли) .

Из уравнения зависимости координаты от времени максимальная высота подъема . Скорость тела в момент падения на землю равна по модулю начальной скорости, но проекция скорости на ось у меняет знак на противоположный. Скорость тела на высоте h < h_max можно найти из уравнения соответствующего закону сохранения энергии.

Дальность полета по горизонтали .

Из приведенных формул следует, что дальность полета будет максимальной для угла 45