2. Относительность механического движения. Вывод формулы закона сложения скоростей. Относительная скорость

В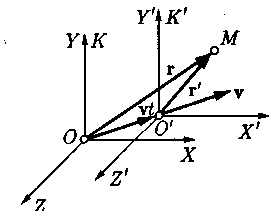 ньютоновской механике при переходе от одной инерциальной системы отсчета К(х, у, z, t) к другой К^/(х^/, у^/, z^/, t^/), движущейся относительно К поступательно с постоянной скоростью , пользуются преобразованиями координат и времени, которые называются преобразованиями Галилея. Они основаны на двух аксиомах об инвариантности (неизменности) промежутков времени и расстояний. Из первой аксиомы следует, что ход времени одинаков во всех системах отсчета, а из второй — что размеры тела не зависят от скорости его движения.

Е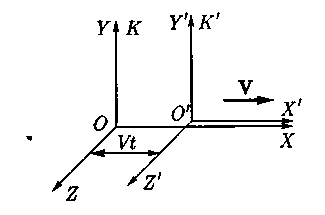 сли сходственные оси декартовых координат инерциальных систем отсчета К и К проведены попарно параллельно друг другу и если в начальный момент времени (t = t^/ = 0) начала координат O и O^/ совпадают друг с другом (рис.), то преобразования Галилея имеют вид

или и

Обычно оси координат проводят так, чтобы система К^/ двигалась вдоль положительного направления оси ОХ (рис.). В этом случае преобразования Галилея имеют наиболее простой вид:

Из преобразований Галилея вытекает следующий закон преобразования скорости произвольной точки М при переходе от одной инерциальной системы отсчета К (скорость точки ) к другой К^/ (скорость той же точки ): - классический закон сложения скоростей (скорость тела относительно неподвижной системы отсчета складывается из скорости тела относительно движущейся системы отсчета и скорости подвижной системы отсчета относительно неподвижной).

Ускорения точки М в системах отсчета К ( ) и К^/ ( ) одинаковы: .

Итак, ускорение материальной точки не зависит от выбора инерциальной системы отсчета — оно инвариантно относительно преобразований Галилея.

Силы взаимодействия материальных точек зависят только от их взаимного расположения и от скоростей движения друг относительно друга. Взаимное расположение каких-либо двух точек 1 и 2 характеризуется вектором, равным разности радиусов-векторов этих точек, т.е. в системе отсчета К вектором _; а в системе К^/ — вектором . Из преобразований Галилея следует, что . Поэтому расстояния между точками 1 и 2 в системах К и К^/ одинаковы.

Скорость движения точки 2 относительно точки 1 равна разности скоростей этих точек: (в системе К) и (в системе К^/). Из преобразований Галилея следует, что .

Итак, взаимное расположение и скорость относительного движения любых двух материальных точек не зависят от выбора инерциальной системы отсчета — они инвариантны относительно преобразований Галилея. Соответственно инвариантны относительно преобразований Галилея и силы, действующие на материальную точку:

Уравнения, выражающие второй и третий законы Ньютона, не меняются относительно преобразований Галилея, т. е. не изменяют свой вид при преобразовании координат и времени от одной инерциальной системы отсчета К к другой К^/: , (в системе К), , (в системе К^/), Где , - масса рассматриваемой материальной точки, одинаковая во всех системах отсчета.

Таким образом, в ньютоновской механике справедлив механический принцип относительности (принцип относительности Галилея): законы механики одинаковы во всех инерциальных системах отсчета.

Это значит, что в разных инерциальных системах отсчета все механические процессы при одних и тех же условиях протекают одинаково. Следовательно, с помощью любых механических экспериментов, проведенных в замкнутой системе тел, нельзя установить, покоится эта система или движется равномерно и прямолинейно (относительно какой-либо инерциальной системы отсчета). Механический принцип относительности свидетельствует о том, что в механике все инерциальные системы отсчета совершенно равноправны. На основе законов механики нельзя выделить из множества инерциальных систем отсчета какую-то «главную» инерциальную систему отсчета, которая обладала бы какими-либо преимуществами перед другими, так что движение тел относительно нее можно было бы рассматривать как их «абсолютное движение», а покой как «абсолютный покой». Понятия покой и движение в механике являются относительным.