14. Сила упругости. Закон Гука. Виды деформаций

М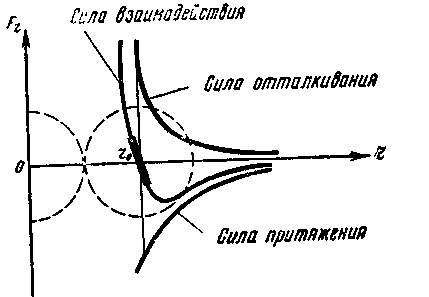 ежду молекулами одновременно действуют и силы притяжения, и силы отталкивания. Силы взаимодействия молекул являются короткодействующими, их действие проявляется лишь на расстояниях, не превышающих нескольких собственных размеров молекулы. Область пространства, в которой проявляется действие молекулярных сил, называют сферой молекулярного действия. Радиус этой сферы равен примерно 10^-9 м. Силы молекулярного взаимодействия зависят от расстояния между молекулами. При этом характер зависимости от расстояния у сил притяжения и сил отталкивания различен. При увеличении расстояния между молекулами силы отталкивания убывают быстрее, чем силы притяжения, а при уменьшении этого расстояния возрастают быстрее, чем силы притяжения. Установлено, что силы взаимодействия молекул обратно пропорциональны n-й степени расстояния г между центрами масс молекул, т. е. F . Для сил притяжения n = 7, а для сил отталкивания n принимает значения от 9 до 15. (Например, для молекулы воды F_пр , a F_от . Сила отталкивания считается положительной, а сила притяжения отрицательной. На рис. изображены графики зависимостей от расстояния между молекулами силы отталкивания (кривая 1), силы притяжения (кривая 2) и результирующей этих сил (кривая 3). Существует такое расстояние между молекулами го, на котором сила притяжения равна силе отталкивания, т. е. их результирующая сила равна нулю. Если расстояние между молекулами r > r₀, преобладают силы их взаимного притяжения, если же r < r₀, преобладают силы отталкивания. Таким образом, результирующая сил молекулярного взаимодействия на больших расстояниях является силой притяжения, а на малых — силой отталкивания. Следовательно, r₀ — это такое равновесное расстояние между молекулами, на котором они находились бы, если бы тепловое движение молекул не нарушало этого равновесия. Описанный характер зависимости сил взаимодействия молекул от их расстояния друг от друга объясняет появление силы упругости при деформации тел. Если под действием внешних сил тело сжимается, расстояние между молекула становится меньше, чем r₀ и появляется сила, препятствующая взаимному сближению молекул. Если же под действием внешних сил тело растягивается, то расстояние r становится больше, чем r₀, и появляется сила, препятствующая взаимному удалению молекул. Вблизи точки r₀ на графике участок кривой 3 является почти прямолинейным, так как при небольшом смещении молекул из положения равновесия силы притяжения или отталкивания между ними возрастают линейно с увеличением смещения. Именно по этой причине при малых деформациях тела (т. е. в пределах его упругости) выполняется закон Гука.

Деформацией называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил.

Деформации, полностью исчезающие после прекращения действия на тело внешних сил, называют упругими, а деформации, сохраняющиеся и после того, как внешние силы перестали, действовать на тело, - пластическими.

Различают деформации растяжения или сжатия (одностороннего или всестороннего), изгиба, кручения и сдвига.

При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации.

Силы, возникающие в теле при его упругой деформации и направленные против направления смещения частиц тела, вызываемого деформацией, называют силами упругости. Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела. Природа упругих сил электрическая.

Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена Гуком. Математическое выражение закона Гука для деформации одностороннего растяжения (сжатия) имеет вид F = kx, где F— сила упругости; х — удлинение (деформация) тела; k — коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью.

Состояние упруго деформированного тела характеризуют величиной , называемой нормальным механическим напряжением. Механическое напряжение равно отношению модуля силы упругости к площади поперечного сечения тела: . Если первоначальная длина нерастянутой проволоки составляла ℓ₀. После приложения силы F проволока растянулась и ее длина стала равной ℓ. Величину ℓ = ℓ - ℓ₀ называют абсолютным удлинением. Величину - относительным удлинением тела. При небольших деформациях нормальное напряжение пропорционально относительному удлинению: , где Е - модуль упругости (модулем Юнга).

Модуль Юнга численно равен такому нормальному напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза (если бы для такой большой деформации выполнялся закон Гука).

Диаграмма растяжения -

э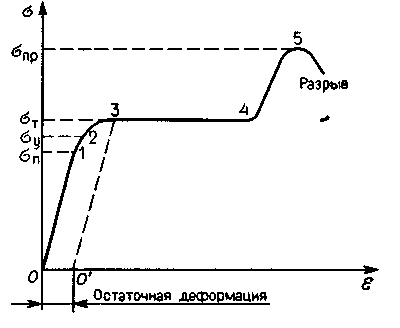 то график зависимости .

На участке 0 – 1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения деформация является упругой и выполняется закон Гука, т. е нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения при котором еще выполняется закон Гука, называют пределом пропорциональности. При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1-2), хотя упругие свойства тела еще сохраняются. Максимальное значение напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности.) Увеличение нагрузки выше предела упругости (участок 2—3) приводит к тому, что деформация становится остаточной. Затем образец начинает удлиняться практически при постоянном напряжении (участок 3—4 графика). Это явление называют текучестью материала. Механическое напряжение при котором остаточная деформация достигает заданного значения, называют пределом текучести. При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинит сопротивляться деформации (участок 4-5 графика). Материалы, у которых область текучести значительна, могут без разрушения выдерживать большие деформации. Такие материалы называют пластичными. Пластичны пластилин, медь, золото. Если же область текучести материала почти отсутствует, он без разрушения может выдержать лишь небольшие деформации. Такие материалы называют хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун. Материал в процессе деформации может упрочняться. В этом можно убедиться при сгибании толстого прута или пластины. Для того чтобы разогнуть образец, требуется заметно большие усилия, чем для его сгибания. Это явление называется наклепом.

Максимальное значение напряжения при превышении которого происходит разрыв образца, называют пределом прочности. После точки 5 кривая идет вниз, это значит, что дальнейшая деформация вплоть до разрыва происходит при все меньшем напряжении.

Коэффициентом безопасности (или запасом прочности) называется отношение предела пропорциональности данного материала максимальному напряжению, которое будет испытывать деталь в работе: . В зависимости от необходимой надежности различных деталей и конструкций коэффициент безопасности выбирают обычно в пределах от 2 до 10.