4.2. Лінійні операції над векторами

Під лінійними операціями над векторами будемо розуміти такі операції як додавання таких відрізків і множення векторів на дійсне число.

Розглянемо кожну із операцій зокрема.

1. Додавання векторів.

Н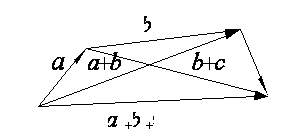 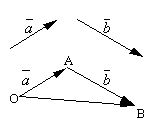ехай і – два довільних вектори. Візьмемо довільну точку O і побудуємо вектор . Після цього з точки A відкладемо вектор . Вектор , що з'єднує початок першого вектора з кінцем другого , називається сумою цих векторів і позначається + = .

С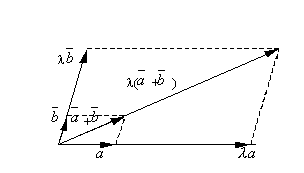 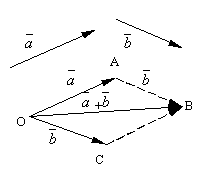формульоване визначення додавання векторів називають правилом паралелограма, тому що ту ж саму суму векторів можна отримати і таким способом. Відкладемо від точки O вектори і . Побудуємо на цих векторах паралелограм ОАВС. Так як вектори , тоді вектор , що є діагоналлю паралелограма, проведеної з вершини O, буде сумою векторів + .

Легко перевірити наступні властивості додавання векторів.

1. Ясно, що додаток нульового вектора до деякого вектора ā не змінює вектора , тобто = = .

2. Додавання векторів комутативне, тобто + = + .

Ц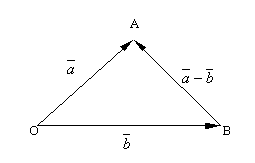 я властивість відразу випливає з правила паралелограма.

3.  Додавання векторів асоціативне, тобто для будь-яких трьох векторів +( + )=( + )+ . Тому суму трьох векторів часто записують просто + + .

Суму трьох векторів можна одержати таким способом. З довільної точки O відкладається вектор, який дорівнює першому вектору. До його кінця приєднується початок другого, до кінця другого – початок третього. Вектор, який з'єднує початок першого вектора з кінцем останнього, буде сумою даних векторів. Аналогічно будується сума будь-якого кінцевого числа векторів.

4. Для будь-якого числа λ і будь-яких векторів і ( + )= + .

Зауважимо, що при множенні векторів на число λ змінюються тільки розміри векторів, тобто масштаб креслення, фігури залишаються подібним. Тому, тому що вектори , і + = утворюють сторони і діагональ паралелограма, то, помноживши всі члени на λ, тобто змінивши лише розміри векторів однаковим чином, ми отримаємо знову паралелограм, а значить, збережеться рівність  + = .

5. Для будь-яких чисел a і b і будь-якого вектора виконується рівність .

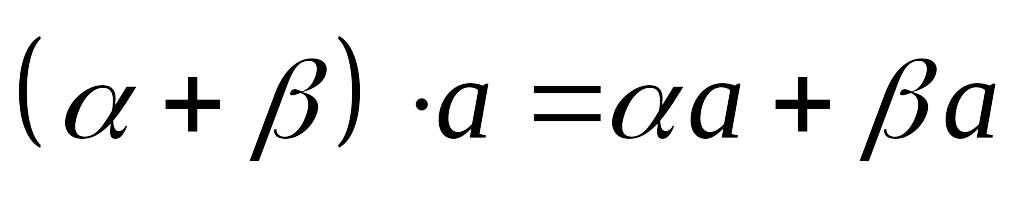Різниця векторів.

Вектор, колінеарний даному вектору , рівний йому по довжині і протилежно напрямлений, називається протилежним вектором для вектора і позначається . Протилежний вектор можна розглядати як результат множення вектора на число λ=–1: .

Різницею двох векторів і називається вектор , дорівнює сумі векторів і , тобто .

Очевидним є те, що , для будь-якого вектора .

Легко показати, що .

Дійсно,

Таким чином, якщо то .

З визначення суми двох векторів випливає правило побудови вектора різниці. Відкладаємо вектори і із загальної точки O. Щоб знайти вектор-різницю, потрібно до додати або вектор . Тоді . Вектор , який з'єднує кінці векторів і і напрямлений від другого вектора до першого, і буде різницею . Дійсно, за правилом додавання або ж векторів .

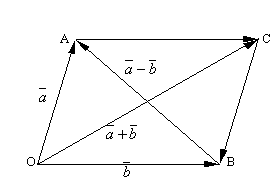
Таким чином, якщо на векторах і , відкладених із загальної точки O, побудувати паралелограм OACB, то вектор , який збігається з однією діагоналлю паралелограма, дорівнює сумі + , а вектор , що збігається з іншою діагоналлю, дорівнює різниці .