
- •Лекція 1-2. Визначники. Визначники другого і третього порядків та їх властивості. Розклад визначника за елементами рядка або стовпця. Поняття про визначники вищих порядків.
- •Визначники. Визначники другого і третього та їх властивості
- •1.2. Розклад визначника за елементами рядка або стовпця
- •1.3. Поняття про визначники вищих порядків
- •Лекція 3-4. Визначення матриці. Дії над матрицями. Обернена матриця. Ранг матриці. Теорема про ранг.
- •2.1. Визначення матриці
- •2.2. Дії над матрицями
- •Властивості додавання:
- •Властивості множення матриці на число:
- •Перемножування матриць
- •2.3. Обернена матриця
- •2.4. Ранг матриці, теорема про ранг.
- •Лекція 5-7. Системи лінійних рівнянь. Розв’язування системи лінійних рівнянь методом Гауса. Правило Крамера. Розв’язок системи лінійних рівнянь за допомогою оберненої матриці.
- •3.1. Системи лінійних рівнянь
- •3.2. Розв’язування систем лінійних рівнянь методом гаусса.
- •3.3. Правило крамера.
- •3.4. Розв’язок системи лінійних рівнянь за допомогою оберненої матриці.
- •Лекція 9-10. Поняття вектора. Лінійні операції над векторами. Скалярний добуток двох векторів. Векторний і мішаний добуток двох векторів.
- •4.1. Поняття вектрора
- •4.2. Лінійні операції над векторами
- •Додавання векторів.
- •Різниця векторів.
- •Множення вектора на число.
- •4.3. Скалярний добуток двох векторів
- •4.4. Векторний і мішаний добуток двох векторів
- •11.1. Системи координат на площині і в просторі.
- •Декартові координати на прямій.
- •11.2. Декартові координати на площині
- •11.3. Декартові координати в просторі
- •11.4. Полярні координати на площині
- •11.5. Циліндричні координати в просторі
- •116. Сферичні координати в просторі
- •5.7. Перетворення декартових координат
- •Паралельне перенесення
- •Поворот навколо початку координат
- •Лекція 12. Пряма на площині. Пряма на площині. Різні види рівнянь прямої на площині. Кут між двома прямими. Відстань від точки до прямої.
- •12.2. Кут між двома прямими, відстань від точки до прямої
- •Лекція 13. Площина у просторі. Площина у просторі. Рівняння площини що проходить через три точки. Кут між двома площинами.. Відстань від точки до площини
- •13.1. Рівняння площини
- •13.2. Кут між площинами, відстань від точки до площини
- •Лекція 14. Пряма у просторі. Пряма у просторі. Кут між двома прямими. Кут між прямою і площиною
- •14.3. Рівняння прямої у просторі
- •14.2. Взаємне розміщення прямої і площини у просторі
- •Лекція 15. Лінії другого порядку.
- •15.1. Криві другого порядку
- •Лекція 16. Лінії другого порядку.
- •16.1. Поверхні другого порядку
Лекція 5-7. Системи лінійних рівнянь. Розв’язування системи лінійних рівнянь методом Гауса. Правило Крамера. Розв’язок системи лінійних рівнянь за допомогою оберненої матриці.
3.1. Системи лінійних рівнянь
Лінійними операціями над якими-небудь об'єктами називаються їх додавання і множення на число.
Лінійною
комбінацією змінних
називається результат застосування до
них лінійних операцій, тобто
![]() де
де
![]() числа,
числа,
![]() змінні.
змінні.
Лінійним рівнянням називається рівняння виду
![]() (3.1)
(3.1)
де
![]() і b –
числа,
і b –
числа,
![]() – невідомі.
– невідомі.
Таким чином, у лівій частині лінійного рівняння є лінійна комбінація невідомих, а в правій – число.
Лінійне рівняння називається однорідним, якщо b=0. У протилежному випадку рівняння називається неоднорідним.
Системою лінійних рівнянь (лінійною системою) називається система виду
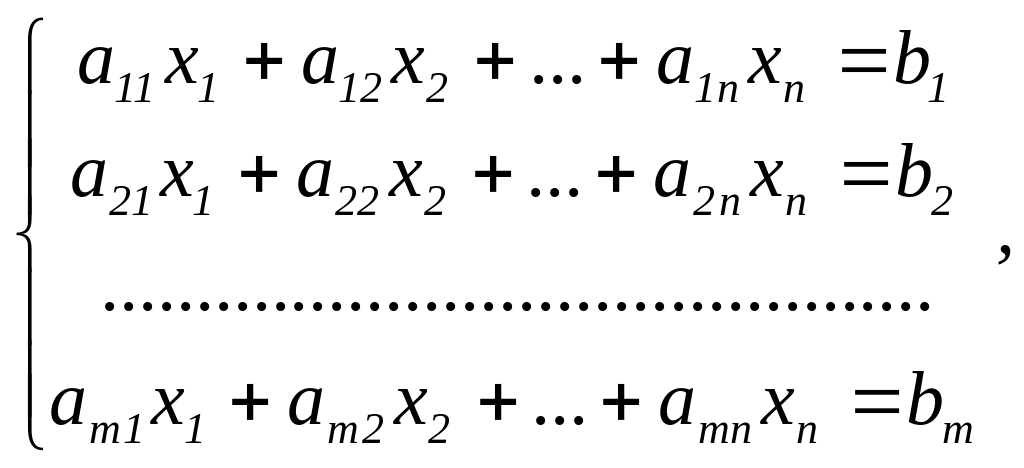 (3.2)
(3.2)
де
– коефіцієнти,
![]() – невідомі, n
– число невідомих, m
– число рівнянь,
– невідомі, n
– число невідомих, m
– число рівнянь,
![]() – вільні члени системи.
– вільні члени системи.
Розв’язком
лінійної системи (3.2) називається набір
чисел
![]() які при підстановці замість невідомих
перетворюють кожне рівняння системи у
правильну рівність.
які при підстановці замість невідомих
перетворюють кожне рівняння системи у
правильну рівність.
Система рівнянь називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку.
Теорема 3.1 (теорема Кронекера-Капеллі). Система (3.2) сумісна тоді і тільки тоді, якщо ранг матриці системи дорівнює рангу розширеної матриці.
Доведення.
Необхідність: нехай система (3.2) сумісна і
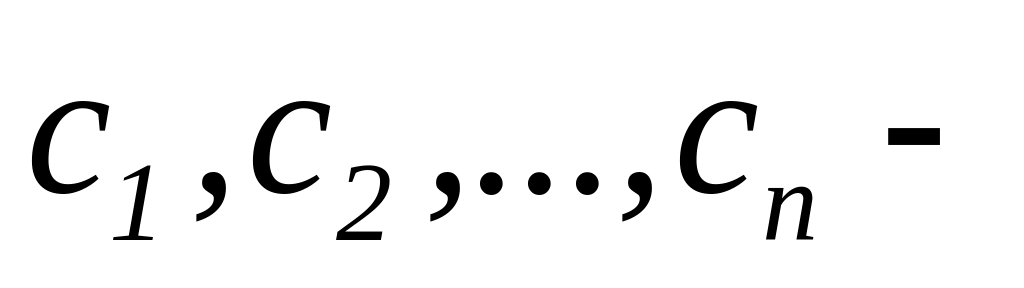 її
розв’язки. Тоді
її
розв’язки. Тоді
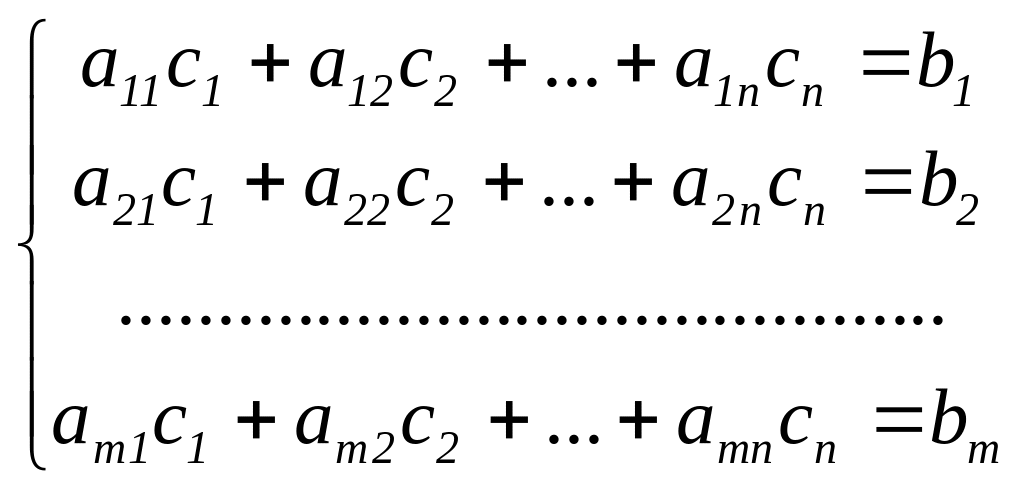 ,
тобто стовпець вільних членів є лінійною
комбінацією стовпців матриці системи
і, отже, стовпців будь-якого її базисного
мінору. Тому додавання елементів цього
стовпця і будь-якого рядка розширеної
матриці до базисного мінору дасть
нульовий визначник, тобто
,
тобто стовпець вільних членів є лінійною
комбінацією стовпців матриці системи
і, отже, стовпців будь-якого її базисного
мінору. Тому додавання елементів цього
стовпця і будь-якого рядка розширеної
матриці до базисного мінору дасть
нульовий визначник, тобто
![]()
2.
Достатність: якщо
![]() то
будь-який базисний мінор матриці А
є і базисним мінором розширеної матриці.
Тому стовпець вільних членів являє
собою лінійну комбінацію стовпців цього
базисного мінору, і, отже, лінійну
комбінацію всіх стовпців матриці А.
Якщо позначити коефіцієнти цієї лінійної
комбінації
то
будь-який базисний мінор матриці А
є і базисним мінором розширеної матриці.
Тому стовпець вільних членів являє
собою лінійну комбінацію стовпців цього
базисного мінору, і, отже, лінійну
комбінацію всіх стовпців матриці А.
Якщо позначити коефіцієнти цієї лінійної
комбінації
![]() то ці числа будуть розв’язком системи
(3.2), тобто ця система сумісна. Теорема
доведена.
то ці числа будуть розв’язком системи
(3.2), тобто ця система сумісна. Теорема
доведена.
Сумісна система називається визначеною, якщо вона має єдиний розв’язок, тобто існує тільки один набір п чисел який перетворює всі рівняння системи (3.2) в тотожності.
Сумісна система називається невизначеною, якщо вона має більше, ніж один розв’язок.
Дві системи лінійних рівнянь називаються еквівалентними, якщо вони мають одну й ту ж множину розв’язків.
3.2. Розв’язування систем лінійних рівнянь методом гаусса.
Лінійна система (3.2) може мати єдиний розв’язок, нескінченно багато розв’язків або не мати жодного розв’язку.
Приклади:
1.
![]() .
Єдиним розв’язком є пара чисел х=1,
у=2.
.
Єдиним розв’язком є пара чисел х=1,
у=2.
2.
![]() .
Розв’язком цієї системи будуть будь-які
два числа х
і у, які
задовольняють умові у=3–х.
Наприклад, х=1, у=2; х=0,
у=3 і т.д.
.
Розв’язком цієї системи будуть будь-які
два числа х
і у, які
задовольняють умові у=3–х.
Наприклад, х=1, у=2; х=0,
у=3 і т.д.
3.![]() . Очевидно, що ця система не має розв’язків,
тому що різниця двох чисел не може
приймати двох різних значень.
. Очевидно, що ця система не має розв’язків,
тому що різниця двох чисел не може
приймати двох різних значень.
Одним з найпоширеніших методів розв’язування системи лінійних рівнянь є метод послідовного виключення невідомих, або метод Гаусса
Умови існування і кількості розв’язків лінійної системи будуть вивчені надалі, а поки що розглянемо способи отримання єдиного розв’язку системи, у якій число рівнянь дорівнює числу невідомих:
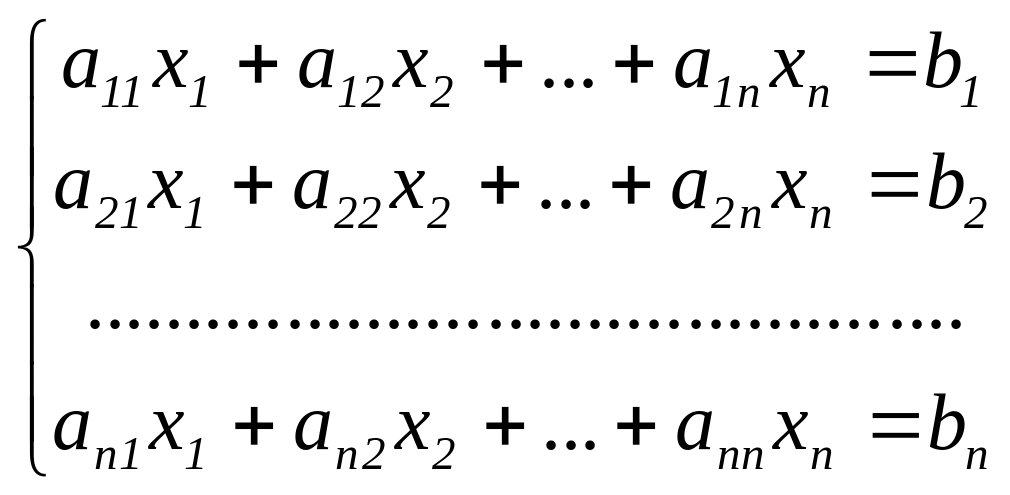 (3.3)
(3.3)
Нехай
![]() (цього завжди можна домогтися, помінявши
рівняння місцями). Розділимо обидві
частини першого рівняння на
(цього завжди можна домогтися, помінявши
рівняння місцями). Розділимо обидві
частини першого рівняння на
![]() і віднімемо отримане рівняння від
кожного з інших рівнянь системи,
помноживши його попередньо на
і віднімемо отримане рівняння від
кожного з інших рівнянь системи,
помноживши його попередньо на
![]() де i –
номер наступного рівняння. Як відомо,
отримана при цьому нова система буде
рівносильна вихідній. Коефіцієнти при
де i –
номер наступного рівняння. Як відомо,
отримана при цьому нова система буде
рівносильна вихідній. Коефіцієнти при
![]() у всіх рівняннях цієї системи, починаючи
з другого, будуть рівні 0,
тобто система виглядає так:
у всіх рівняннях цієї системи, починаючи
з другого, будуть рівні 0,
тобто система виглядає так:
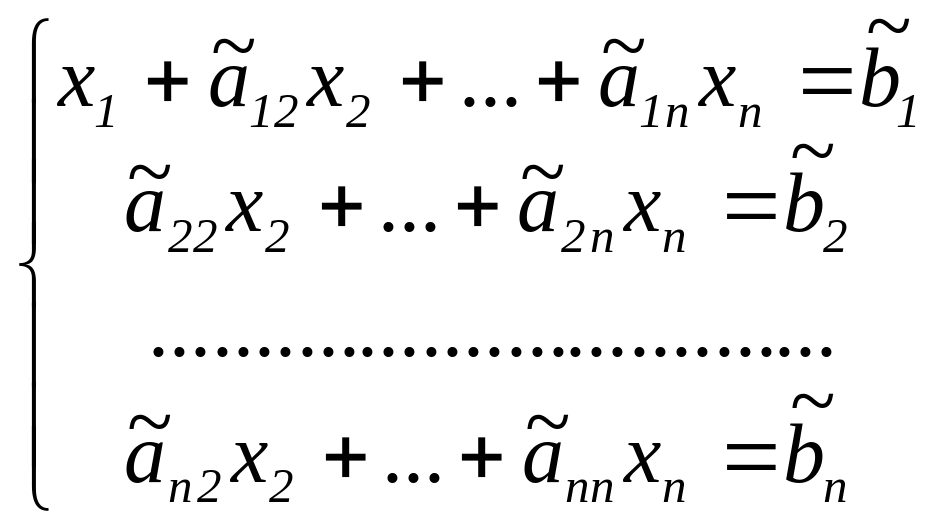 .
.
Таким
самим способом можна виключити
![]() з третього і наступного рівнянь.
Продовжуючи цю операцію для наступних
невідомих, приведемо систему до так
званого трикутного виду:
з третього і наступного рівнянь.
Продовжуючи цю операцію для наступних
невідомих, приведемо систему до так
званого трикутного виду:
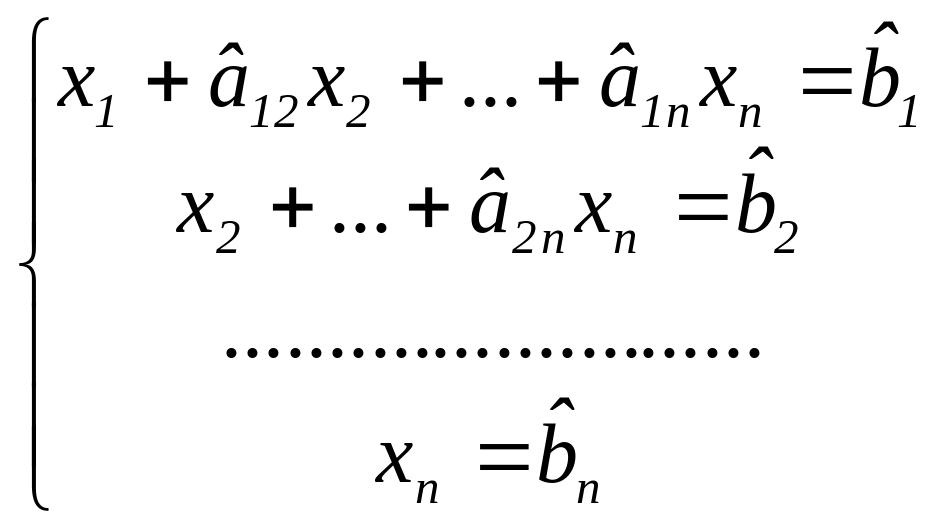 . (3.4)
. (3.4)
Тут
символами
![]() і
і
![]() позначені числові коефіцієнти, які
змінилися в результаті перетворень, і
вільні члени.
позначені числові коефіцієнти, які
змінилися в результаті перетворень, і
вільні члени.
З
останнього рівняння системи (3.4) єдиним
методом визначається
![]() ,
а потім послідовною підстановкою –
інші невідомі.
,
а потім послідовною підстановкою –
інші невідомі.
Зауваження. Іноді в результаті перетворень в якому-небудь з рівнянь перетворюються в 0 усі коефіцієнти і права частина, тобто вона перетворюється в тотожність 0=0. Виключивши її із системи, ми зменшимо число рівнянь у порівнянні з числом невідомих. Така система не може мати єдиного розв’язку.
Якщо ж у процесі застосування методу Гауса яке-небудь рівняння перетвориться в рівність виду 0=1 (коефіцієнти при невідомих перетворилися в 0, а права частина прийняла ненульове значення), то вихідна система не має розв’язку, тому що подібна рівність є невірною при будь-яких значеннях невідомих.
Приклади:
1.
Розв’яжемо методом Гауса систему
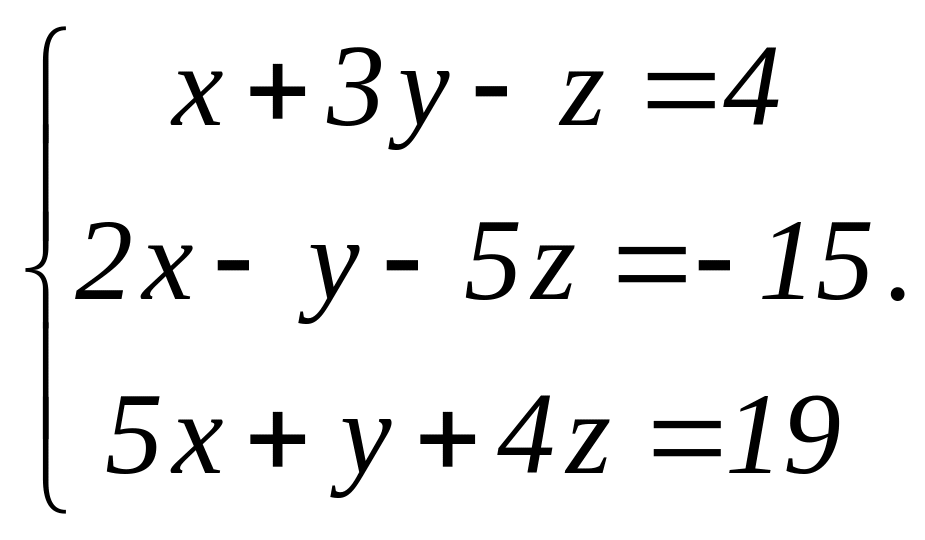
Віднімемо від другого рівняння подвоєне перше, а від третього – перше, помножене на 5.
Отримаємо:
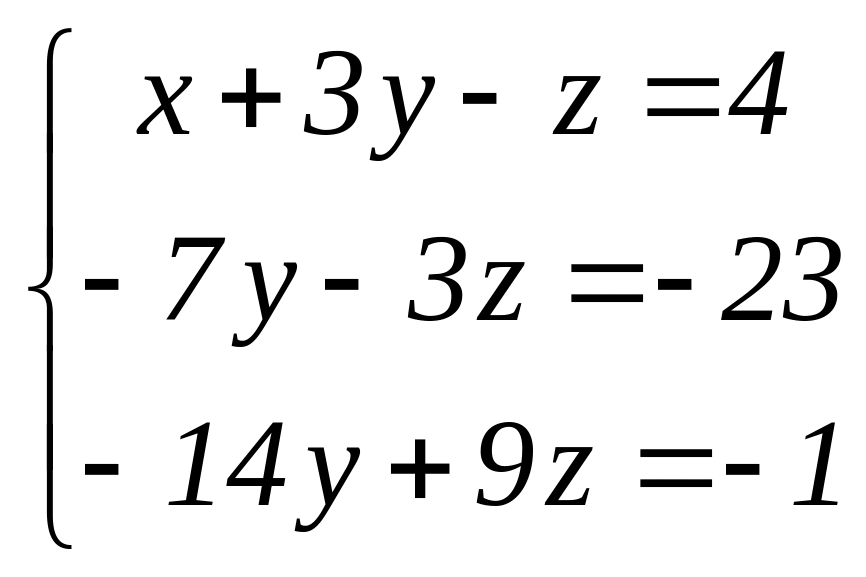 . Тепер віднімемо від третього рівняння
подвоєне друге, а потім розділимо друге
рівняння на –7
(коефіцієнт при у),
а третє – на 14
(новий коефіцієнт при z).
Система набуде вигляду:
. Тепер віднімемо від третього рівняння
подвоєне друге, а потім розділимо друге
рівняння на –7
(коефіцієнт при у),
а третє – на 14
(новий коефіцієнт при z).
Система набуде вигляду:
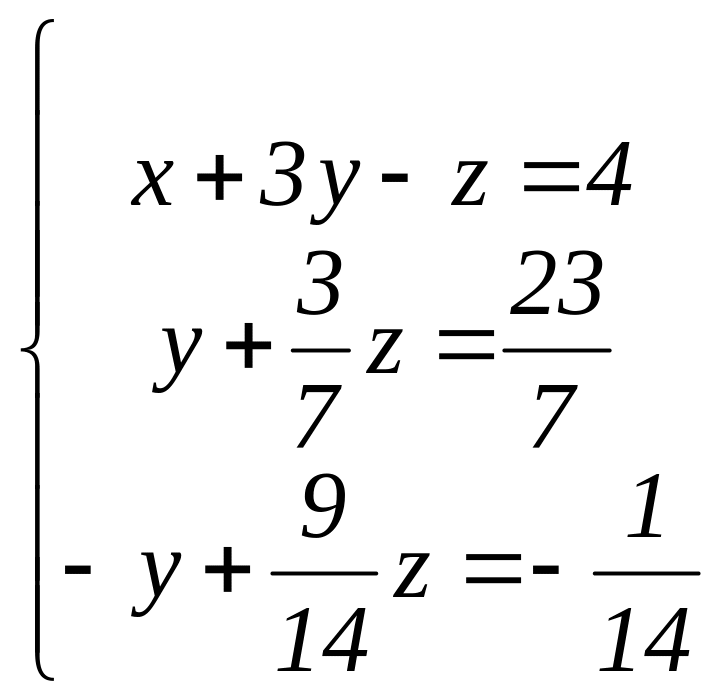 .
Тепер віднімемо від третього рівняння
помноженого на -1,
друге рівняння. Система набуде вигляду:
.
Тепер віднімемо від третього рівняння
помноженого на -1,
друге рівняння. Система набуде вигляду:
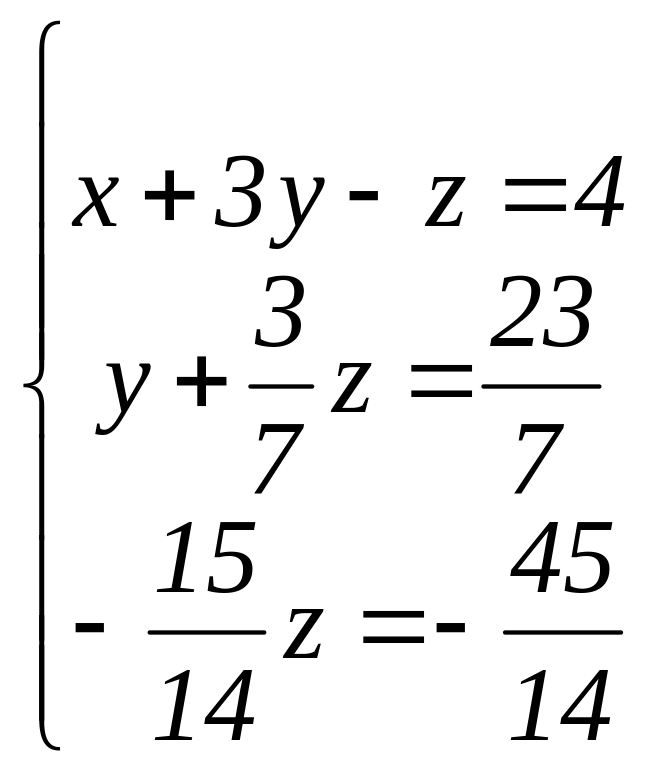 .
.
Звідси z=3, y=2, x=1 – єдиний розв’язок системи.
2.
Система
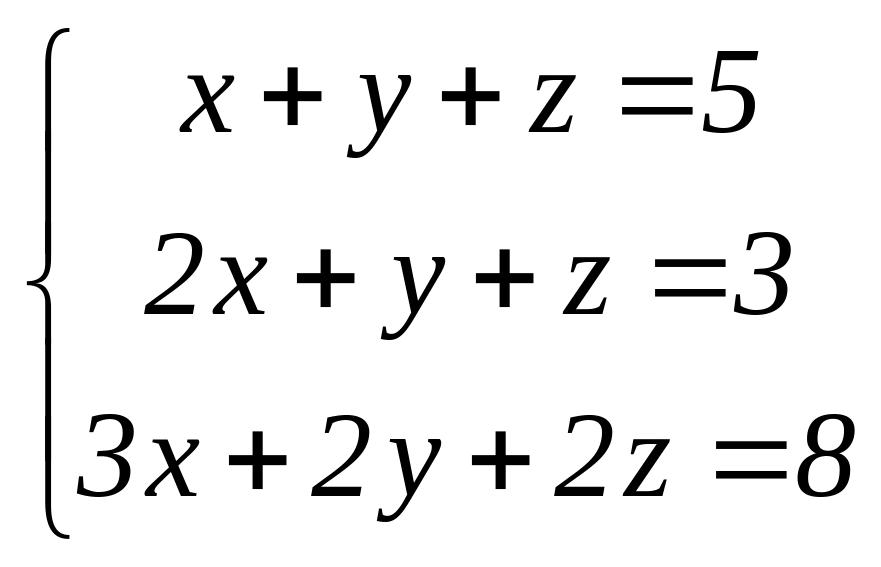 після виключення х
із другого і третього рівнянь набуде
вигляду:
після виключення х
із другого і третього рівнянь набуде
вигляду:
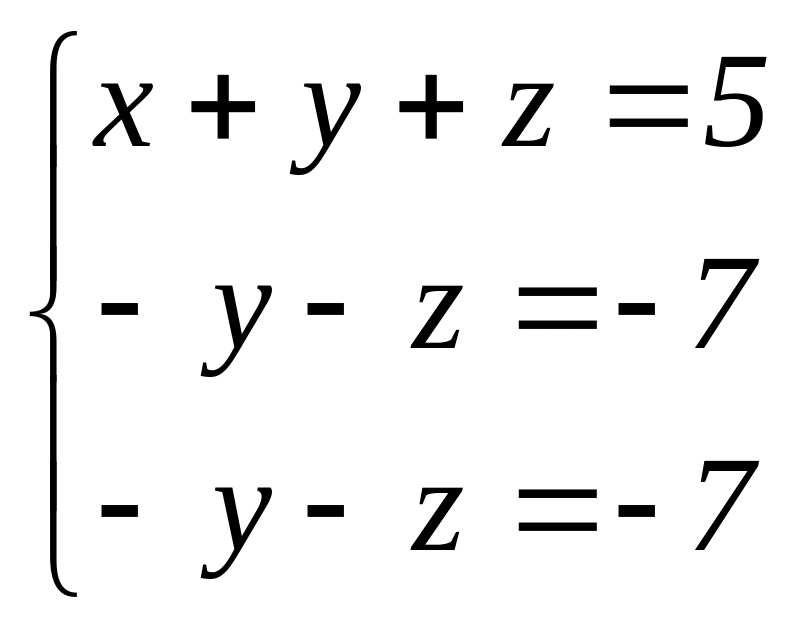 .
Якщо потім відняти друге рівняння від
третього, то останнє рівняння стане
тотожністю 0=0.
У системі залишилося два рівняння:
.
Якщо потім відняти друге рівняння від
третього, то останнє рівняння стане
тотожністю 0=0.
У системі залишилося два рівняння:
![]() .
Їх розв’язки можна записати у виді:
х=5, у
– будь-яке число, z=7–y.
Таким чином, система має нескінченно
багато розв’язків.
.
Їх розв’язки можна записати у виді:
х=5, у
– будь-яке число, z=7–y.
Таким чином, система має нескінченно
багато розв’язків.
3.
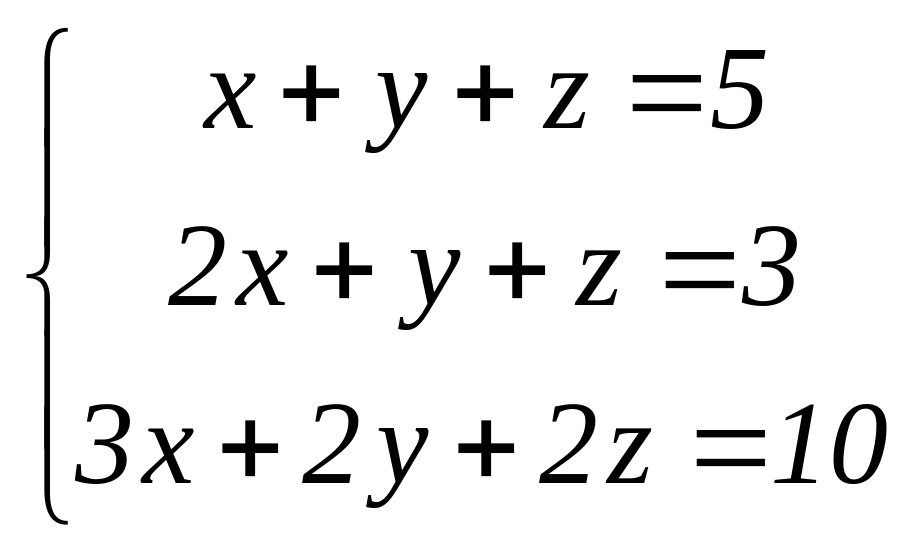 .
Застосувавши до цієї системи метод
Гаусса, одержимо
.
Застосувавши до цієї системи метод
Гаусса, одержимо
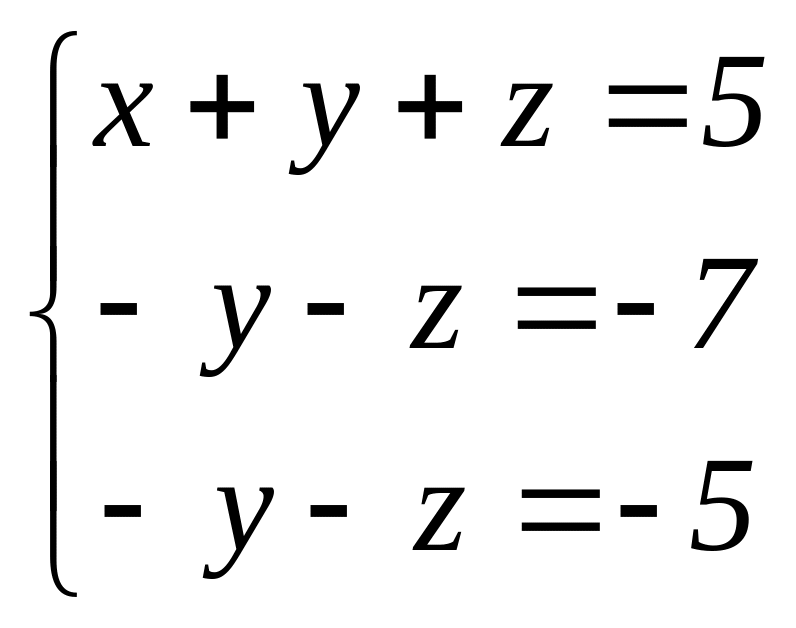 ,
звідки
,
звідки
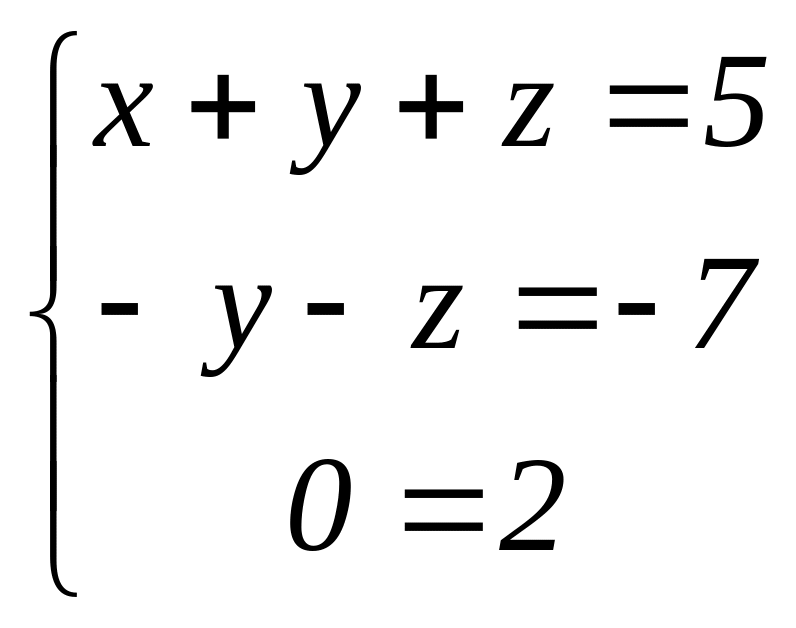 .
Остання рівність є невірною при будь-яких
значеннях невідомих, отже, система не
має розв’язку.
.
Остання рівність є невірною при будь-яких
значеннях невідомих, отже, система не
має розв’язку.
