2.2. Дії над матрицями

1. Додавання матриць.

Операція додавання матриць вводиться тільки для матриць однакового розміру.

Сумою матриць А і В однакової розмірності m n називається матриця С тієї ж розмірності, кожен елемент якої дорівнює сумі елементів матриць А і В, що розміщені на тих же місцях:

Властивості додавання:

• А+В=В+А.

• (А+В)+С=А+(В+С).

• Якщо О – нульова матриця, то А+О=О+А=А.

Справедливість цих властивостей випливає з визначення операції додавання матриць.

Відзначимо ще раз, що додавати можна тільки матриці однакової розмірності.

Приклад.

2. Множення матриці на число.

Добутком матриці на число називається матриця тієї ж розмірності, що і вихідна, всі елементи якої дорівнюють елементам вихідної матриці, помноженим на дане число.

Властивості множення матриці на число:

• (km)A=k(mA).

• k(A+B)=kA+kB.

• (k+m)A=kA+mA.

Приклад.

. Тоді

3. Різниця матриць А-В визначається як сума матриці А і матриці В, помноженої на -1, тобто А-В=А+(-1)В.

Перемножування матриць

Вище було зазначено, що додавання матриць накладає умови на розмірності доданків. Множення матриці на матрицю теж вимагає виконання визначених умов для розмірностей співмножників, а саме: число стовпців першого множника повинно дорівнювати числу рядків другого.

Добутком матриці А розмірності m p і матриці В розмірності називається матриця С розмірності , кожен елемент якої визначається формулою: Таким чином, елемент являє собою суму добутків елементів i-го рядка матриці А на відповідні елементи j-го стовпця матриці В.

Приклад.

. При цьому існує добуток АВ, але не існує добутку ВА. Розмірність матриці С=АВ складає Знайдемо елементи матриці С:

Отже,

Теорема 2.1 (без доведення). Визначник добутку двох квадратних матриць дорівнює добутку їхніх визначників.

Зауважимо. Операція перемножування матриць не комутативна, тобто Дійсно, якщо існує добуток АВ, то ВА може взагалі не існувати через розбіжність розмірностей (див. попередній приклад). Якщо існують і АВ, і ВА, то вони можуть мати різні розмірності (якщо ).

Для квадратних матриць одного порядку добутки АВ і ВА існують і мають однакову розмірність, але їх відповідні елементи в загальному випадку не рівні.

Однак у деяких випадках добутки АВ і ВА збігаються.

Розглянемо добуток квадратної матриці А на одиничну матрицю Е того ж порядку:

Такий самий результат одержимо і для добутку ЕА. Отже, для будь-якої квадратної матриці А: АЕ=ЕА=А.

2.3. Обернена матриця

Нехай А – квадратна матриця. Матриця А^-1 називається оберненою до матриці А, якщо виконується умова

АА^-1= А^-1А=Е.

Квадратна матриця А називається виродженою, якщо , і невиродженою, якщо .

Розглянемо умову існування матриці, оберненої до даної, і спосіб її обчислення.

Теорема 2.2. Для існування оберненої матриці необхідно і достатньо, щоб матриця А була невиродженою.

Доведення.

1. Необхідність: нехай обернена матриця А^-1 існує, тоді Застосувавши правило знаходження добутку двох матриць, отримаємо 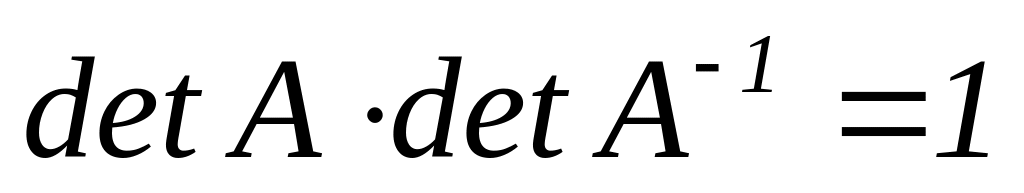(теорема 2.1), тому

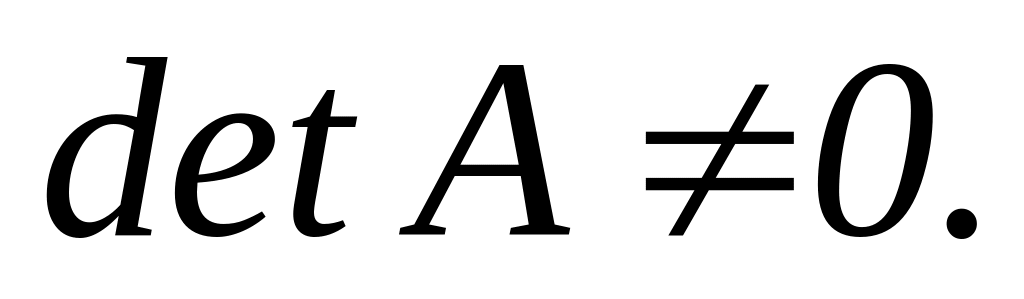
2. Достатність: нехай , тоді матриця А має обернену матрицю А^-1, причому

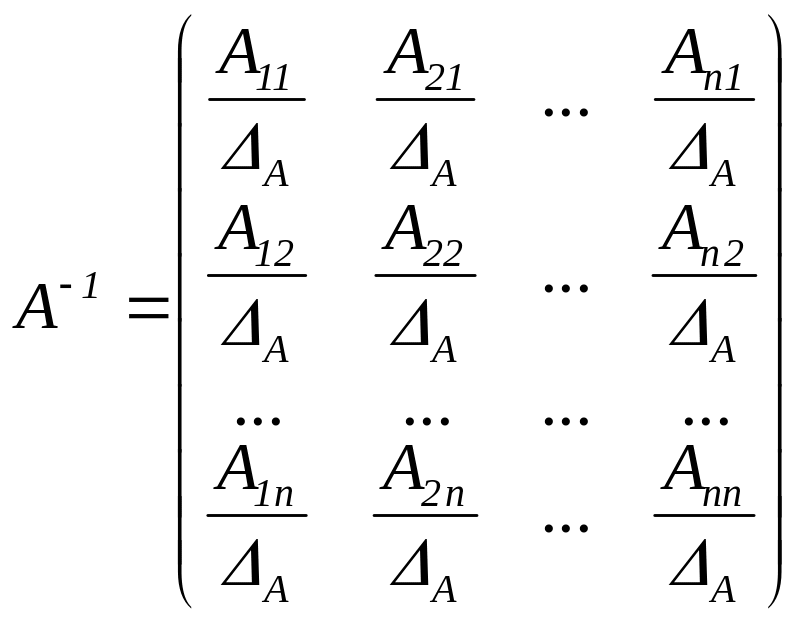, (2.1)

де – алгебраїчні доповнення елементів визначника матриці

. (2.2)

Тоді будь-який елемент добутку (або ) матриць (2.1) і (2.2) дорівнюють матриці, у якої всі елементи головної діагоналі дорівнюють одиниці (за теоремою 1.1), а всі діагональні елементи – нулю (за теоремою 1.2). Отже = =Е. Теорема доведена.

Покажемо, що – єдина обернена матриця. Нехай – ще одна обернена матриця, тоді

= Е= (А )=( А) =Е = .

Зауваження. Сформулюємо ще раз спосіб обчислення оберненої матриці: її елементами є алгебраїчні доповнення до елементів транспонованої матриці А, поділені на її визначник.

Приклад.

Знайдемо матрицю, обернену до

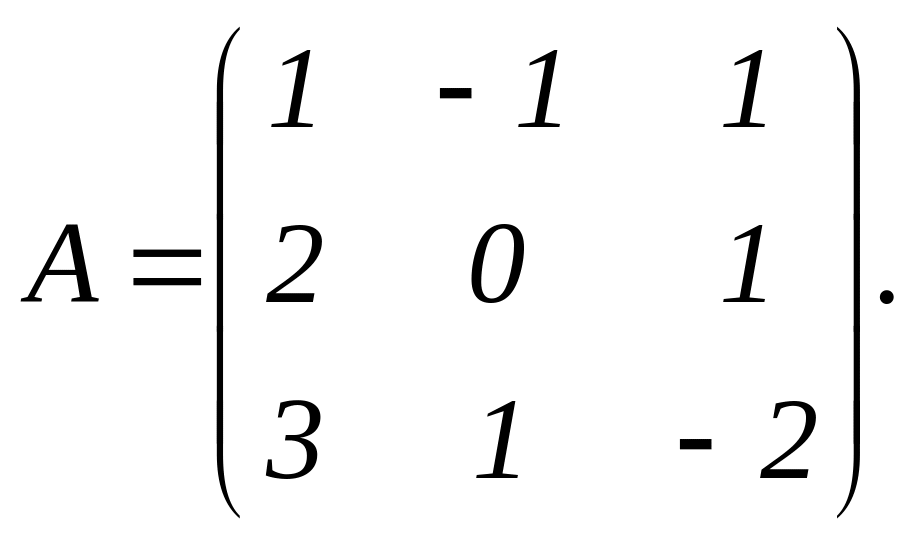
отже, матриця А невироджена. Знайдемо алгебраїчні доповнення до її елементів:

Не забудемо, що алгебраїчні доповнення до елементів рядка матриці А утворюють у зворотній матриці стовпець з тим же номером. Отже, Можна переконатися, що знайдена матриця дійсно задовольняє визначенню Знайдемо

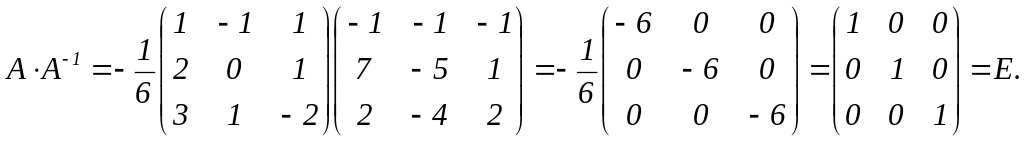
Той же результат отримаємо і при перемножуванні в зворотному порядку.