
- •Лекція 1-2. Визначники. Визначники другого і третього порядків та їх властивості. Розклад визначника за елементами рядка або стовпця. Поняття про визначники вищих порядків.
- •Визначники. Визначники другого і третього та їх властивості
- •1.2. Розклад визначника за елементами рядка або стовпця
- •1.3. Поняття про визначники вищих порядків
- •Лекція 3-4. Визначення матриці. Дії над матрицями. Обернена матриця. Ранг матриці. Теорема про ранг.
- •2.1. Визначення матриці
- •2.2. Дії над матрицями
- •Властивості додавання:
- •Властивості множення матриці на число:
- •Перемножування матриць
- •2.3. Обернена матриця
- •2.4. Ранг матриці, теорема про ранг.
- •Лекція 5-7. Системи лінійних рівнянь. Розв’язування системи лінійних рівнянь методом Гауса. Правило Крамера. Розв’язок системи лінійних рівнянь за допомогою оберненої матриці.
- •3.1. Системи лінійних рівнянь
- •3.2. Розв’язування систем лінійних рівнянь методом гаусса.
- •3.3. Правило крамера.
- •3.4. Розв’язок системи лінійних рівнянь за допомогою оберненої матриці.
- •Лекція 9-10. Поняття вектора. Лінійні операції над векторами. Скалярний добуток двох векторів. Векторний і мішаний добуток двох векторів.
- •4.1. Поняття вектрора
- •4.2. Лінійні операції над векторами
- •Додавання векторів.
- •Різниця векторів.
- •Множення вектора на число.
- •4.3. Скалярний добуток двох векторів
- •4.4. Векторний і мішаний добуток двох векторів
- •11.1. Системи координат на площині і в просторі.
- •Декартові координати на прямій.
- •11.2. Декартові координати на площині
- •11.3. Декартові координати в просторі
- •11.4. Полярні координати на площині
- •11.5. Циліндричні координати в просторі
- •116. Сферичні координати в просторі
- •5.7. Перетворення декартових координат
- •Паралельне перенесення
- •Поворот навколо початку координат
- •Лекція 12. Пряма на площині. Пряма на площині. Різні види рівнянь прямої на площині. Кут між двома прямими. Відстань від точки до прямої.
- •12.2. Кут між двома прямими, відстань від точки до прямої
- •Лекція 13. Площина у просторі. Площина у просторі. Рівняння площини що проходить через три точки. Кут між двома площинами.. Відстань від точки до площини
- •13.1. Рівняння площини
- •13.2. Кут між площинами, відстань від точки до площини
- •Лекція 14. Пряма у просторі. Пряма у просторі. Кут між двома прямими. Кут між прямою і площиною
- •14.3. Рівняння прямої у просторі
- •14.2. Взаємне розміщення прямої і площини у просторі
- •Лекція 15. Лінії другого порядку.
- •15.1. Криві другого порядку
- •Лекція 16. Лінії другого порядку.
- •16.1. Поверхні другого порядку
13.2. Кут між площинами, відстань від точки до площини
Розглянемо дві площини і , які задано відповідно рівняннями
![]() ,
,
![]() .
.
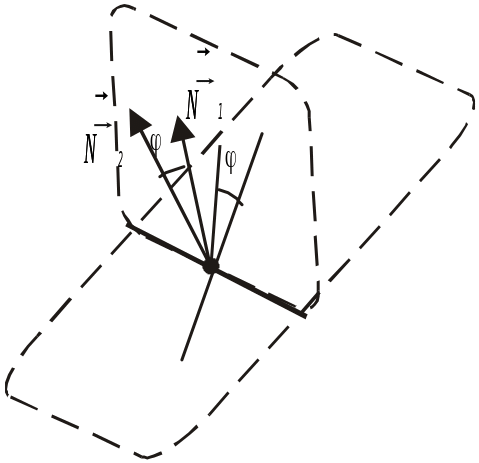
Рис. 2.21
Двогранний
кут
між площинами
і
дорівнюватиме куту між векторами
![]() і
і
![]() ,
перпендикулярними до цих площин (рис.
2.21), тому
,
перпендикулярними до цих площин (рис.
2.21), тому
![]() . (2.28)
. (2.28)
Якщо
площини взаємно перпендикулярні, то
![]() і, розкривши скалярний добуток у формулі
(2.28), дістанемо умову перпендикулярності
двох площин:
і, розкривши скалярний добуток у формулі
(2.28), дістанемо умову перпендикулярності
двох площин:
![]() . (2.29)
. (2.29)
Якщо
площини
і
паралельні між собою, то їхні вектори
![]() і
— колінеарні,
а отже, відповідні координати пропорційні,
і ми маємо умову
паралельності двох площин
і
— колінеарні,
а отже, відповідні координати пропорційні,
і ми маємо умову
паралельності двох площин
![]() . (2.30)
. (2.30)
За
аналогією з формулою знаходження
відстані від точки до прямої на площині
можна записати формулу знаходження
відстані від точки
![]() до площини
до площини
![]() .
Вона набирає вигляду
.
Вона набирає вигляду
![]() .
.
Лекція 14. Пряма у просторі. Пряма у просторі. Кут між двома прямими. Кут між прямою і площиною
14.3. Рівняння прямої у просторі
Пряму у просторі можна задати як лінію перетину двох площин у прямокутній системі координат:
![]() (2.31)
(2.31)
Зрозуміло,
що ці площини мають бути непаралельними,
тобто їхні нормальні вектори
![]() ,
— не колінеарні. Система (2.31) називається
загальним
рівнянням прямої.
Дістанемо ще деякі форми рівняння
прямої.
,
— не колінеарні. Система (2.31) називається
загальним
рівнянням прямої.
Дістанемо ще деякі форми рівняння
прямої.
Канонічне
рівняння прямої.
Нехай у системі координат Охуz
задано пряму l
і ненульовий вектор
![]() ,
колінеарний цій прямій. Точка
,
колінеарний цій прямій. Точка
![]() належить прямій, а напрямний вектор
належить прямій, а напрямний вектор
![]() .
Тоді довільна точка М
(х,
у,
z)
лежатиме на прямій тоді і тільки тоді,
коли вектори
.
Тоді довільна точка М
(х,
у,
z)
лежатиме на прямій тоді і тільки тоді,
коли вектори
![]() і
колінеарні:
і
колінеарні:
![]() .
(2.32)
.
(2.32)
Рівняння (2.32) називається канонічним рівнянням прямої у просторі.
Параметричне рівняння.
У рівнянні прямої (2.32) позначимо через t кожне з рівних відношень. Тоді
![]() .
.
Звідси дістаємо:

Параметричне рівняння прямої в просторі.
Рівняння прямої, що проходить через дві задані точки.
Нехай
дві точки
![]() і
і
![]() належать прямій у просторі. Тоді вектор
належать прямій у просторі. Тоді вектор
![]() можна розглядати як напрямний вектор
прямої. Замінюючи ним вектор
у рівнянні (2.32), дістанемо шукане рівняння
прямої у просторі
можна розглядати як напрямний вектор
прямої. Замінюючи ним вектор
у рівнянні (2.32), дістанемо шукане рівняння
прямої у просторі
![]() .
.
Маючи
кілька рівнянь однієї й тієї ж прямої,
поміркуємо, як дістати зв’язок між
ними. Розглянемо, як із загального
рівняння (2.31)
вивести канонічне рівняння (2.32). Для
цього потрібно знайти точку, яка лежить
на прямій, тобто розв’язати систему
(2.31), і напрямний вектор
прямої. Пригадуючи геометричний зміст
коефіцієнтів у рівнянні площини,
записуємо вектор
![]() — перпендикулярний
до першої площини, а
— перпендикулярний
до першої площини, а
![]() — неперпендикулярний
до другої.
— неперпендикулярний
до другої.
Рис. 2.22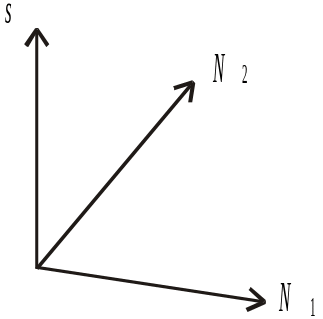
![]() .
Використовуючи запис век-
торного
добутку через визначник, дістаємо:
.
Використовуючи запис век-
торного
добутку через визначник, дістаємо:
![]() (2.33)
(2.33)
Для знаходження кута між двома прямими
![]() і
і
![]()
візьмемо
до уваги, що вектори
![]() і
і
![]() колінеарні відповідним прямим і
скористаємося формулою:
колінеарні відповідним прямим і
скористаємося формулою:
![]() .
.
З останньої формули випливає умова перпендикулярності двох прямих
![]() ,
,
а
умову паралельності двох прямих дістанемо
як умову колінеарності напрямних
векторів
![]() і
і
![]() :
:
![]() .
.
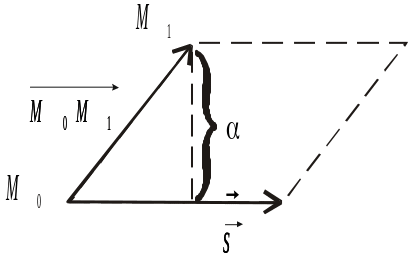
Рис. 2.23![]() до прямої
.
до прямої
.
Шукану
відстань можна розглянути як довжину
висоти паралелограма, побудованого на
векторах
![]() і
(рис. 2.23). Із підрозд.
2.1.3 відомо, що
площа паралело-
грама дорівнює модулю
векторного добутку векторів, на яких
побудовано цей паралелограм. Доходимо
висновку, що шукану висоту, а отже, і
відстань від точки до прямої можна
знайти за формулою:
і
(рис. 2.23). Із підрозд.
2.1.3 відомо, що
площа паралело-
грама дорівнює модулю
векторного добутку векторів, на яких
побудовано цей паралелограм. Доходимо
висновку, що шукану висоту, а отже, і
відстань від точки до прямої можна
знайти за формулою:
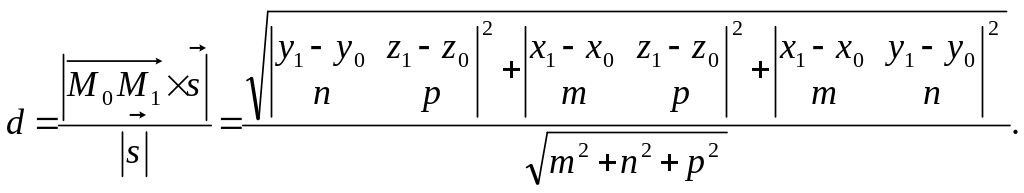 (2.34)
(2.34)
