Лекція 1-2. Визначники. Визначники другого і третього порядків та їх властивості. Розклад визначника за елементами рядка або стовпця. Поняття про визначники вищих порядків.

1. Визначники. Визначники другого і третього та їх властивості

Вираз

(1.1)

називається визначником (детермінантом) другого порядку. Поняття „визначник” (від латинського determino – визначаю) ввів В. Лейбніц.

Для обчислення визначника другого порядку потрібно від добутку елементів, що стоять на головній діагоналі, відняти добуток елементів, розміщених на побічній діагоналі.

Приклади.

1.

2.

Вираз

(1.2)

називається визначником (детермінантом) третього порядку.

Для того, щоб легше запам'ятати формулу для обчислення визначника третього порядку, можна використовувати так називане правило трикутників. Воно полягає в наступному: елементи, добутки яких входять у визначник зі знаком „+”, розташовуються так:

утворити два трикутники, симетричних щодо головної діагоналі. Елементи, добутки яких входять у визначник зі знаком „–” розташовуються аналогічним чином відносно побічної діагоналі:

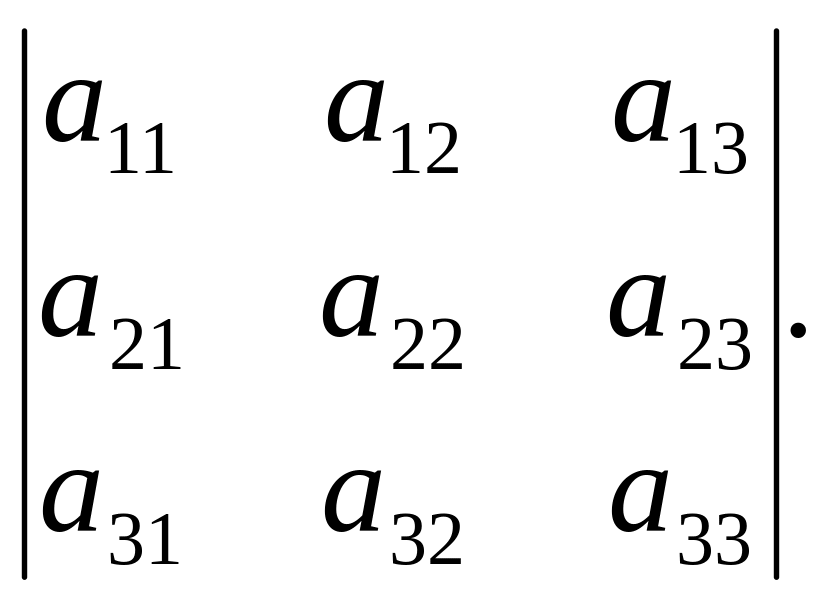
П риклади.

1.

2.

Символи називаються елементами визначника, причому перший індекс і показує номер рядка, а другий індекс j – номер стовпця, на перетині яких стоїть даний елемент. Так, елемент а₂₃ стоїть у другому рядку і третьому стовпці.

Елементи а₁₁ і а₂₂ у визначнику (1.1) і а₁₁, а₂₂, а₃₃ у визначнику (1.2) складають головну діагональ визначника, а елементи а₁₂, а₂₁ і а₁₃, а₂₂, а₃₁ в тих самих визначниках – побічну діагональ.

Зауважимо, що елементами визначника можуть бути не тільки числа, а й алгебраїчні чи тригонометричні вирази, функції тощо.

На прикладі визначників третього порядку розглянемо основні властивості визначників.

Властивість 1. Визначник не зміниться, якщо його рядки замінити відповідними стовпцями:

Доведення.

=

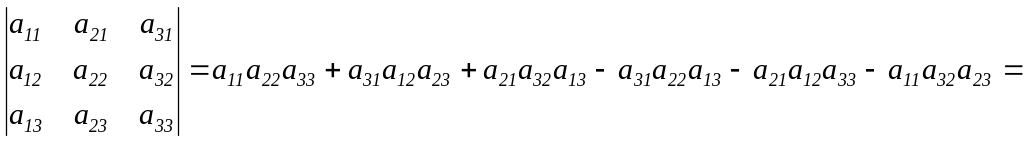
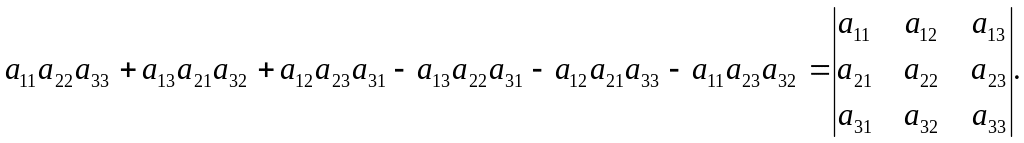
Властивість 2. Якщо переставити місцями два рядки (стовпці), то визначник поміняє знак.

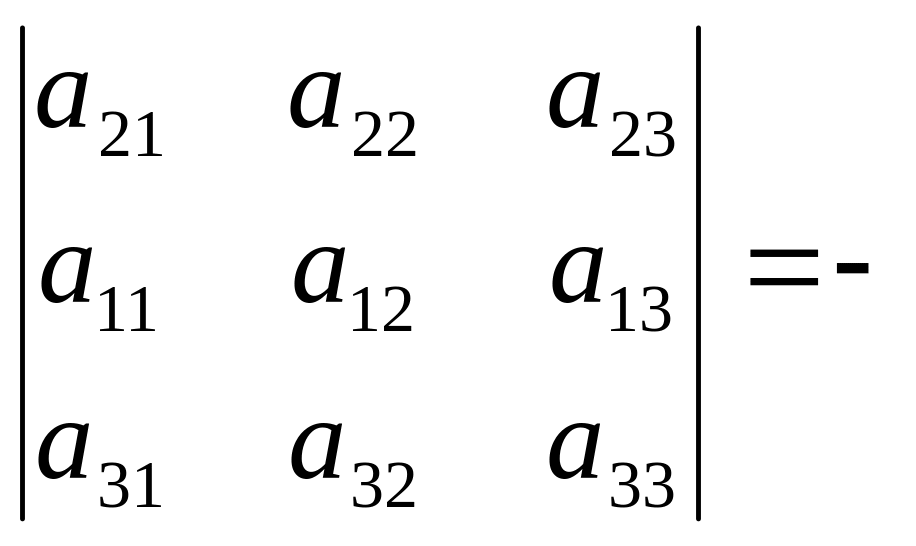
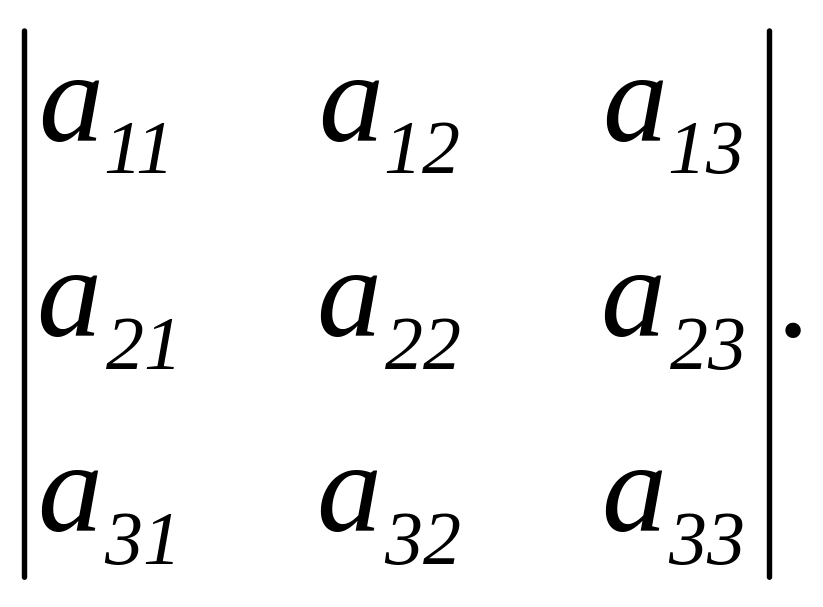
Доведення.

-

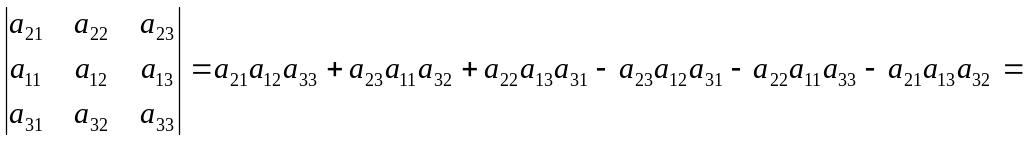
Властивість 3. Якщо один з рядків (стовпців) визначника складається тільки з нулів, то визначник дорівнює нулю.

Властивість 4. Якщо визначник має два однакових рядки (стовпці), то він дорівнює нулю.

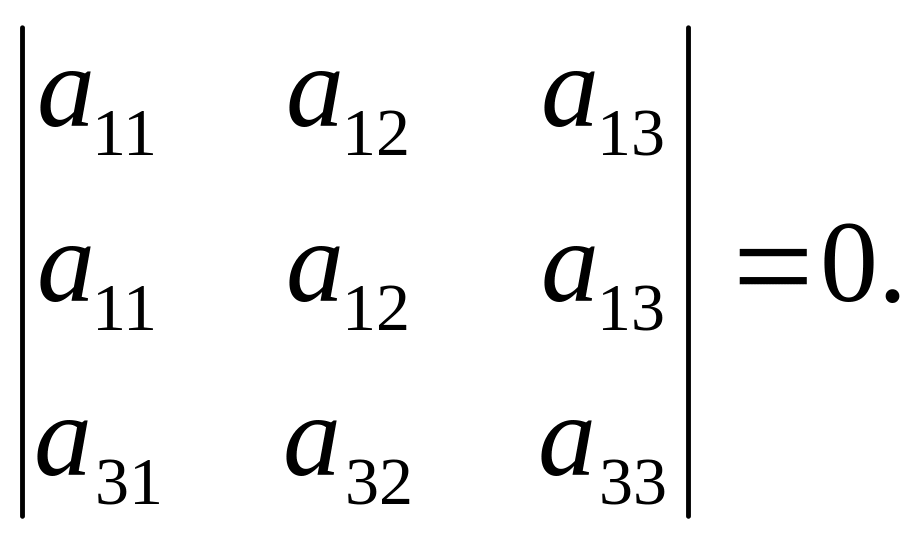
Доведення.

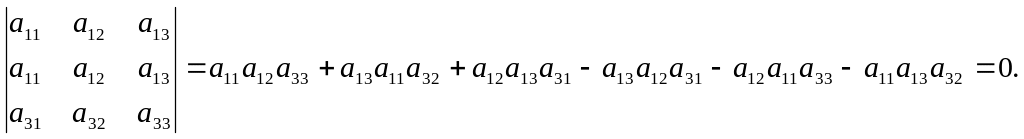
Властивість 5. Спільний множник, що міститься в усіх елементах одного рядка (стовпця), можна винести за знак визначника.

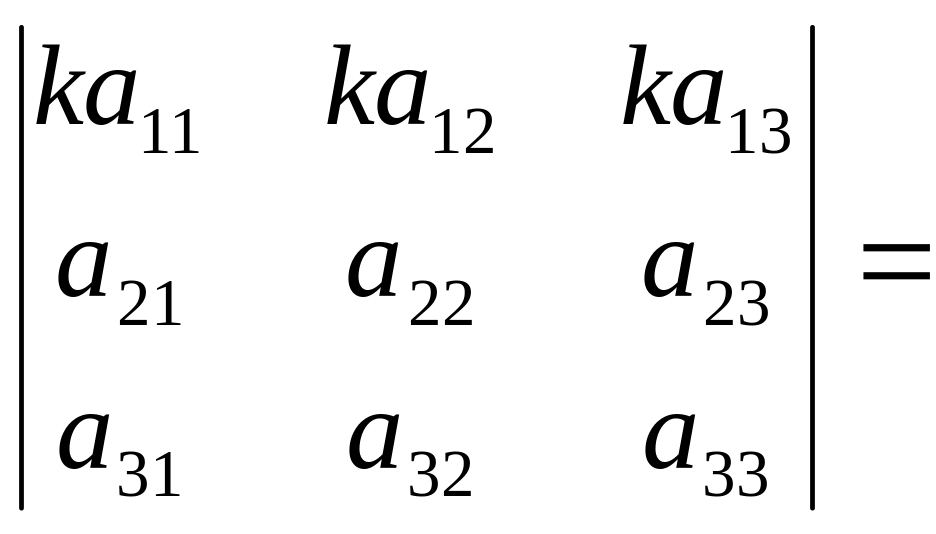
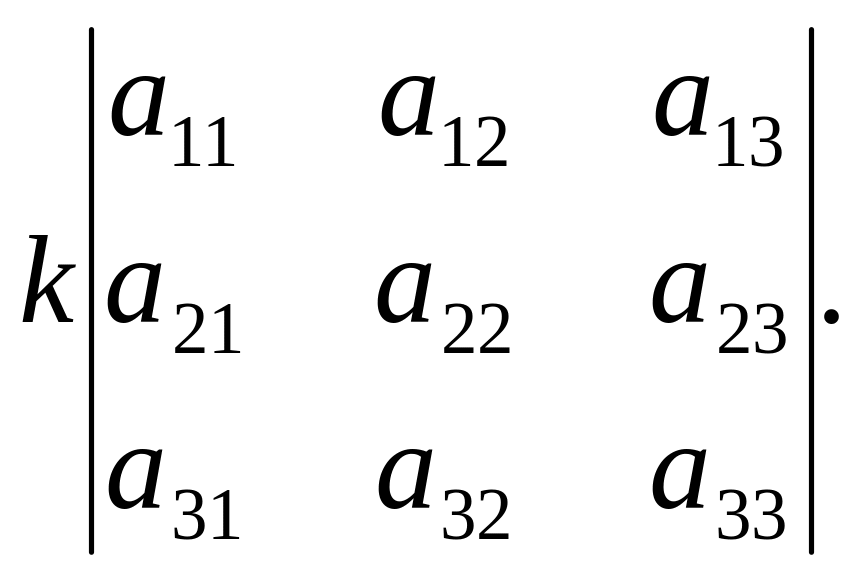
Доведення.

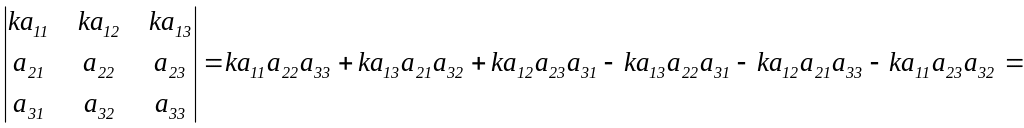
Властивість 6. Якщо у визначнику елементи двох рядків (стовпців) пропорційні, то визначник дорівнює нулю.

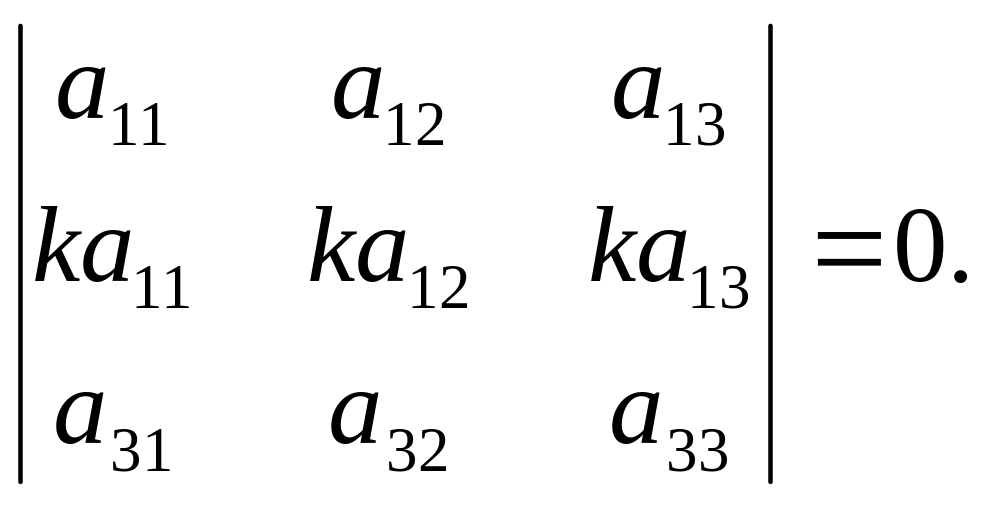
Властивість 7. Якщо кожен елемент п-го рядка (п-го стовпця) є сума двох доданків, то такий визначник дорівнює сумі двох визначників, у одного з яких п-й рядок (п-й стовпець) складається з двох доданків, а у другого з других; інші елементи усіх трьох визначників однакові.

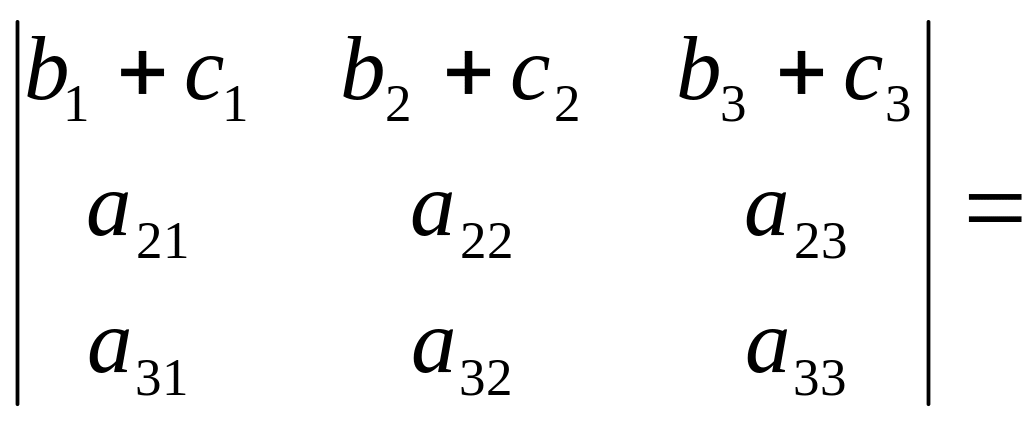
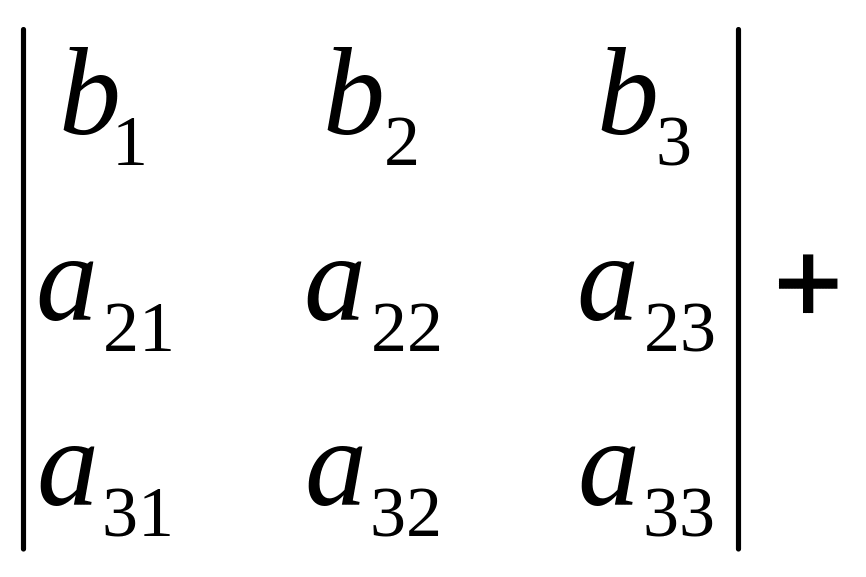
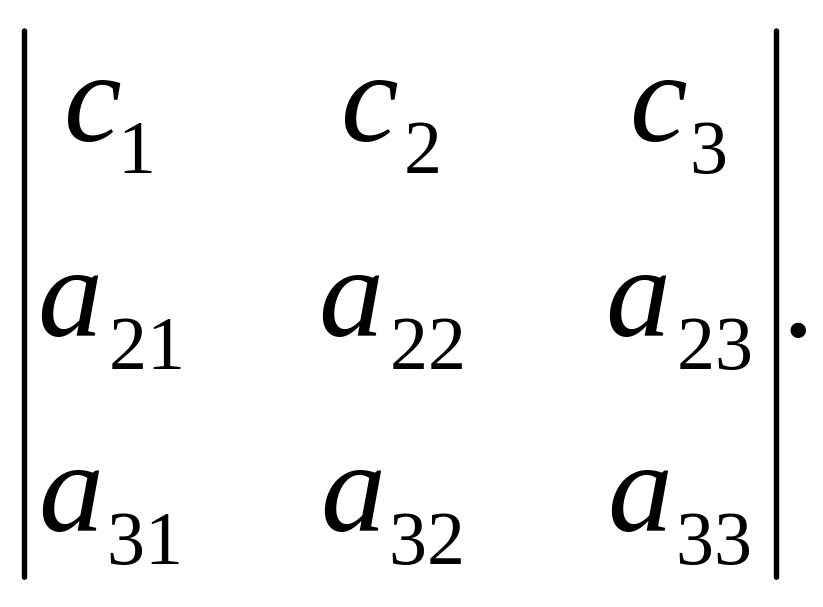
Властивість 8. Величина визначника не зміниться, якщо до елементів одного рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на одне й те саме число.

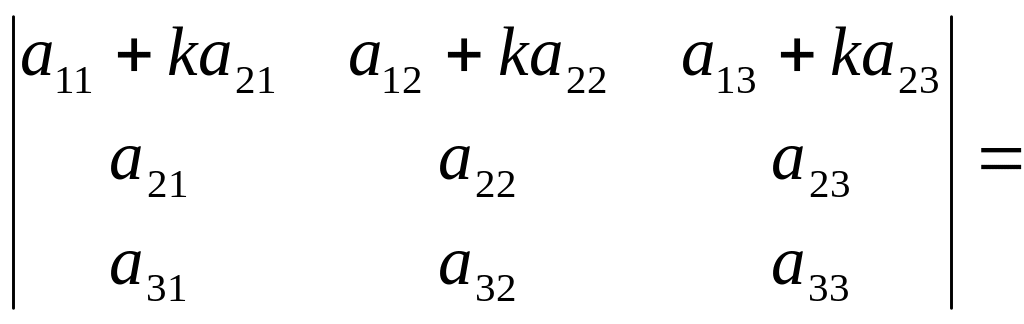
1.2. Розклад визначника за елементами рядка або стовпця

Нехай задано визначник третього порядку:

(1.3)

Мінором елемента визначника називається визначник, який отримується з даного визначника шляхом викреслювання рядка і-го рядка та j-го стовпця, у яких розміщений обраний елемент. Для визначника (1.3) мінорами елементів а₂₃ і а₃₂ є такі визначники:

.

Алгебраїчним доповненням елемента називається його мінор, взятий зі знаком , тобто

(1.4)

Тепер сформулюємо і наведемо приклад доведення теореми про розклад визначника за елементами рядка (стовпця).

Теорема 1.1. Визначник дорівнює сумі добутків елементів будь-якого його рядка або стовпця на їх алгебраїчні доповнення, тобто

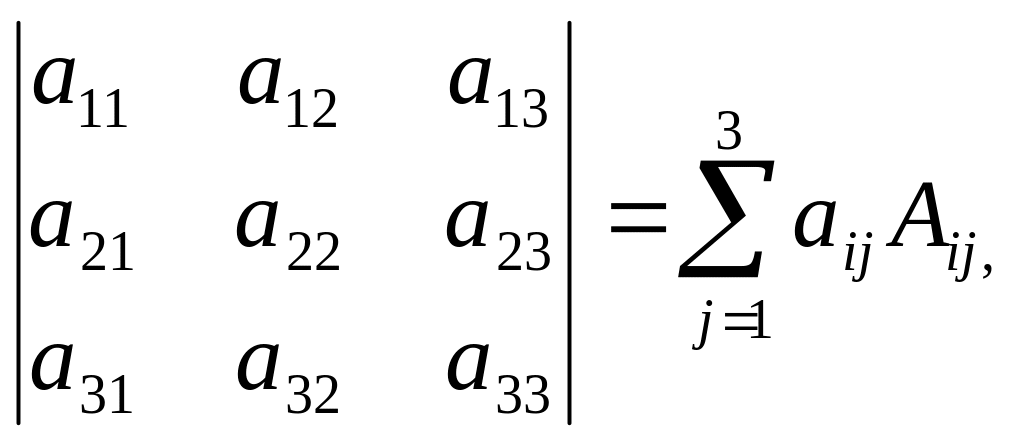де i=1,2,3.

Доведення.

Доведемо теорему для першого рядка визначника, тому що для будь-якого іншого рядка або стовпця можна провести аналогічні міркування і отримати той же результат.

Знайдемо алгебраїчні доповнення до елементів першого рядка:

Тоді

Таким чином, для обчислення визначника досить знайти алгебраїчні доповнення до елементів якого-небудь рядка або стовпця і обчислити суму їхніх добутків на відповідні елементи визначника.

Приклад. Обчислимо визначник 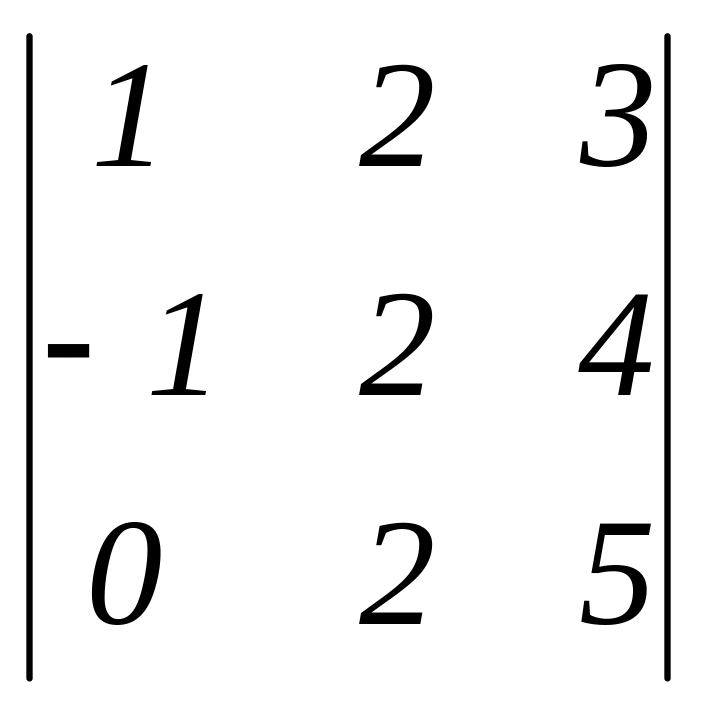за допомогою розкладання по першому стовпцю. Зауважимо, що при цьому шукати не потрібно, тому що отже, і Знайдемо і Отже,

=

Теорема 1.2. Сума добутків елементів будь-якого рядка або стовпця визначника на алгебраїчні доповнення відповідних елементів іншого рядка або стовпця дорівнює нулю.