5. Задача про максимальний потік.

Ця задача, як i задача про найкоротший шлях, є частинним випадком задачі про оптимальний потік. Із задачею про максимальний потік тісно пов'язана задача про мінімальний розріз мережі. Наведемо формулювання цих задач.

Розглянемо мережу, що визначається графом g, яка має єдине джерело s, єдиний стік t та означену на множині U функцію пропускної спроможності . Нехай інтенсивність джерела . За теоремою існування потоку на мережі інтенсивність стоку має бути рівною . Допустимий потік для розглядуваної мережі визначається співвідношеннями:

(1.8)

Задача про максимальний потік полягає у знаходженні максимального значення інтенсивності d, при якому в розглядуваній мережі існує потік. Потік , що відповідає максимальному значенню інтенсивності, називається максимальним потоком, а – величиною цього потоку.

Розглянемо описану вище мережу. Розрізом мережі, що відокремлює s від t, називається множина дуг , де C – деяка множина вершин ( ) мережі, така, що .

Нагадаємо, що пропускна спроможність цього розрізу визначається звичайним чином:

.

Зрозуміло, що для кожної конкретної мережі вибір множини C повністю визначає пропускну спроможність розрізу. Розріз, що має найменшу пропускну спроможність, називається мінімальним. Задача пошуку такого розрізу називається задачею про мінімальний розріз.

Виявляється, що сформульовані задачі є двоїстими i, як слід чекати, їх розв'язки тісно пов'язані між собою.

Теорема 1.3. (Форда-Фалкерсона). Величина максимального потоку із s в t дорівнює пропускній спроможності мінімального розрізу, що відокремлює s від t.

Наслідок. Якщо дуга (i,j) входить до мінімального розрізу, то величина максимального потоку по цій дузі дорівнює її пропускній спроможності . При цьому кажуть, що потік насичує дугу.

Для розв'язування задачі про максимальний потік Фордом та Фалкерсоном був розроблений метод, що носить їх ім'я.

6. Алгоритм методу Форда-Фалкерсона.

Згідно теореми про максимальний потік та мінімальний розріз за відомим максимальним потоком легко побудувати мінімальний розріз (див. співвідношення (1.9)). Крім того, якщо потік не є максимальним, то можливе його збільшення шляхом зміни потоку вздовж певного ланцюга. Ці факти лежать в основі методу Форда-Фалкерсона, що являє собою рекурентну процедуру, на кожному кроці якої позначаються вершини або будується потік більшої величини.

Алгоритм Форда-Фалкерсона розпочинає роботу з будь-якого допустимого потоку (зокрема нульового) величини . Згідно (1.9) для цього потоку визначається множина . Якщо , то потік є максимальним, в іншому випадку можна знайти та новий потік величини . Для нового потоку цей цикл операцій повторюється i т. д.

Процеси визначення та об'єднуються в один процес “розставлення позначок” вершин. Позначка (i) довільної вершини i складається з двох чисел та . Ці числа означають, що вздовж деякого ланцюга, останнім ребром якого є , можна додатково доставити одиниць потоку з вершини s до вершини i.

Дамо детальний виклад алгоритму, вважаючи, що відомий допустимий потік x (зокрема нульовий).

Алгоритм методу Форда-Фалкерсона.

Крок 1 (процес розставлення позначок). На цьому кроці кожна з вершин належить до одного з трьох типів:

– непозначена,

– позначена i непроглянута,

– позначена i проглянута.

Спочатку всі вершини непозначені.

Позначимо вершину s позначкою , що означає: можна послати потік з вершини s у саму себе необмеженої величини.

Тепер вершина s позначена i непроглянута.

Взагалі, нехай j – позначена i непроглянута вершина, або – її позначка. Розглядаємо ще непозначені вершини k: i . Кожній з таких вершин приписуємо позначку , де . Розглядаємо ще непозначені вершини k: i . Кожна з таких вершин одержує позначку , де .

Всі вершини k, які одержали позначки, тепер позначені i непроглянутi, а вершина j – позначена i проглянута.

Продовжуємо приписувати позначки непозначеним вершинам до тих пір, поки або вершина t виявиться позначеною, або не можна буде позначити жодної вершини i вершина t виявиться непозначеною.

У другому випадку існуючий потік x – максимальний, а множина позначених вершин визначає мінімальний розріз мережі.

У першому випадку існуючий потік x на кроці 2 можна збільшити.

Крок 2 (збільшення потоку). Нехай або – позначка вершини t. Це означає, що існуючий потік з s в t можна збільшити на величину . Для цього в першому випадку замінюємо на , у другому – замінюємо на .

Переходимо до вершини k i виконуємо аналогічні операції, змінюючи величину потоку на ту ж величину . Продовжуємо ці дії, поки не досягнемо вершини s. Після цього ліквідовуємо позначки всіх вершин i переходимо до кроку 1.

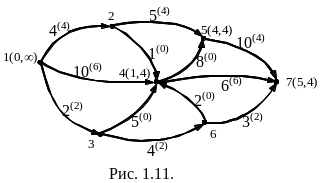
Приклад. Знайти максимальний потік з вершини 1 у вершину 7 на мережі, зображеній на рис. 1.8.

П роцес розв’язування задачі продовжено на рис. 1.9-11. Відповідь: , .