30. Моделі з паралельними сервісами

Розглянемо тепер моделі систем масового обслуговування з декількома паралельно працюючими засобами обслуговування (сервісами).

Модель (М/М/с): (GD//). Ця модель передбачає роботу с паралельних засобів обслуговува­ння. Інтенсивність вхідного потоку клієнтів дорівнює , а інтенсивність обслуговування клієнтів –  для кожного сервісу. Оскільки відсутні обмеження на кількість клієнтів у системі, то .

Результатом використання с паралельних сервісів є пропорційне збільшення інтенсивності обслуговування клієнтів системою до n, якщо , і до c якщо n>с. Отже, у термінах загальної моделі системи обслуговування і визначаються таким чином.

,

Отже,

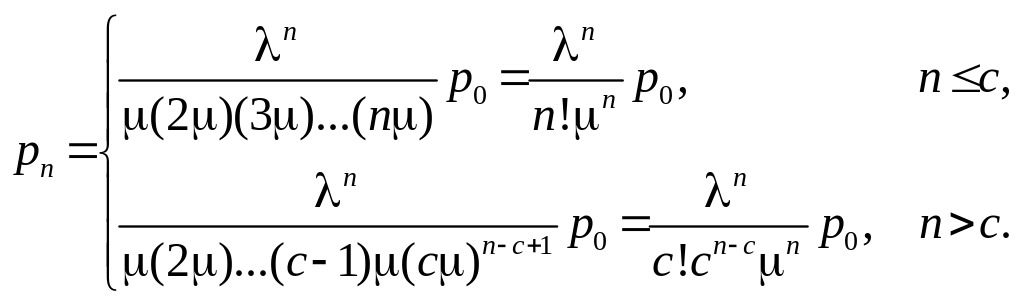
Значення імовірності визначається з рівняння . Позначивши і припускаючи, що , приходимо до наступної формули для :

.

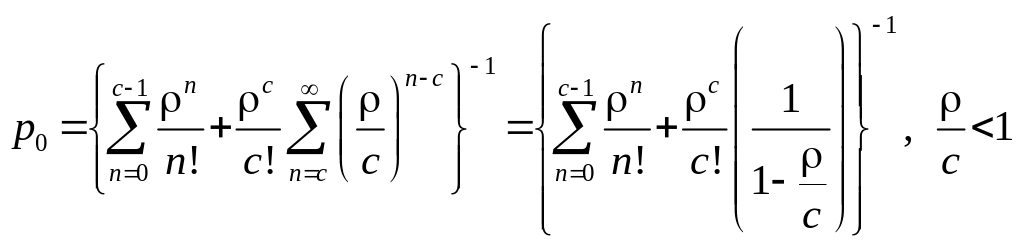Вираз для можна знайти так.

.

Оскільки , то ; значення для і можна знайти шляхом ділення на  значень і .

Модель (М/М/с): (GD/N/), с≤N. Ця модель обслуговуючої системи відрізняється від моделі (М/М/с):(GD//) тим, що ємність системи обмежена зверху значенням N (тоді максимальна довжина черги дорівнює N–с). Інтенсивності надходження і обслуговування клієнтів рівні  і  відповідно. Ефективна інтенсивність надходження заявок у систему обслуговування менше  у силу обмеженості ємності системи значенням N.

Параметри і загальної моделі обслуговуючої системи в даній моделі визначаються таким чином:

Підставляючи й у загальний вираз для і використовуючи позначення , одержуємо

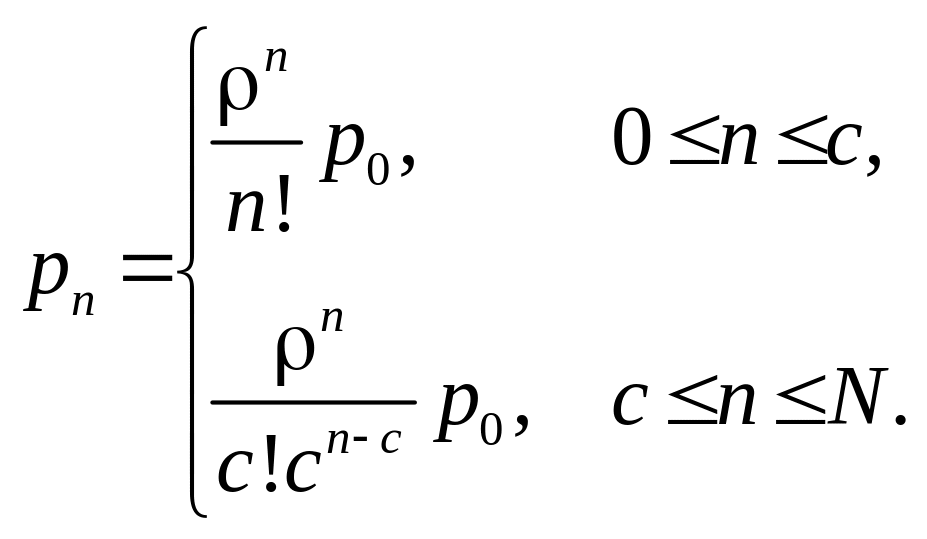
де

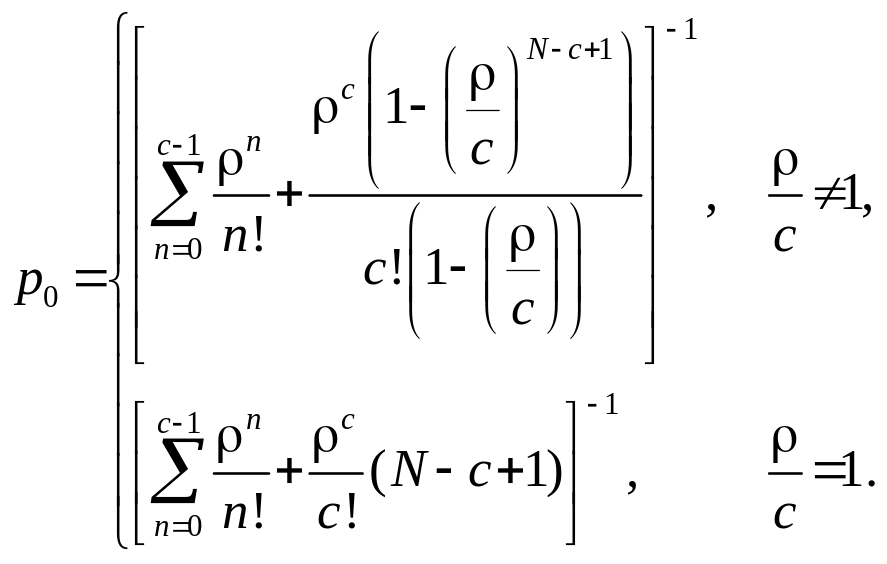
Далі обчислюємо для випадку, коли :

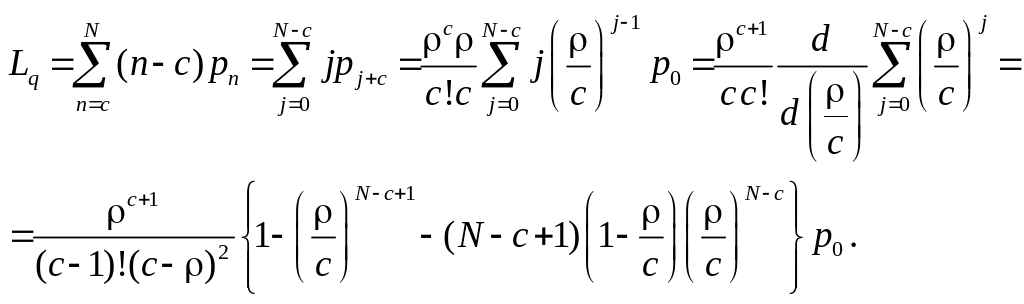
Можна також показати, що для випадку, коли , вираз для має такий вигляд:

.

Для визначення і, отже, і необхідно одержати вираз для . Оскільки жоден клієнт не може потрапити в систему після того, як досягнуто ліміт N за її місткістю, то

, .

Модель самообслуговування (М/М/): (GD//). У цій моделі кількість сервісів є необмеженою, оскільки клієнт виступає одночасно і у ролі сервісу. Передбачається, що інтенсивність надходження клієнтів  є постійною. Інтенсивність обслуговування  також є постійною. Скориставшись загальною моделлю, маємо

Отже,

З рівності випливає, що

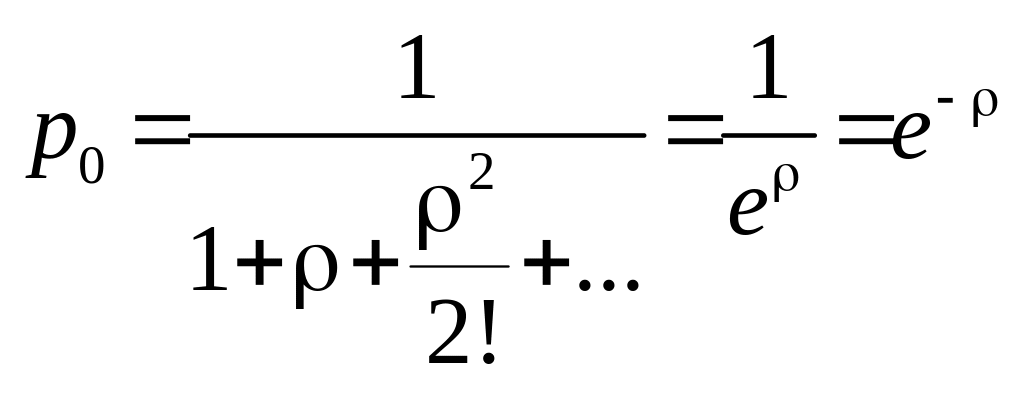. У результаті одержуємо

Ці імовірності збігаються з імовірностями розподілу Пуассона з математичним сподіванням . Як і слід було очікувати, тут (унаслідок принципу самообслуговування) .

56