24. Модель чистого народження

При заданій інтенсивності  надходжень клієнтів у систему обслуговування і досить малому інтервалі часу h>0 випливає, що

.

Тобто на досить малому часовому інтервалі h>0 може настати не більше однієї події (надходження клієнта). Отже, при h→0

.

Цей результат показує, що імовірність надходження клієнта протягом інтервалу h прямо пропорційна h з коефіцієнтом пропорційності, рівним інтенсивності надходжень .

Позначимо через імовірність надходження n клієнтів протягом часу t. Отже, при досить малому h>0 маємо наступне.

,

.

З першого рівняння випливає, що надходження n клієнтів протягом часу t+h можливе в двох випадках: якщо є n надходжень протягом часу t і немає надходжень за час h або є n–1 надходжень за час t і одне надходження за час h. Будь-які інші комбінації неможливі. Відповідно до умови незалежності стаціонарних приростів до правої частини рівняння застосуємо закон множення імовірностей. В другому рівнянні відсутність надходжень клієнтів протягом інтервалу t+h може мати місце лише у випадку, коли немає надходжень клієнтів за час h.

Перегруповуючи члени і переходячи до границі при h→0, одержуємо наступне.

,

,

де – похідна по t функції .

Розв’язок приведених вище різницево-диференціальних рівнянь має такий вигляд:

.

У даному випадку нами отримано дискретну щільність імовірності розподілу Пуассона з математичним сподіванням надходжень за час t. Дисперсія розподілу Пуассона також дорівнює t.

Отриманий результат означає, що усякий раз, коли часові інтервали між моментами послідовних надходжень заявок розподілені за експонентним законом з математичним сподіванням , число надходжень заявок в інтервалі, рівному t одиниць часу, характеризується розподілом Пуассона з математичним сподіванням t. Вірним є і зворотне твердження.

25. Модель чистої загибелі

У даній моделі передбачається, що система починає функціонувати, коли в момент часу 0 у ній є N клієнтів і не допускається жодного нового надходження клієнта. Клієнти після завершення їх обслуговування вибувають із системи з інтенсивністю  клієнтів в одиницю часу. Нехай – імовірність того, що після t часових одиниць у системі залишається n клієнтів. Для одержання різницево-диференціальних рівнянь відносно звичайно додержуються логіки міркувань, використаних у моделі чистого народження (розділ 7.4-1). Тому маємо

,

,

.

Ці рівняння мають розв’язки

,

які називаються усіченим розподілом Пуассона.

26. Узагальнена модель системи масового обслуговування

Розглянемо загальні системи масового обслуговування, у яких існує як вхідний потік клієнтів, так і вихідний потік обслужених клієнтів. Час між послідовними надходженнями клієнтів і час обслуговування є експонентно розподіленими випадковими величинами.

При розгляді загальних систем масового обслуговування передбачається, що система функціонує протягом досить великого інтервалу часу, після закінчення якого в її роботі настає стаціонарний режим. Цей режим функціонування обслуговуючої системи протиставляється перехідному (або невстановленому) режимові, що превалює в самий початковий період функціонування системи.

У розглянутій нижче загальній моделі системи масового обслуговування передбачається, що і інтенсивність надходження клієнтів, і інтенсивність вихідного потоку залежать від стану системи, що означає їх залежність від числа клієнтів у системі обслуговування.

Введемо наступні позначення.

n – число клієнтів у системі обслуговування (у черзі і на обслуговуванні),

– інтенсивність надходження в систему клієнтів за умови, що в системі вже знаходиться n клієнтів,

– інтенсивність вихідного потоку обслужених клієнтів за умови, що в системі знаходиться n клієнтів,

– імовірність того, що в системі знаходиться n клієнтів.

У загальній моделі системи масового обслуговування встановлюється функціональна залежність імовірностей від і . Ці імовірності використовуються потім при визначенні функціональних характеристик обслуговуючої системи, таких як середня довжина черги, середній час очікування і середній коефіцієнт використання сервісів.

Імовірності визначаються з діаграми інтенсивностей переходів, представленої на рис. 7.3. Обслуговуюча система знаходиться в стані n, якщо в ній є n клієнтів. З аксіом пуассонівського процесу випливає, що імовірність появи більше одного нового клієнта протягом малого проміжку часу h прямує до нуля при h→0. Це означає, що при n>0 стан n може бути змінений в двох можливих напрямках: n–1, коли з інтенсивністю обслужений клієнт вибуває із системи, і n+1, коли має місце надходження клієнта з інтенсивністю . Стан 0 може змінитися лише до стану 1, коли має місце надходження клієнта з інтенсивністю . Зазначимо, що не визначене, оскільки не може відбуватися вибування клієнтів з порожньої системи обслуговування.

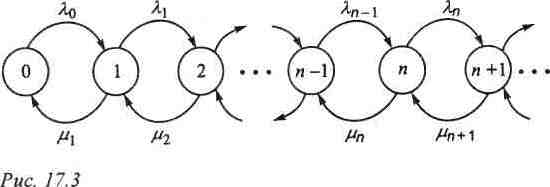
Рис. 7.3.

При виконанні умов стаціонарності очікувані інтенсивності вхідного і вихідного потоків у стані n (n>0) повинні бути рівні. Оскільки стан n може змінюватися лише до станів n–1 і n+1, то звідси випливає

.

Аналогічно,

Звідси, прирівнюючи ці дві інтенсивності, одержимо наступне рівняння балансу.

.

Як видно з рис. 7.3, рівняння балансу, що відповідає n=0, має вигляд

.

Рівняння балансу розв’язується рекурентно, послідовно виражаючи імовірності через наступним чином: для n=0 маємо

.

Далі, для n=1 одержимо

.

Підставляючи сюди і спрощуючи отриманий вираз, маємо (перевірте!)

.

Методом індукції можна показати, що

.

Значення визначається з рівняння .