16. Адаптація моделі економічного розміру замовлення до імовірнісної природи попиту

Деякі фахівці намагалися адаптувати детерміновану модель економічного розміру замовлення для урахування імовірнісної природи попиту, використовуючи при цьому наближений метод, що припускає існування постійного буферного запасу протягом усього планового періоду. Розмір резерву встановлюється таким чином, щоб імовірність виснаження запасу протягом періоду виконання замовлення не перевищувала наперед заданої величини.

Уведемо наступні позначення.

L – термін виконання замовлення, тобто час від моменту розміщення замовлення до його постачання;

– випадкова величина, що представляє величину попиту протягом терміну виконання замовлення;

– середня величина попиту протягом терміну виконання замовлення;

– середньоквадратичне відхилення величини попиту протягом терміну виконання замовлення;

B – розмір резервного запасу;

 – максимально можливе значення імовірності виснаження запасу протягом терміну виконання замовлення.

Основним припущенням при побудові моделі є те, що величина попиту протягом терміну виконання замовлення L є нормально розподіленою випадковою величиною із середнім і стандартним відхиленням , тобто має розподіл .

На рис. 6.1 показана залежність між розміром резервного запасу B і параметрами детермінованої моделі економічного розміру замовлення, що включає термін виконання замовлення L, середню величину попиту протягом терміну виконання замовлення й економічний розмір замовлення . Зазначимо, що L повинно дорівнювати ефективному часові виконання замовлення.

Імовірнісна умова, що визначає розмір резервного запасу B, має вигляд

.

За визначенням випадкова величина

є нормованою нормально розподіленою випадковою величиною, тобто має розподіл N(0,1). Отже,

.

На рис. 6.2 показана величина , що визначається з таблиці стандартного нормального розподілу, так що

.

Отже, розмір резервного запасу повинен задовольняти нерівності

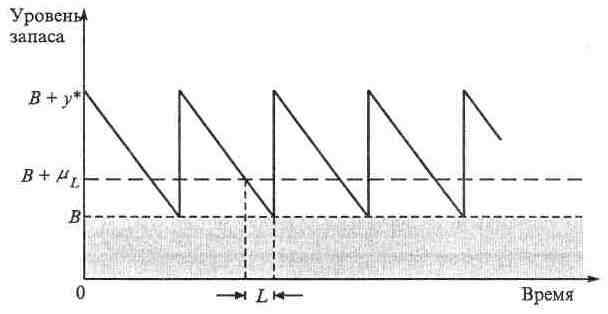
Рис. 6.1

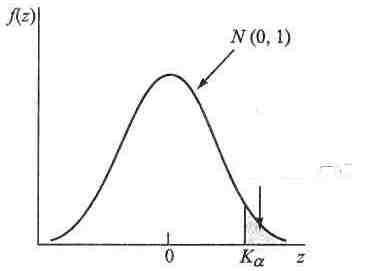
Рис. 6.2

Величина попиту протягом терміну виконання замовлення L звичайно описується щільністю розподілу імовірностей, віднесеної до одиниці часу (наприклад, до дня або тижня), з якої можна визначити розподіл попиту протягом періоду L. Зокрема, якщо попит за одиницю часу є нормально розподіленою випадковою величиною із середнім D і стандартним відхиленням , то загальний попит протягом терміну виконання замовлення L буде мати розподіл , де і . Формула для , отримана на підставі того, що значення L є цілим числом (або ж округлене до цілого числа).

17. Стохастичний варіант моделі економічного розміру замовлення

Немає підстав думати, що розглянута вище модель економічного розміру замовлення визначить оптимальну політику управління запасами. Підтвердженням цього є те, що істотна інформація, яка має відношення до імовірнісної природи попиту, при цьому підході спочатку не враховується, а використовується лише незалежно на останньому етапі обчислень. Щоб виправити цей недолік, розглянемо більш точну модель, у якій імовірнісна природа попиту враховується безпосередньо в постановці задачі.

На відміну від попереднього випадку у цій моделі допускається незадоволений попит, як це показано на рис. 6.3. У розглянутій моделі замовлення розміром y розміщається тоді, коли обсяг запасу досягає рівня R. Як і в детермінованому випадку, рівень R, при якому знову розміщається замовлення, є функцією періоду часу між розміщенням замовлення і його виконанням. Оптимальні значення y і R визначаються шляхом мінімізації очікуваних витрат системи управління запасами, віднесених до одиниці часу, що включають як витрати на розміщення замовлення і його збереження, так і втрати, пов'язані з незадоволеним попитом.

У розглянутій моделі прийняті три припущення.

1. Незадоволений протягом терміну виконання замовлення попит накопичується.

2. Дозволяється не більше одного невиконаного замовлення.

3. Розподіл попиту протягом терміну виконання замовлення є стаціонарним (незмінним) у часі.

Рис. 6.3

Для визначення функції, що відображає сумарні витрати, віднесені до одиниці часу, уведемо наступні позначення.

– щільність розподілу попиту x протягом терміну виконання замовлення;

D – очікуване значення попиту в одиницю часу;

h – питомі витрати на збереження (на одиницю продукції за одиницю часу);

p – питомі втрати від незадоволеного попиту (на одиницю продукції за одиницю часу);

K – вартість розміщення замовлення.

Ґрунтуючись на цих визначеннях, обчислимо компоненти функції витрат.

1. Вартість розміщення замовлень. Наближене число замовлень в одиницю часу дорівнює , так що вартість розміщення замовлень в одиницю часу дорівнює .

2. Очікувані витрати на збереження. Середній рівень запасу дорівнює

.

Отже, очікувані витрати на збереження за одиницю часу рівні .

Наведена формула отримана в результаті усереднення очікуваних запасів на початку та в кінці часового циклу, тобто величин і відповідно. При цьому ігнорується випадок, коли величина може бути від’ємною, що є одним із допущень, які спрощують розглядувану модель.

3. Очікувані втрати, які пов'язані з незадоволеним попитом. Дефіцит виникає при . Отже, очікуваний дефіцит за одиницю часу дорівнює

.

Оскільки в моделі передбачається, що p пропорційне лише обсягові дефіциту, очікувані втрати, які пов'язані з незадоволеним попитом, за один цикл дорівнюють . Оскільки одиниця часу містить циклів, то очікувані втрати, зумовлені дефіцитом, складають за одиницю часу.

Результуюча функція загальних втрат за одиницю часу TCU має такий вигляд.

.

Оптимальні значення і визначаються з представлених нижче рівнянь.

, .

Отже, маємо

, (1)

. (2)

Оскільки з рівнянь (1) і (2) і не можна визначити в явному вигляді, для їх знаходження використовується чисельний алгоритм, запропонований Хедлі й Уайтін (Hadley, Whitin). Доведено, що алгоритм збігається за скінченне число ітерацій при умові, що допустимий розв’язок існує.

При останні два рівняння відповідно дають наступне.

, .

Якщо , тоді існують єдині оптимальні значення для y і R. Обчислювальна процедура визначає, що найменшим значенням є , яке досягається при S=0.

Алгоритм складається з наступних кроків.

Крок 0. Приймаємо за початковий розв’язок і вважаємо . Кладемо i=1 і переходимо до кроку i.

Крок i. Використовуємо значення для визначення з рівняння (2). Якщо , обчислення припиняють; за оптимальний розв’язок приймаємо і . В іншому випадку, використовуючи значення з рівняння (1) знаходимо . Кладемо i=i+1 і повторюємо крок i.