
- •Оглавление
- •1. Количественные характеристики, используемые при измерении параметров вычислительных систем. Номинальное и пиковое быстродействие. Быстродействие вычислителя по гибсону.
- •2. Понятие о современных вычислительных системах. Диаметр. Средний диаметр.
- •3. Наиболее популярные схемы вычислительных систем: «общая шина», «линейка», «кольцо», «тор», «решетка».
- •4. Структура вычислительных систем типа двумерный тор, n-мерный двоичный гиперкуб.
- •5. Реализация обмена информацией в структуре типа «обобщенный nd-куб» и «nd-тор»
- •6. Структура вычислительных систем типа циркулянта и типа л(n,n,g) - граф.
- •7. Структура вычислительных систем типа «бинарное дерево», «мультидерево глубины n и ширины k».
- •8. Характеристика коммутаторов вычислительных систем.
- •9. Архитектурные свойства вычислительной сети и описание процессов её функционирования.
- •10. Надежность и живучесть вычислительной системы.
- •11А. Схемы обмена информацией между ветвями параллельных алгоритмов.
- •12. Структурные характеристики вычислительных систем.
- •13. Пример решения задачи умножения матриц с помощью вычислительных систем.
- •14. Показатели эффективности параллельных алгоритмов. Коэффициент накладных расходов, коэффициент ускорения. Понятие о сложных задачах.
- •Коэффициент ускорения
- •Понятие о сложных задачах
- •15. Закон амдаля и коэффициент эффективности параллельной программы.
- •16А. Понятие о сложных задачах
- •17. Принципы перехода от последовательного алгоритма к параллельному. Алгоритм преобразования последовательного алгоритма в параллельный.
- •18. Представление алгоритмов взвешенными графами. Свёртка и развёртка вершин графа. Основные определения матриц следования информационного графа. Алгоритмы их получения.
- •19. Треугольная матрица следования. Теорема об условиях её получения.
- •20. Матрица следования для информационно-логического графа. Алгоритм построения транзитивных связей в этой матрице.
- •21. Обоснование транзитивных операций дизъюнкции и конъюнкции.
- •22. Алгоритм определения наличия контуров в информационной граф-схеме алгоритма.
- •23. Понятие о матрице логической несовместимости. Внешние и внутренние замыкания в информационно-логическом графе.
- •24. Алгоритм построения матрицы логической несовместимости операторов.
- •25. Понятие о матрице независимости в граф-схемах алгоритмов.
- •26. Взаимно независимые операторы. Определение взаимной независимости. Полные и максимально полные множества взаимно независимых операторов.
- •27. Алгоритм нахождения полных множеств взаимно независимых операторов.
- •28. Алгоритмы построения ранних и поздних сроков окончания выполнения операторов.
- •29. Определение функции плотности загрузки и минимальной загрузки для вычислительных систем.
- •30. Алгоритм определения минимальной загрузки в вычислительной системе на заданном интервале.
- •31. Лемма об оценке максимально необходимого числа процессоров для решения поставленной задачи.
- •32. Утверждение об оценке минимально необходимого числа процессоров для решения поставленной задачи.
- •33. Об оценке снизу времени выполнения задачи при заданном количестве процессоров.
- •34. Уточнение оценки снизу времени выполнения задачи на n процессорах.
- •35. Алгоритм определения оценки минимального числа процессоров, необходимых для выполнения алгоритма за время t.
- •36. Алгоритм определения оценки минимального времени t выполнения заданного алгоритма на вычислительной системе, содержащей n процессоров.
- •37. Алгоритм оценки минимально необходимого количества процессоров для задачи, представленной информационно-логическим графом.
- •38. Алгоритм оценки времени выполнения задачи, представленной данным вычислительных систем графом.
- •39. Архитектурные аспекты при создании операционной системы вычислительных сетей.
- •40. Опыт применения методики крупноблочного распараллеливания сложных задач.
- •41. Основы функционирования вычислительной системы типа «микрос-т».
- •42. Исследование информационных графов с векторными весами вершин для планирования параллельных вычислений.
- •43. Алгоритм нахождения операторов входящих только в одно множество взаимно независимых операторов.
- •46. Определение плотности загрузки для I-го типа процессора и алгоритм ей вычисления.
- •51. Коммуникационная среда на основе масштабируемого когерентного интерфейcа sci.
- •52. Коммуникационная среда на основе технологии myrinet.
- •53. Краткая характеристика коммуникационной среды qsnet II.
- •54. Алгоритм распределения нитей граф-схемы алгоритма по узлам вычислительной сети.
- •55. Представление алгоритмов взвешенными графами. Основные определения матрицы описания информационного графа. Алгоритмы ее получения.
- •56. Изображение схем параллельных алгоритмов с помощью информационных (иг) и информационно-логических (илг) графов.
- •Вычисление матриц следования, расширенных матриц следования и матриц следования с транзитивными связями.
Структурная
живучесть:
![]()
![]() – это вероятность
существования подсистемы ранга r,
т.е. существуют подмножества ранга r
работоспособных вычислителей, связанность
которых устанавливается через
работоспособные линии связи.
– это вероятность
существования подсистемы ранга r,
т.е. существуют подмножества ранга r
работоспособных вычислителей, связанность
которых устанавливается через
работоспособные линии связи.
Структурная
живучесть
![]() характеризует приспособленность ВС к
условиям отказа вычислителей и линий
связи, к порождению системой тех или
иных рангов, следовательно, приспособленность
к решению задач заданной сложности.
характеризует приспособленность ВС к
условиям отказа вычислителей и линий
связи, к порождению системой тех или
иных рангов, следовательно, приспособленность
к решению задач заданной сложности.
Ищется
![]() при заданных значениях N,
r,
при заданных значениях N,
r,
![]() , S,
.
, S,
.
– количество связей в сети;
![]() –
оптимальная
структура.
–
оптимальная
структура.
Существуют
специальные решения для циркулянт и
Л-графов
![]() :
:
1.
обеспечивает max
![]()
2. Структура обладает наибольшей живучестью.
3. Структура оптимальна при заданном N, и имеет min диаметр.
13. Пример решения задачи умножения матриц с помощью вычислительных систем.
Будем считать, что система – полный граф.
![]()
![]() (1)
(1)
n – количество процессоров.
Исходные матрицы А, В разрезаются на n горизонтальных и вертикальных полос:
Т.о. для 1-го вычислителя:
Строки:
![]()
Столбцы:
![]()
Для L-го вычислителя:
Строки
![]()
Столбцы ![]()
n-й вычислитель:
строки ![]()
столбцы ![]()
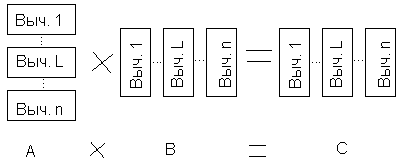
Параллельный
вычислительный процесс организуется
следующим образом: сначала первый
вычислитель передает остальным
вычислителям первую строку из своей
полосы матрицы А. После этого, все
вычислители используют формулу (1).
Осуществляется параллельный расчет
целой части
![]() элементов первой строки матрицы С. Затем
первый вычислитель рассылает всем
остальным вычислителям вторую строку
своей матрицы и производится расчет
элементов 2ой строки матрицы С и тд. До
тех пор пока 1ый вычислитель не перешлет
свои строки матрицы А. После этого
пересылками будут заниматься
последовательно 2ой, 3ий …nый
вычислители. Матрица получается
распределенной по вычислителям, причем
в каждом будет своя вертикальная полоса.
Вследствие однородного распределения
данных получены одинаковые ветви
параллельного алгоритма, однако эти
ветви используют различные части данных,
т.к. для каждой ветви своих данных
недостаточно, то ветви вступают во
взаимодействие.
элементов первой строки матрицы С. Затем
первый вычислитель рассылает всем
остальным вычислителям вторую строку
своей матрицы и производится расчет
элементов 2ой строки матрицы С и тд. До
тех пор пока 1ый вычислитель не перешлет
свои строки матрицы А. После этого
пересылками будут заниматься
последовательно 2ой, 3ий …nый
вычислители. Матрица получается
распределенной по вычислителям, причем
в каждом будет своя вертикальная полоса.
Вследствие однородного распределения
данных получены одинаковые ветви
параллельного алгоритма, однако эти
ветви используют различные части данных,
т.к. для каждой ветви своих данных
недостаточно, то ветви вступают во
взаимодействие.
Аналогичным образом решается итерационным методом система линейных уравнений:
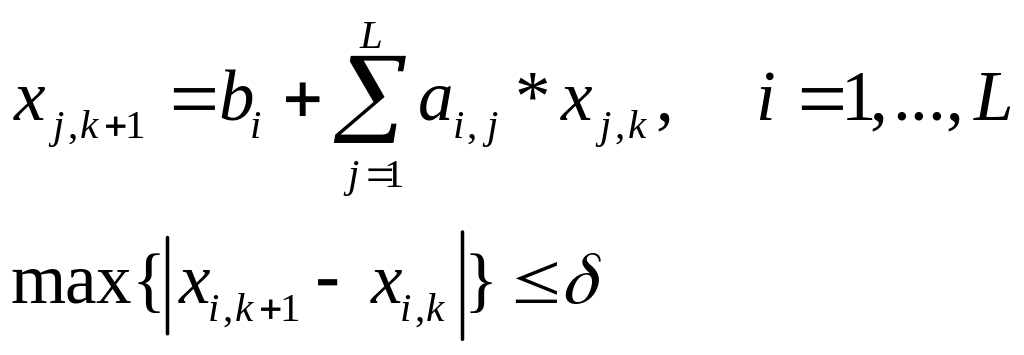
14. Показатели эффективности параллельных алгоритмов. Коэффициент накладных расходов, коэффициент ускорения. Понятие о сложных задачах.
1. Коэффициент
накладных расходов:
![]() ,
,
где t – время, расходуемое ВС на вспомогательные операции (организация обмена информацией, настройку вычислителей и д.р.);
T – время, требуемое на выполнение арифметической и логической операции при выполнении алгоритма.
Оценим эффективность умножения матриц:
![]() –
умножений
–
умножений
![]() –
сложений
–
сложений
Если К очень
большое, то эти величины приблизительно
равны
![]() .
.
![]() –
время пересылки
данных.
–
время пересылки
данных.
![]() - время сложения
двух чисел
- время сложения
двух чисел
![]() -
время умножения двух чисел
-
время умножения двух чисел
![]() следовательно,
max
накладных расходов, когда
следовательно,
max
накладных расходов, когда
![]() ,
т.е. M=n.
,
т.е. M=n.
Величина
![]() информирует о минимально-допустимом
размере матрицы, при которой еще можно
решать задачи на n-вычислителях.
Чем больше размер матрицы(чем больше
вычислений), тем больше эффективность
алгоритмов.
информирует о минимально-допустимом
размере матрицы, при которой еще можно
решать задачи на n-вычислителях.
Чем больше размер матрицы(чем больше
вычислений), тем больше эффективность
алгоритмов.
Коэффициент ускорения
![]() ,
где
,
где
![]() -
время выполнения алгоритма на одном
вычислителе,
-
время выполнения алгоритма на одном
вычислителе,
![]() -
время выполнения алгоритма на n
вычислителях.
-
время выполнения алгоритма на n
вычислителях.
 ,
где
,
где
![]() -
лучший последовательный алгоритм.
-
лучший последовательный алгоритм.
Понятие о сложных задачах
Представим коэффициент накладных расходов в развернутом виде:
![]()
V – Количество операций, которые необходимо выполнить при решении задачи на ВС.
n – Число вычислителей на ВС
![]()
k
– эмпирический коэффициент:
![]() ,
то задача считается сложной.
,
то задача считается сложной.
Задача называется сложной (трудоемкой, системной, с большим объемом вычислений), если число операций на несколько порядков превосходит количество процессоров.
15. Закон амдаля и коэффициент эффективности параллельной программы.
Закон Амдаля
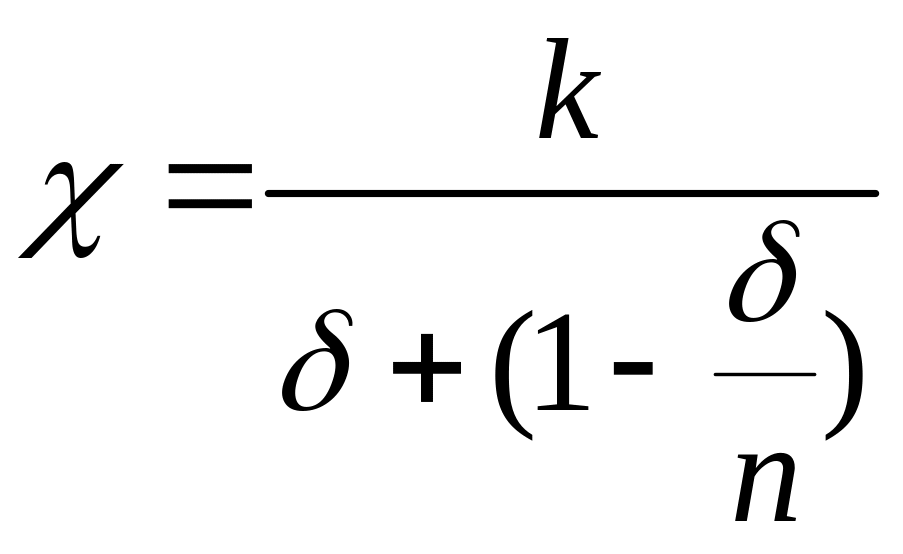 ,
где
,
где
n – количество вычислителей в системе;
![]() – относительная
доля операций параллельной программы,
выполненных последовательно :
– относительная
доля операций параллельной программы,
выполненных последовательно :![]() ;
;
![]() – программа
относительно последовательна;
– программа
относительно последовательна;
![]() –
программа
относительно параллельна;
–
программа
относительно параллельна;
k
– корректирующий коэффициент (![]() ),
определяет качество параллельной
системы. Сюда входит настройка структуры
системы, синхронизация ветвей параллельной
программы и временные издержки, связанные
с обменом информацией между вычислителями.
),
определяет качество параллельной
системы. Сюда входит настройка структуры
системы, синхронизация ветвей параллельной
программы и временные издержки, связанные
с обменом информацией между вычислителями.
(Х – это коэффициент ускорения)
Коэффициент эффективности параллельных программ.
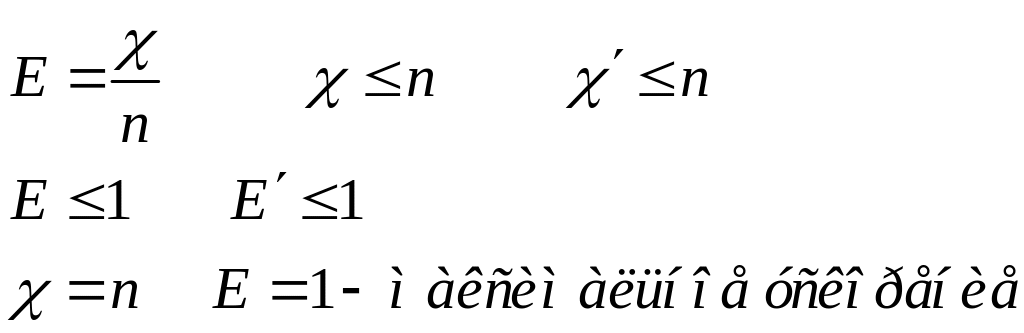 (при
Е=1 максимальное ускорение)
(при
Е=1 максимальное ускорение)
Причины по которым трудно достичь max ускорения:
1. время, расходуемое на синхронизацию процессов параллельных ветвей и организацию обмена информацией между ними. Конфликты памяти, обусловленные, например, ее общедоступностью или, наоборот, ее распределенностью.
2. несбалансированность нагрузки вычислителей и/или невозможность в общем случае построения параллельного алгоритма с числом ветвей, равных числу вычислителей ВС.
16А. Понятие о сложных задачах
Представим коэффициент накладных расходов в развернутом виде:
V – Количество операций, которые необходимо выполнить при решении задачи на ВС.
n – Число вычислителей на ВС
k – эмпирический коэффициент: , то задача считается сложной.
Задача называется сложной (трудоемкой, системной, с большим объемом вычислений), если число операций на несколько порядков превосходит количество процессоров.
17. Принципы перехода от последовательного алгоритма к параллельному. Алгоритм преобразования последовательного алгоритма в параллельный.
Параллельный алгоритм – это описание процесса обработки информации, ориентированного на реализацию с помощью вычислительных систем.
Представление параллельного алгоритма на языке программирования, доступном данной ВС, называется параллельной программой.
Существует 3 способа распараллеливания сложных задач:
Локальное. При локальном распараллеливании в выполняемой программе выделяются участки машинных команд, которые могут выполняться параллельно.
Глобальное. Глобальное распараллеливание происходит на уровне программных модулей.
Смешанное распараллеливание – наиболее эффективное, совмещает 1 и 2.
Приведение схем алгоритмов к виду, удобному для организации параллельных вычислений. При создании параллельных программ будем использовать схемы программ в соответствии с ГОСТ 19.003-80 ЕСПД, ГОСТ 19.701-90 ЕСПД, хотя следует отметить, что создание параллельных процессов в решаемых задачах и отображение их в таких схемах — достаточно трудоемкая работа. В связи с этим предложена следующая процедура создания параллельных схем алгоритмов или программ.
Вначале создается схема алгоритма, как это делалось для традиционных вычислительных средств без учета параллельных вычислений. Будем называть такие алгоритмы последовательными. Затем с помощью алгоритма преобразования последовательного алгоритма в параллельный на основе анализа зависимости участков процесса по обрабатываемым переменным выделяются параллельные ветви вычислений. Алгоритмы с выделенными параллельными ветвями и есть параллельные алгоритмы.
Введем несколько ограничений на изображение схем алгоритмов с параллельными ветвями:
При параллельном выполнении программ окончание алгоритма зависит от составленного плана решения задачи, поэтому символ «терминатор» конца алгоритма надо исключить.
Не ограничивая общности рассуждений, можно считать, что при изображении параллельных алгоритмов можно ограничиться логическим символом с двумя выходами: FALSE и TRUE.
Традиционное изображение вводимой информации в указанных ГОСТах более или менее приемлемо для ВС с общей памятью и совсем не приемлемо для ВС с разделяемой памятью, так как в этих ГОСТах вводится достаточно искусственная зависимость программных модулей по данным. Эта зависимость существенно сужает возможности распараллеливания решаемой задачи. При рассмотрении ВС с разделяемой памятью ввод-вывод информации включается в процесс обмена информацией между процессорами и таким образом учитывается в планировании вычислительного процесса. Поэтому при рассмотрении ВС с общим полем памяти считается, что вся исходная информация введена в поле общей памяти и на схеме не показывается.
Аналогично решаем проблему вывода. Выводимая информация также находится в поле общей памяти. Отсутствие символа вывода (например, параллелограмма) можно объяснить тем, что преобразование и вывод информации не включают в план решения параллельных задач. В связи с этим при преобразовании исходного алгоритма в параллельный опускают символы ввода-вывода информации.
Сущность алгоритма преобразования схемы последовательного алгоритма в схему параллельного алгоритма заключается в следующем:
Разобьем
последовательный алгоритм на линейные
участки, заключенные между логическими
операторами. Каждый логический
оператор порождает не менее двух линейных
участков. Линейный участок, образованный
входом в алгоритм и логическим оператором,
назовем начальным. Начальный участок
может содержать только один оператор.
Следующий за начальным участок начинается
и заканчивается логическим оператором,
т. е. если участок Ui,
состоит из
множества операторов
![]() ,
то следующий участок
,
то следующий участок
![]() и т. д., где
и т. д., где
![]() —
логические операторы, причем
—
логические операторы, причем
![]() ,
а
,
а
![]() —
некоторые операторы (не логические).
Таким образом, последний логический
оператор
—
некоторые операторы (не логические).
Таким образом, последний логический
оператор
![]() участка Ui,
является
первым оператором для участка Ui+1.
На каждом участке операторы
перенумерованы: 1,2, …, Uk.
Последние участки — это линейные
участки, не имеющие в качестве последнего
оператора логический оператор. Пусть
в результате такого разбиения образовалось
N участков
k
= 1,..., N,
в каждом из
которых оказалось Uk
операторов.
участка Ui,
является
первым оператором для участка Ui+1.
На каждом участке операторы
перенумерованы: 1,2, …, Uk.
Последние участки — это линейные
участки, не имеющие в качестве последнего
оператора логический оператор. Пусть
в результате такого разбиения образовалось
N участков
k
= 1,..., N,
в каждом из
которых оказалось Uk
операторов.
Назовем связи, входящие в вычислительный или логический блоки, входными; выходящие из этих блоков — выходными. Будем полагать, что в каждый блок может входить и выходить несколько связей. В анализируемом алгоритме для упрощения анализа зависимости рассматриваемого программного модуля от предыдущих принята следующая схема: анализируемый алгоритм представляет собой последовательность программных модулей (процедур и/или функций). Обмен данными между ними происходит только через параметры, указанные в списке при вызове модулей. Результаты работы модули передаются через параметры, формируемые как <имя параметра> ::=<префикс> <имя модуля>. Очевидно, что предлагаемое упрощение не является принципиальным и в случае необходимости легко можно учесть зависимости программных модулей по данным, осуществляемые с помощью понятий глобальных переменных различных уровней.
Алгоритм: Преобразование последовательного алгоритма в параллельный.
Разобьем последовательно алгоритм на N линейных участков: k = 1, ..., N, исключив при этом терминаторы начала, конца и ввода-вывода информации. Перенумеруем сначала участок при k=1: Uk= 1,... ,
 .
Так как первый блок является входом в
алгоритм, то положим МV
:= {1} —
множество входов в алгоритм.
.
Так как первый блок является входом в
алгоритм, то положим МV
:= {1} —
множество входов в алгоритм.Примем := 1.
Вычислим
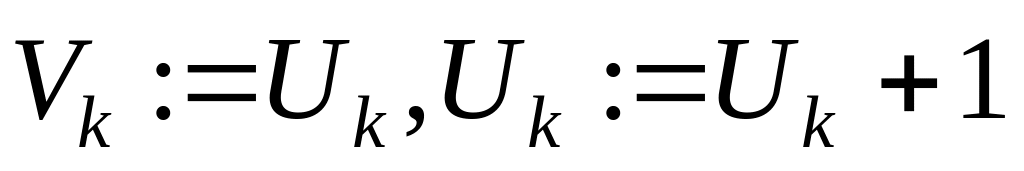 ,
Flag
:= False
(переменная Flag
фиксирует
проведение очередной связи).
,
Flag
:= False
(переменная Flag
фиксирует
проведение очередной связи).Если
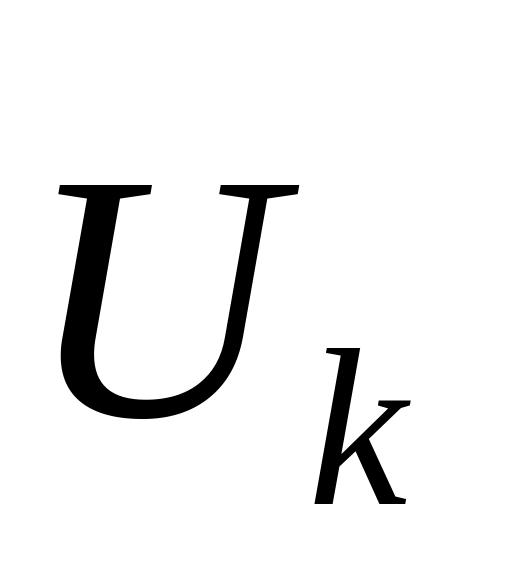 >
,
то проверим, все ли блоки имеют выходные
связи. Если да, то переходим к шагу 7,
иначе проведем связи из блоков, не
имеющих выходных связей, в блок
и
перейдем к шагу 7. Если
≤
,
то выполняется следующий шах.
>
,
то проверим, все ли блоки имеют выходные
связи. Если да, то переходим к шагу 7,
иначе проведем связи из блоков, не
имеющих выходных связей, в блок
и
перейдем к шагу 7. Если
≤
,
то выполняется следующий шах.Если блок использует результаты работы блока
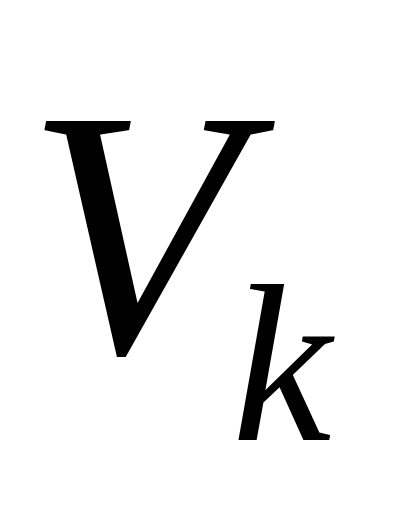 ,
то проведем связь из блока
в
,
положим
Flag
:= True
и перейдем к
шагу 3. Иначе
выполняется следующий шаг.
,
то проведем связь из блока
в
,
положим
Flag
:= True
и перейдем к
шагу 3. Иначе
выполняется следующий шаг.Вычислим
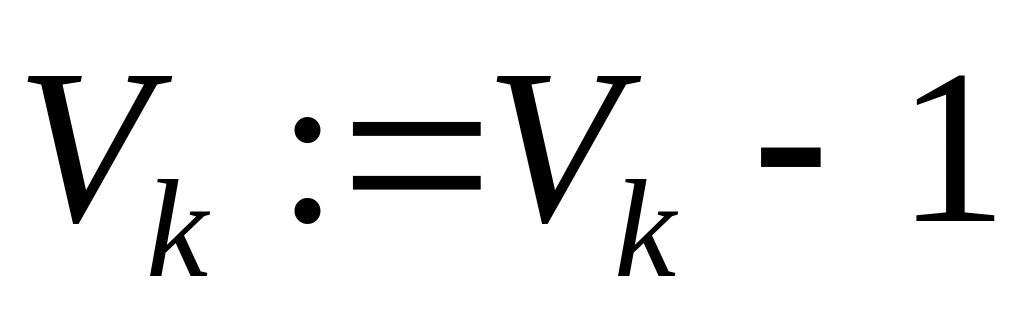 .
Если
.
Если
 ,
то переходим к шагу 5, иначе, если k=1
и Flag
:= False,
принимаем
как еще один
вход в алгоритм
,
то переходим к шагу 5, иначе, если k=1
и Flag
:= False,
принимаем
как еще один
вход в алгоритм
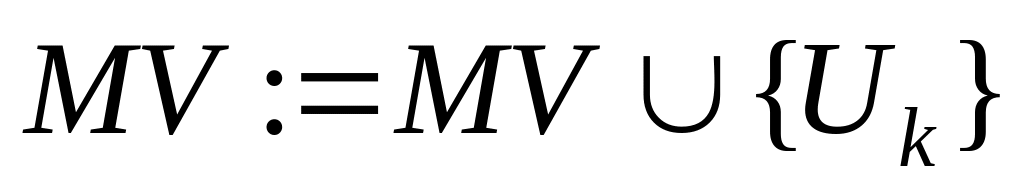 .
Если k
> 1 и Flag
:= False,
то проводим связь из блока
.
Если k
> 1 и Flag
:= False,
то проводим связь из блока
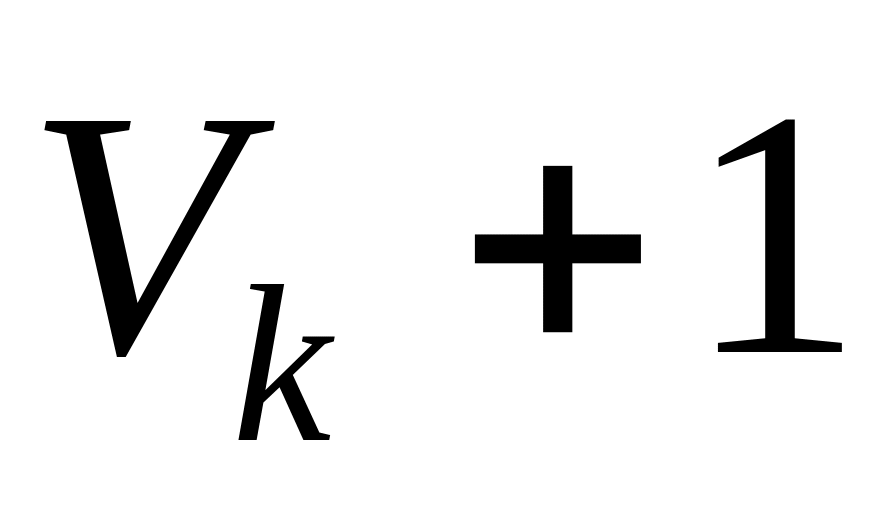 в
.
Переходим к шагу 3.
в
.
Переходим к шагу 3.Вычислим k:= k + 1. Если k > N, то определяется коней алгоритма, иначе переходим к шагу 2
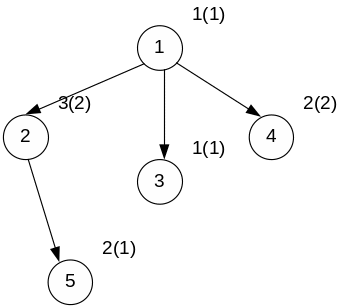
18. Представление алгоритмов взвешенными графами. Свёртка и развёртка вершин графа. Основные определения матриц следования информационного графа. Алгоритмы их получения.
Информационный, или информационно-логический граф задается с помощью выражения
G = (X,P,D), где X={i} = {1. ..., m} — множество вершин графа, соответствующее множеству операторов параллельного алгоритма, Р={pi}, i =1. ..., m; pi — множество весов, определяющих время выполнения каждого i-го оператора. В общем случае pi — вектор. Размерность вектора равна количеству типов процессоров, используемых в неоднородной ВС. Для однородной ВС pi — скаляр, а D — множество дуг графа. Дуги бывают двух типов:
![]() .
.
Дуги
![]() назовем
информационными. Эти дуги соответствуют
связям, исходящим из исполнительных
блоков параллельного алгоритма.
Информационно-логические дуги
назовем
информационными. Эти дуги соответствуют
связям, исходящим из исполнительных
блоков параллельного алгоритма.
Информационно-логические дуги
![]() соответствуют
связям, исходящим из логических блоков.
Дуги
нагружены
меткой Т для
связей, соответствующих логическому
значению TRUE,
и F
для связей
со значением FALSE.
соответствуют
связям, исходящим из логических блоков.
Дуги
нагружены
меткой Т для
связей, соответствующих логическому
значению TRUE,
и F
для связей
со значением FALSE.
Граф, содержащий
только дуги из множества D1,
называется
информационным
графом,
или информационной граф-схемой алгоритма.
Граф, содержащий некоторые дуги
![]() (в частном
случае — все), называется
информационно-логическим
графом,
или информационно-логической граф-схемой
алгоритма.
(в частном
случае — все), называется
информационно-логическим
графом,
или информационно-логической граф-схемой
алгоритма.
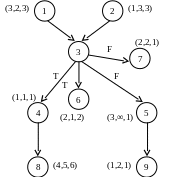
ИГ: ИЛГ:
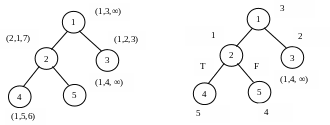
Нумерация в кружке – имя процедуры (номер вершины).
Скобки – вектора весов (тут 3х-мерные вектора)
Номер позиции – тип процессора.
∞ - на этом процессоре данная процедура не выполняется.
Если в параллельном
алгоритме существует связь между
операторами
![]() ,
,![]() и
— исполнительный блок, то в графе G
существует
дуга
и
— исполнительный блок, то в графе G
существует
дуга
![]() ,
исходящая из
вершины
и входящая в вершину
.
Эту связь будем обозначать
,
исходящая из
вершины
и входящая в вершину
.
Эту связь будем обозначать
![]() и
называть информационной
связью.
и
называть информационной
связью.
Если в параллельном
алгоритме существует связь между
операторами
,
и
— логический блок, то в графе G
существует
дуга
исходящая
из вершины
и входящая в вершину
.
Эту связь будем обозначать
![]() для
дуги с меткой Т
и
для
дуги с меткой Т
и
![]() для дуги с меткой F
и называть
связью
по управлению.
для дуги с меткой F
и называть
связью
по управлению.
Связи , , называют задающими связями.
Путями
в графе G
назовем
последовательности вершин
![]() ,
такие, что для любой пары вершин
,
такие, что для любой пары вершин
![]() существует дуга
существует дуга
![]() ,
исходящая
из вершины
,
исходящая
из вершины
![]() ,
и входящая в вершину
,
и входящая в вершину
![]() .
.
В графе G нет циклов, поэтому все пути имеют конечную длину. Кроме того, будем считать, что значения логических переменных для различных логических операторов не связаны друг с другом, поэтому в процессе реализации алгоритма возможен любой из допустимых путей.
Длиной пути в графе G назовем количество вершин, входящих в этот путь.
Характеристикой пути в графе G со скалярными весами вершин назовем сумму весов вершин, составляющих этот путь.
Путь с максимальной характеристикой Ткр в графе G со скалярными весами вершин назовем критическим. В одном графе может быть несколько критических путей.
В качестве формального средства обработки графов введем матрицу следования S (транспонированная матрица смежности). В матрице следования для удобства использования в столбцах помечены ненулевым значением все выходящие из данной вершины связи, а в строках — все входящие в данную вершину связи.
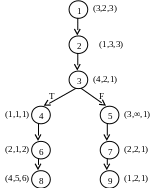
Более точное определение
матрицы следования заключается в
следующем: i
–ой вершине
графа G
ставятся в соответствие i
– ые столбец и
строка матрицы, если существует связь
по управлению
![]() ,
то элемент матрицы равен (i,j)
= jT,
,
то элемент матрицы равен (i,j)
= jT,
![]() порождает значение (i,j)
= jF,
при j
→ i образуется
(i,j)
= 1. Остальные
элементы матрицы равны 0.
порождает значение (i,j)
= jF,
при j
→ i образуется
(i,j)
= 1. Остальные
элементы матрицы равны 0.
1 |
|
|
|
|
|
|
|
|
|
3 |
2 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|
3 |
2 |
3 |
2 |
1 |
|
|
|
|
|
|
|
|
1 |
3 |
3 |
|
2 |
|
|
|
|
|
|
|
|
|
1 |
3 |
3 |
3 |
|
1 |
|
|
|
|
|
|
|
4 |
2 |
1 |
|
3 |
1 |
1 |
|
|
|
|
|
|
|
4 |
2 |
1 |
4 |
|
|
3T |
|
|
|
|
|
|
1 |
1 |
1 |
|
4 |
|
|
3T |
|
|
|
|
|
|
1 |
1 |
1 |
5 |
|
|
3F |
|
|
|
|
|
|
3 |
∞ |
1 |
|
5 |
|
|
3T |
|
|
|
|
|
|
3 |
∞ |
1 |
6 |
|
|
|
1 |
|
|
|
|
|
2 |
1 |
2 |
|
6 |
|
|
3F |
|
|
|
|
|
|
2 |
1 |
2 |
7 |
|
|
|
|
1 |
|
|
|
|
2 |
2 |
1 |
|
7 |
|
|
3F |
|
|
|
|
|
|
2 |
2 |
1 |
8 |
|
|
|
|
|
1 |
|
|
|
4 |
5 |
6 |
|
8 |
|
|
|
1 |
|
|
|
|
|
4 |
5 |
6 |
9 |
|
|
|
|
|
|
1 |
|
|
1 |
2 |
1 |
|
9 |
|
|
|
|
|
1 |
|
|
|
1 |
2 |
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
Расширенные матрицы SR следования для
а) последовательного алгоритма и б) параллельного алгоритма
19. Треугольная матрица следования. Теорема об условиях её получения.
Рассмотрим условие получения матриц следования в треугольном виде. По условию граф-схемы не должны содержать циклов (контуров). Это означает, что главная диагональ всегда должна содержать нулевые элементы.
Найдем условие
построения треугольной матрицы следования
для граф-схемы без цикла. Введем в
граф-схемы понятие яруса. Возьмем
произвольную вершину
в графе G,
Найдем все
длины путей, ведущих в
.
Среди этих длин найдем максимальную:
пусть это будет число
![]() .
Аналогичные
вычисления выполним для некоторой
вершины
и получим
.
Аналогичные
вычисления выполним для некоторой
вершины
и получим
![]() .
.
Если,
![]() то вершины
и
принадлежат одному ярусу - ярусу
h.
то вершины
и
принадлежат одному ярусу - ярусу
h.
Для обеспечения получения треугольной матрицы следования для графа G необходимо при нумерации вершин придерживаться следующего правила: вершины, принадлежащие (d + 1)-му ярусу, должны иметь номера большие, чем номера вершин d-ro яруса. Внутри одного яруса вершины могут нумероваться произвольно. Такую нумерацию назовем нумерацией по ярусам.
Матрица следования получится треугольной, если в граф-схеме G произведена нумерация по ярусам.
Предположим, что в некоторой строке δ матрицы следования существует ненулевой элемент правее главной диагонали. Это значит, что существует связь δ+v→δ. Т.к. номер δ+v>δ, то dδ ≤ dδ+v по условию построения матрицы S. Однако, любой путь в вершину δ+v может быть продолжен в вершину δ, поэтому dδ > dδ+v, что противоречит предыдущему неравенству. Элемент v был выбран произвольно, следовательно, утверждение теоремы справедливо для любого элемента, лежащего левее главной диагонали.
20. Матрица следования для информационно-логического графа. Алгоритм построения транзитивных связей в этой матрице.
При решении задачи распараллеливания важную роль играют не только задающие связи, но и так называемые транзитивные.
Если вершины
и
![]() связаны
задающими связями, то существует
транзитивная связь
связаны
задающими связями, то существует
транзитивная связь
![]() .
.
Множество связей, которые введены направленно внутри всех пар элементов, принадлежащих одному пути в графе G и не связанных задающими связями, назовем множеством транзитивных связей для заданного пути.
Множество транзитивных связей графа G есть объединение множеств транзитивных связей но всем путям графа G.
Множество
транзитивных связей, очевидно, полностью
определяется множеством задающих
связей. При формировании множества
транзитивных связей следует учитывать,
что если
и
![]() ,
где
,
где
![]() —
множество всех операторов, связанных
с оператором
,
то все операторы
—
множество всех операторов, связанных
с оператором
,
то все операторы
![]() связаны
транзитивно с оператором
.
связаны
транзитивно с оператором
.
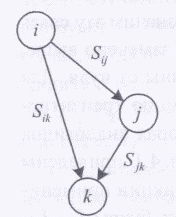
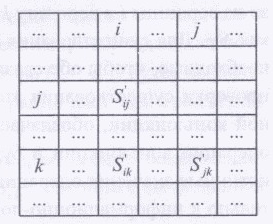
Рассмотрим построение матрицы следования с транзитивными связями St- Возьмем три произвольные вершины i, j, k такие, что между ними определены следующие связи: связь вершины i с вершиной j, вершины j с вершиной k, вершины i с вершиной k, как показано на рис:
В матрице следовании,
изображенной на рисунке, многоточием
обозначены другие связи, которые для
данного случая не представляют
интереса. При построении матрицы S
элементы
матрицы, соответствующие логическим
связям, выписываются по формуле
![]() ,
а информационным — по формуле
,
а информационным — по формуле
![]() .
.
Алгоритм. Построение матрицы следования с транзитивными связями.
Вычислим St:=S.
В матрице следования SТ размера RS просмотрим строки, начиная с первой.
Если в очередной i-й строке матрицы St отыскивается элемент (i, j)≠0, то вычислим значения элементов (i, 1), ..., (i, j-1) матрицы St для k = 1,..., j-1, используя соотношение
![]()
4.Вычислим j := j + 1. Если j ≤ RS, то переходим к шагу 3, иначе — работа алгоритма заканчивается (просмотрены все строки).
Конец алгоритма.
21. Обоснование транзитивных операций дизъюнкции и конъюнкции.
При построении транзитивных связей необходимо произвести анализ значений типов связей между этими вершинами и определить, какую связь между вершинами i и k выбрать: непосредственную или через вершину j. (для построения матрицы следования с транзитивными связями)
Первое, что влияет на этот выбор - это наличие транзитивной связи из вершины i в вершину k через вершину j. Обозначим эту связь ST. Для существования такой связи, как было замечено выше, необходимо, чтобы обе связи Sij и Sjk были отличны от нуля. Для проверки этой связи введем операцию «Ä», которая аналогична операции конъюнкции в булевой алгебре. Таблица истинности операции «Ä» применительно к информационно-логическим графам представлена в таблице:
Sij |
Sjk |
Sik = SijÄSjk |
0 0 0 1 1 L1 |
0 1 L 1 L L2 |
0 0 0 1 L L1_ L2 |
Sik |
SТ |
Sik Å SТ |
0 0 0 1 1 L1 |
0 1 L L 1 L2 |
0 1 L L 1 L1_ L2 |
Таким образом, для трех рассматриваемых вершин можно определить новую связь, используя две введенные операции, т.е. связь Sik можно вычислить по следующей формуле: Sik=SikÅ(SijÄSjk) (2)
или применительно к матрице следования : (k,i)=(k,i) Å ((j,i) Ä(k,j)) (3)
После последовательного преобразования всей S мы получим матрицу ST.
22. Алгоритм определения наличия контуров в информационной граф-схеме алгоритма.
Алгоритм использует свойство появления ненулевого элемента в главной диагонали матрицы ST. В качестве исходной берется нетреугольная матрица S. Поэтому при получении транзитивных связей предыдущий алгоритм вызывается несколько раз до получения неизменяемой матрицы Sт.
Алгоритм. Определение контуров в граф-схеме алгоритма.
Вычислим матрицу
 .
.С помощью алгоритма «построения матрицы следования с транзитивными связями», используя матрицу Sт, вычислим матрицу
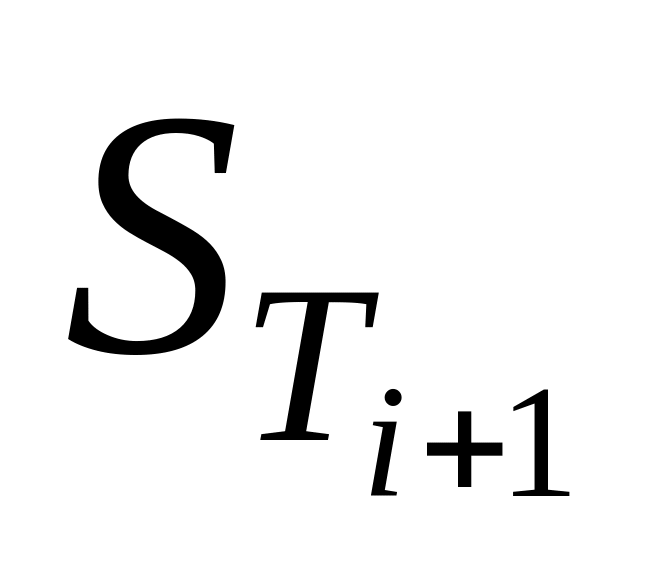 -
-На главной диагонали матрицы определим, есть ли ненулевые элементы. Если есть, то исследуемый граф имеет цикл и работа алгоритма завершена. В противном случае проверяем, изменилась ли матрица . Если
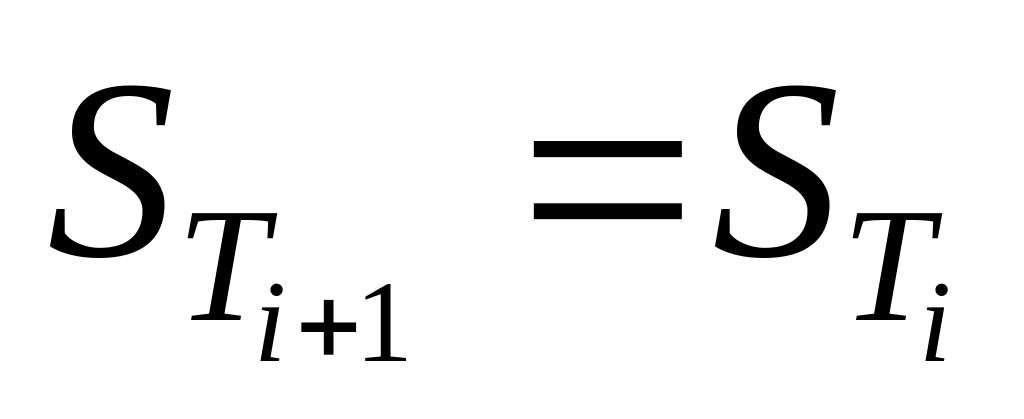 ,
то исследуемый граф не имеет контуров.
Алгоритм заканчивает работу. Иначе
определим
,
то исследуемый граф не имеет контуров.
Алгоритм заканчивает работу. Иначе
определим
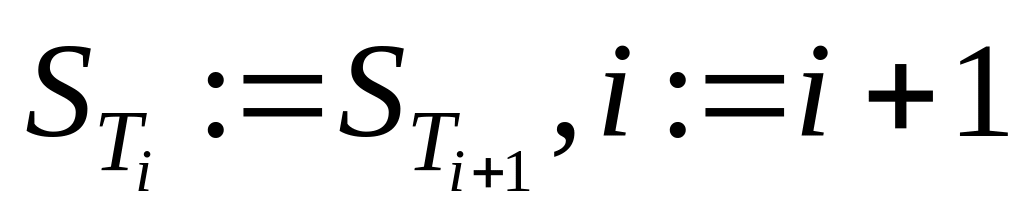 и осуществим
переход к шагу 2.
и осуществим
переход к шагу 2.
Конец алгоритма.
23. Понятие о матрице логической несовместимости. Внешние и внутренние замыкания в информационно-логическом графе.
При оценке возможности параллельного выполнения программных модулей важную роль играют логически несовместимые операторы. Рассмотрим множество вершин, принадлежащих ветви Т i-го логического оператора. Это множество назовем МTi. Аналогично построим множество вершин для дуги F — это множество вершин, принадлежащих ветви F i-го логического оператора множество MFi. В множества МTi и MFi сама вершина i не входит.
Если вершина
![]() j
и могут
выполняться либо один, либо другой
соответствующие им операторы при
однократном выполнении алгоритма, то
эти операторы называются логически
несовместимыми.
j
и могут
выполняться либо один, либо другой
соответствующие им операторы при
однократном выполнении алгоритма, то
эти операторы называются логически
несовместимыми.
При реализации
алгоритма в логическом операторе i
выполняется
либо ветвь Т,
либо ветвь
F,
Следовательно,
при планировании параллельных вычислений
надо исключать планирование параллельного
выполнения операторов, принадлежащих
разным ветвям, т.е. попросту исключить
их из планирования. Однако встречаются
ситуации, когда ветви F
и Т
пересекаются,
т. е.
![]() .
.
Е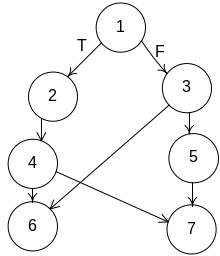 сли
сли
![]() ,
то существует внутреннее
замыкание
i-го
логического оператора. В
этом случае операторы
,
то существует внутреннее
замыкание
i-го
логического оператора. В
этом случае операторы
![]() ,
могут
планироваться для параллельного
выполнения. Вершина
,
могут
планироваться для параллельного
выполнения. Вершина
![]() имеющая
наименьший номер, называется
минимальной
внутренне замкнутой вершиной
i-гo
логического оператора и обозначается
inzi
имеющая
наименьший номер, называется
минимальной
внутренне замкнутой вершиной
i-гo
логического оператора и обозначается
inzi
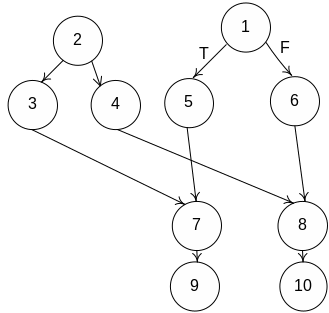 Следует
отметить, что замыкание логических
путей может осуществляться за счет
внешних информационных связей.
Целесообразно рассмотреть внешнее
замыкание для ветвей Т
и
F
отдельно.
Это связано с тем, что при рассмотрении
возможности параллельного выполнения
операторов, включенных в логические
ветви, необходимо учитывать результаты
как внешнего, так и внутреннего
замыканий совместно, имея в виду при
этом, что возможно внешнее замыкание
только одной ветви.
Следует
отметить, что замыкание логических
путей может осуществляться за счет
внешних информационных связей.
Целесообразно рассмотреть внешнее
замыкание для ветвей Т
и
F
отдельно.
Это связано с тем, что при рассмотрении
возможности параллельного выполнения
операторов, включенных в логические
ветви, необходимо учитывать результаты
как внешнего, так и внутреннего
замыканий совместно, имея в виду при
этом, что возможно внешнее замыкание
только одной ветви.
Если существует
информационный путь в вершину
![]() от
начальной вершины граф-схемы, то вершина
Z
называется
внешне замкнутой в ветви Т
для i-го
логического оператора. Если таких
вершин несколько, то вершину Z
с минимальным
номером называют минимальной
внешне замкнутой вершиной
в ветви Т
для i-го
логического оператора. Обозначим
эту вершину как ezTi
= Xi.
Аналогично
определяется внешнее замыкание ветви
F,
обозначающееся
ezFi.
от
начальной вершины граф-схемы, то вершина
Z
называется
внешне замкнутой в ветви Т
для i-го
логического оператора. Если таких
вершин несколько, то вершину Z
с минимальным
номером называют минимальной
внешне замкнутой вершиной
в ветви Т
для i-го
логического оператора. Обозначим
эту вершину как ezTi
= Xi.
Аналогично
определяется внешнее замыкание ветви
F,
обозначающееся
ezFi.
Если множество
![]() содержит внешнее замыкание ezT=xj,
то подмножество
содержит внешнее замыкание ezT=xj,
то подмножество
![]() называется
внешне
замкнутым для ветви Т
логического
оператора Li.
Если
множество
называется
внешне
замкнутым для ветви Т
логического
оператора Li.
Если
множество
![]() содержит внешнее замыкание ezF=xj,
то подмножество
содержит внешнее замыкание ezF=xj,
то подмножество
![]() называется
внешне
замкнутым для ветви F
логического
оператора Li.
называется
внешне
замкнутым для ветви F
логического
оператора Li.
При рассмотрении влияния внешних и внутренних замыканий на оценку возможности распараллеливания операторов необходимо учесть:
— что для распараллеливания операторов, принадлежащих путям логического оператора, достаточно одного внешнего замыкания при наличии внутреннего;
что внутреннее замыкание, как правило, порождает операторы, которые можно выполнять параллельно; что для определения множества MZi, всех замкнутых операторов i-го логического оператора требуется вычислить объединение множеств
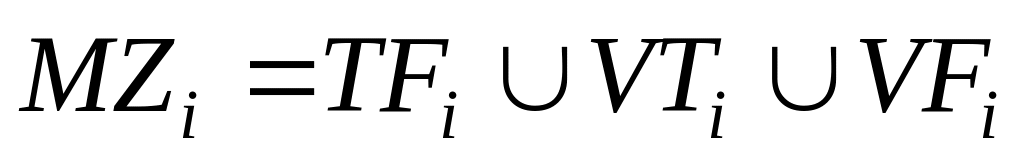 ;
;
24. Алгоритм построения матрицы логической несовместимости операторов.
S – матрица следования; RS – размерность матрицы S; ST – матрица с транзитивными связями; RST – размерность матрицы ST; MLO – множество логических операторов; RMLO – размерность множества логических операторов. M – множество вершин операторов; MTk – множество вершин операторов, включающим дугу Т k-го оператора; VFk – множество вершин операторов, внешне замкнутых для k-го логического оператора связи F; MFk – множество вершин операторов, включающим дугу F k-го оператора; RMTk – размерность множества логических операторов ветви Т; RMFk – размерность множества логических операторов ветви F; TFk – множество вершин операторов, внутренне замкнутых для k-го логического оператора; VTk – множество вершин операторов, внешне замкнутых для k-го логического оператора связи Т; MZk – объединенное множество внешних и внутренних замыканий для k-го логического оператора.
А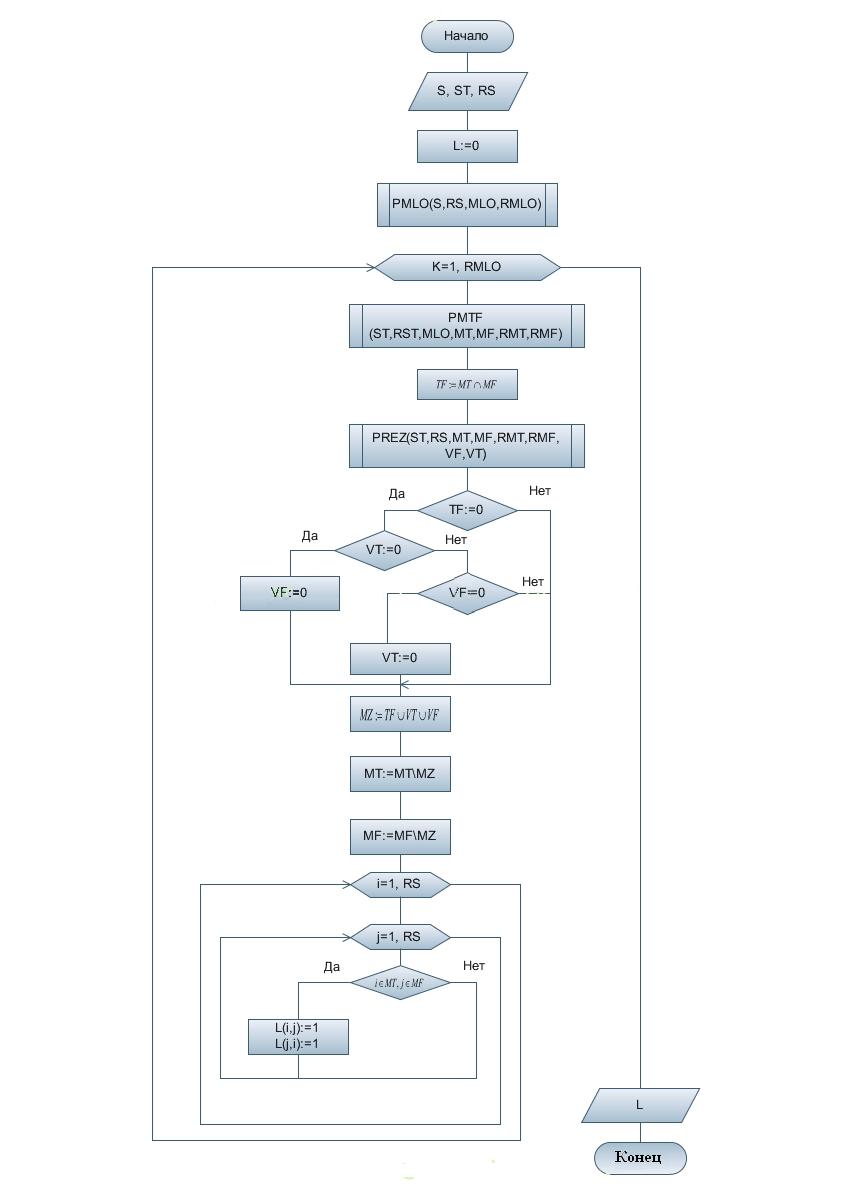 лгоритм
PMLO
. Получение множества логических
операторов.
лгоритм
PMLO
. Получение множества логических
операторов.
1. В матрице S размера RS выберем первый столбец (j : = 1), RMLO := 0, MLO := Ø.
Просмотрим j-й столбец по строкам и определим равенство текущего элемента матрицы jT или jF.
Если найден такой элемент, то положим
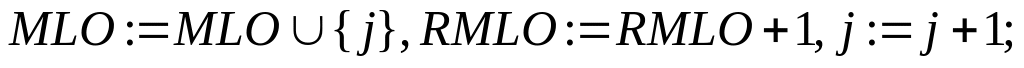 .
.
4.Если j ≤ RS, то перейдем к шагу 2, иначе конец алгоритма. Конец алгоритма.
Алгоритм PMTF. Получение множества МТ и MF k-то логического оператора
В соответствии со значением k выберем элемент множества
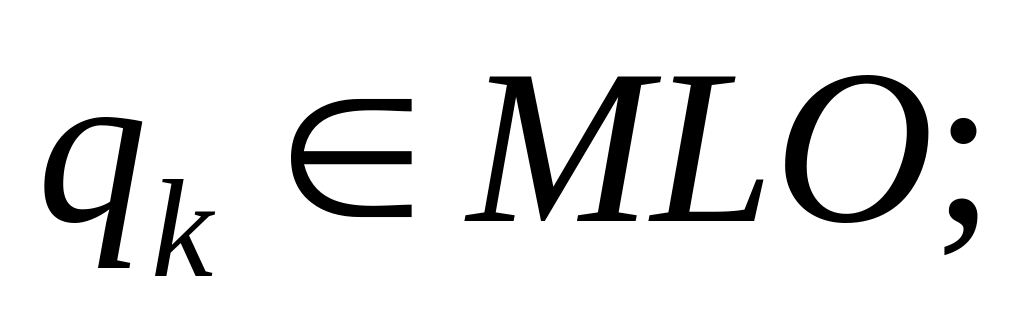 .
В
.
В
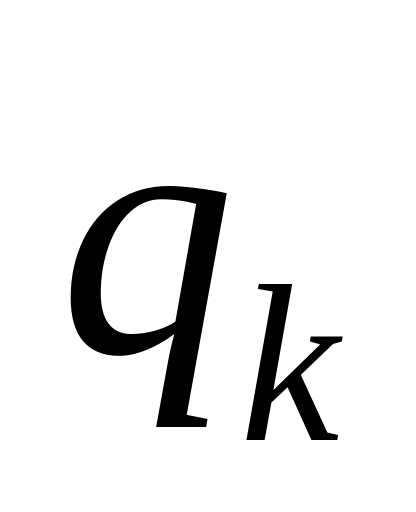 -м
столбце матрицы St
просмотрим
i-e
строки.
Положим i:=
1 (номер строки), l
:= 1 (номер
позиции в множестве МТ),
m
:= 1 (номер
позиции в множестве MF).
-м
столбце матрицы St
просмотрим
i-e
строки.
Положим i:=
1 (номер строки), l
:= 1 (номер
позиции в множестве МТ),
m
:= 1 (номер
позиции в множестве MF).Если элемент матрицы ST(i, k)=jT, то MT[l]:= i, l=l+ 1; осуществим переход к шагу 5.
Если ST(i, k)=jF, то MF[m]:= i; m:=m + 1; выполним шаг 5.
Если условия пунктов 2 и 3 не выполняются, то осуществим переход к шагу 5.
Вычислим i:=i + 1. Если i > RST, то RMT:=l, RMF:=m и выполнение алгоритма заканчивается. Иначе осуществим переход к шагу 2.
Конец алгоритма.
Алгоритм PREZ. Формирование множества внешних замыканий.
1. Сформируем множество из номеров нулевых строк матрицы St: ZS:={i1,..., iq}. Положим VT:= Ø, VF :=Ø..
Для всех элементов
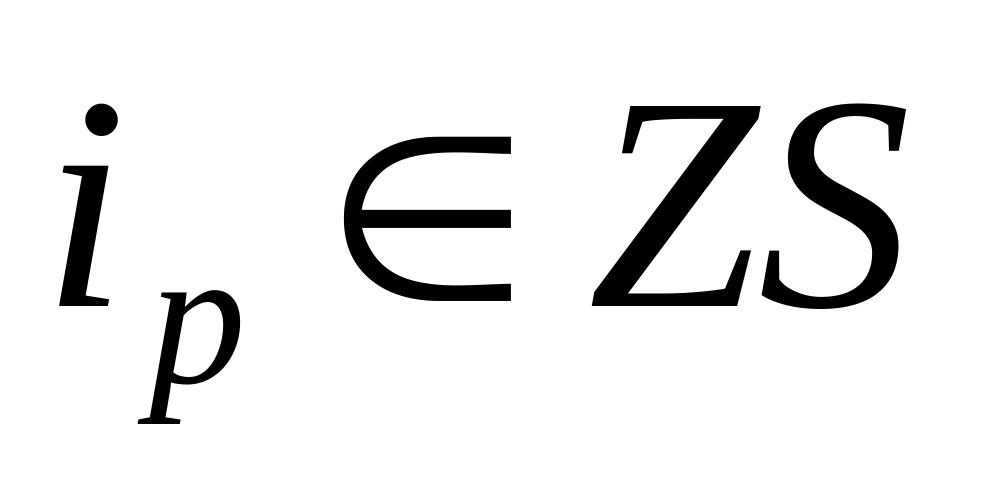 построим
множество EDp
номеров
строк, содержащих единичные элементы
в ip
столбцах.
построим
множество EDp
номеров
строк, содержащих единичные элементы
в ip
столбцах.Исключим из множества EDp, р = 1,..., q элементы, равные номеру рассматриваемою логического оператора k. Перенумеруем множества EDP, учитывая удаленные элементы. Получим множества EDu, и = 1, ...,f, f< q. Если все EDu = 0, то VT:= Ø, VF :=Ø.
Вычислим множества VT
 где
МT
и MF
— множества операторов для текущего
вложенного оператора.
где
МT
и MF
— множества операторов для текущего
вложенного оператора.
Конец алгоритма.
25. Понятие о матрице независимости в граф-схемах алгоритмов.
Для определения возможности распараллеливания операторов необходимо провести анализ независимости операторов по данным и по управлению. Для этих целей вводится матрица независимости операторов М.
Симметричная
матрица
![]() ,
где
,
где
![]() — операция
дизъюнкции булевой алгебры;
— операция
дизъюнкции булевой алгебры;
![]() ,
если
,
если
![]() ,
и
,
и
![]() ,
если
,
если
![]() для
i
=1, ...,RST
и j
= 1, ... , RST
(не треугольная, а получается зеркальным
отображением относительно главной
диагонали из ранее полученной треугольной);
L(i,j)
—- матрица
логической несовместимости, называется
матрицей независимости операторов.
для
i
=1, ...,RST
и j
= 1, ... , RST
(не треугольная, а получается зеркальным
отображением относительно главной
диагонали из ранее полученной треугольной);
L(i,j)
—- матрица
логической несовместимости, называется
матрицей независимости операторов.
Матрица М отражает информационно-логические связи между операторами без учета их ориентации и с учетом транзитивных связей и логической несовместимости операторов.
Следует отметить, что в соответствии с определением для информационного графа матрица М совпадает с матрицей S'.
Операторы
![]() и
и
![]() - взаимно независимые (ВНО), если в матрице
независимости
- взаимно независимые (ВНО), если в матрице
независимости
![]() .
.
Операторы
![]() ,
,
![]() ,
образуют полное множество ВНО, если для
любого оператора
,
образуют полное множество ВНО, если для
любого оператора
![]() существует пара элементов матрицы
независимости
существует пара элементов матрицы
независимости
![]() ,
,
![]() .
.
Множество, содержащее наибольшее число элементов для данного графа, называется максимально полным.
Пусть некоторый алгоритм представлен информационно-логической граф-схемой. По нулевым элементам матрицы независимости М в строке каждого оператора можно указать множество тех операторов, каждый из которых при выполнении некоторых условий может быть выполнен одновременно с данным, т.е. он информационно или по управлению не зависит от данного и не является с ним логически несовместимым.
26. Взаимно независимые операторы. Определение взаимной независимости. Полные и максимально полные множества взаимно независимых операторов.
Операторы и — взаимно независимые (ВНО), если в матрице независимости М ( , ) = М ( , ) = 0.
Операторы
![]() образуют
полное
множество
ВНО, если для любого оператора
образуют
полное
множество
ВНО, если для любого оператора
![]() существует пара элементов матрицы
независимости
существует пара элементов матрицы
независимости
![]()
Множество, содержащее наибольшее число элементов для данного графа, называется максимально полным.
По нулевым элементам матрицы независимости М в строке каждого оператора можно указать множество тех операторов, каждый из которых при выполнении некоторых условий может быть выполнен одновременно с данным, т. е. он информационно или по управлению не зависит от данного и не является с ним логически несовместимым.
27. Алгоритм нахождения полных множеств взаимно независимых операторов.
Алгоритм.
Пусть W — массив полных множеств ВНО. Максимальное полное множество ВНО обозначим как А, а l — число элементов в нем. Очередное формируемое множество ВНО обозначим как D, d – количество элементов в нем. Номер очередного найденного нулевого элемента в строке обозначим как k. Изначально положим, что стек пуст, W = Ø, А = Ø, l =0, D=Ø, d =0, k=0.
Загрузим очередную i-ю строку в стек, где i = 1,..., п; n — размер матрицы М. Положим D = {i} , d= 1, k=i. Если все строки обработаны, то выполнение алгоритма заканчивается: найдены все полные множества ВНО (W) и определено максимальное (А).
В строке-вершине стека найдем очередной нуль, занимающий позицию j > k. Если нуль найден, то перейдем к выполнению шага 6, иначе выполним следующий шаг.
Если такого нуля нет или все нули найдены, выполняем проверку на полноту найденного множества D. Если в строке-вершине стека все нули соответствуют всем операторам из D, то найденное множество полное. Произведем сохранение Wm = D и перейдем к шагу 7. Если в строке-вершине есть хотя бы один нуль, не соответствующий операторам из D, то найденное множество не является полным. Переходим к следующему шагу.
Исключим из стека строку-вершину (не будем забывать, что, исключая строку, мы уничтожаем и текущие значения k и D, и возвращаемся к их предыдущим значениям). Если после этого стек исчерпан, выполним шаг 2. В противном случае выполним шаг 3.
В текущей вершине стека присвоим k:= j. Складываем логически (поэлементная дизъюнкция) строку, исключая поля k u D из вершины стека, со строкой с номером j — формируем новую вершину стека. В новой вершине стека формируем множество
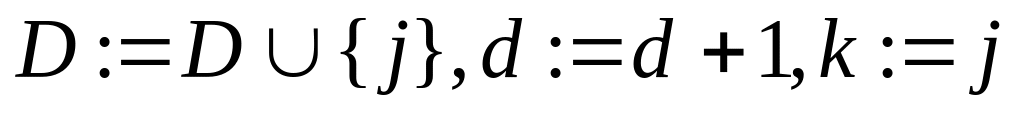 .
Перейдем к
шагу 3.
.
Перейдем к
шагу 3.Сравним значения d и l. Если d > l, то А := D, l := d. Независимо от результата сравнения перейдем к шагу 5.
Конец алгоритма.
28. Алгоритмы построения ранних и поздних сроков окончания выполнения операторов.
Рассмотрим алгоритм,
представляемый информационным графом
(без связей по управлению), не имеющим
контуров. Тогда очевидно, что момент
окончания выполнения любого из операторов
не может быть меньше максимальной из
длин всех путей, заканчивающихся
вершиной, соответствующей этому
оператору. Таким образом, для каждого
оператора алгоритма j
= 1,..., т.
можно найти
ранний срок
![]() окончания его выполнения.
окончания его выполнения.
Если окончание
выполнения алгоритма ограничено временем
![]() ,
то для каждого
оператора можно найти и поздний срок
окончания его выполнения
,
то для каждого
оператора можно найти и поздний срок
окончания его выполнения
![]() (Т).
Здесь ТКР
— максимальная
характеристика пути в графе со
скалярными весами, она определяет
минимальное время, за которое может
быть решена данная задача.
(Т).
Здесь ТКР
— максимальная
характеристика пути в графе со
скалярными весами, она определяет
минимальное время, за которое может
быть решена данная задача.
Окончание выполнения любого оператора позже этого позднего срока приводит к тому, что все последующие за ним операторы не смогут быть выполнены в заданный срок Т, поэтому без задания Т определение поздних сроков не имеет смысла. При Т = Ткр ранние и поздние сроки выполнения операторов, входящие в критический путь, совпадают.
Алгоритм. Нахождение ранних сроков окончания выполнения операторов.
Положим
 где
где
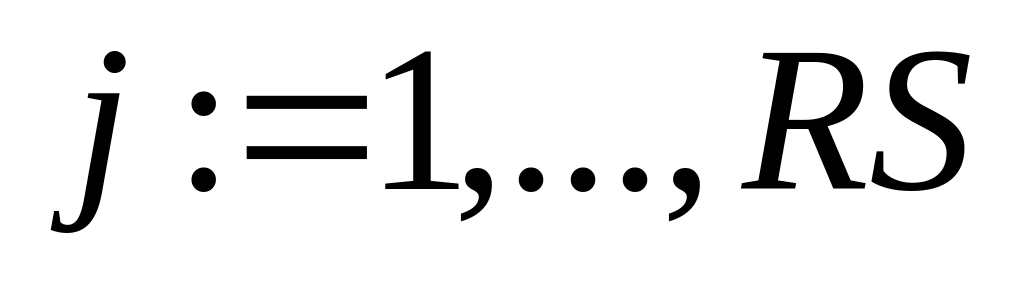 .
.Просмотрим строки матрицы S сверху вниз, выберем первую необработанную строку матрицы и осуществим переход к следующему шагу. Если обработаны все строки, то конец алгоритма,
Пусть выбрана j-я строка, не содержащая единичных элементов. Далее вычислим
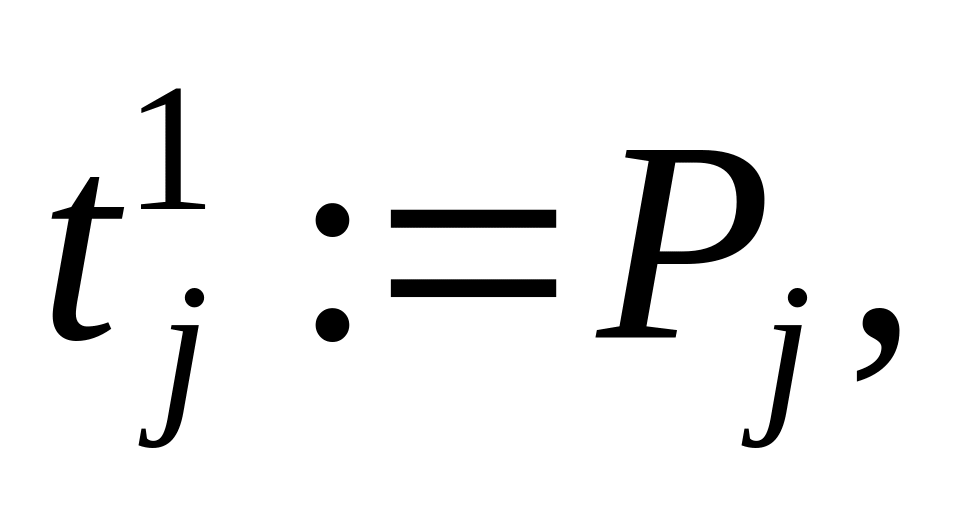 где
где
 — вес j-гo
оператора, затем выполним переход к
шагу 5.
— вес j-гo
оператора, затем выполним переход к
шагу 5.Если j-я строка содержит единичные элементы, то вычислим
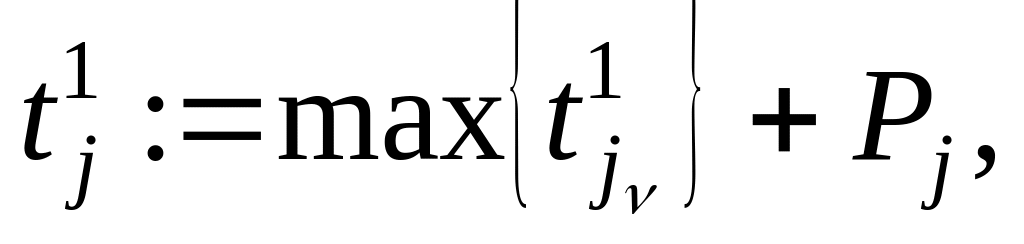 где
где
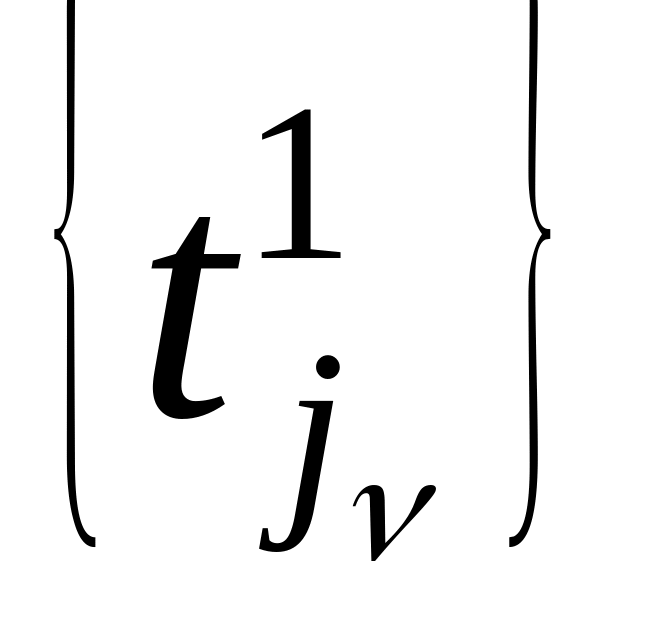 есть множество
времен, которым соответствует единица
в данной строке. Затем выполним переход
на шаг 5. Если во множестве
есть нулевые
элементы, то выполним шаг 6.
есть множество
времен, которым соответствует единица
в данной строке. Затем выполним переход
на шаг 5. Если во множестве
есть нулевые
элементы, то выполним шаг 6.Обработанную j-ю строку исключим из рассмотрения и осуществим переход к шагу 2.
Если найдена строка
 ,
для которой
,
для которой
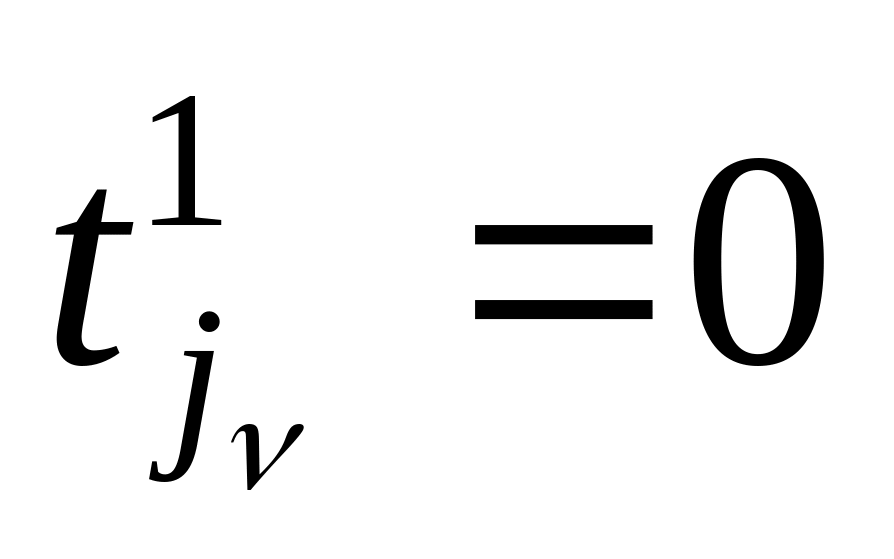 ,
то вычислим строку j=
,
и осуществим
переход к шагу 3.
,
то вычислим строку j=
,
и осуществим
переход к шагу 3.
Конец алгоритма.
Примечание. Пункт 6 используется для нетреугольной матрицы S.
Алгоритм. Получение поздних сроков окончания выполнения операторов.
Положим
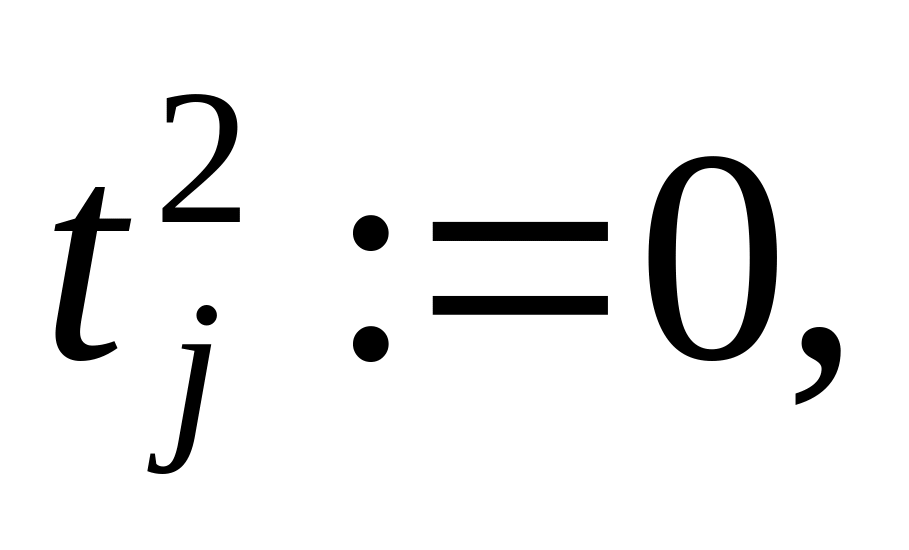 где
..
где
..Просмотрим столбцы матрицы S справа налево, выберем первый необработанный столбец матрицы и произведем переход к следующему шагу. Если обработаны все столбцы, то конец алгоритма.
Пусть j — номер очередного необработанного столбца. Если он не содержит единичных элементов, то вычислим
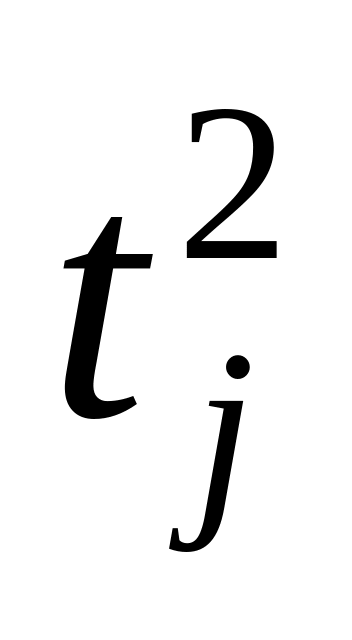 (Т)= Т, где
Т —
время решения задачи, и перейдем к шагу
5.
(Т)= Т, где
Т —
время решения задачи, и перейдем к шагу
5.
Если столбец j содержит единичные элементы, то вычислим
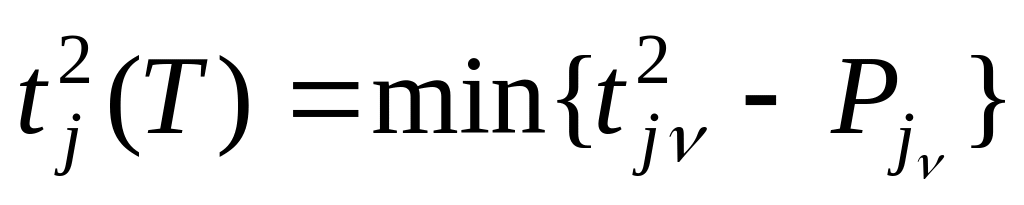 ,т.е.
минимум определим по всем jv
единичным
элементам j-гo
столбца. Если
,т.е.
минимум определим по всем jv
единичным
элементам j-гo
столбца. Если
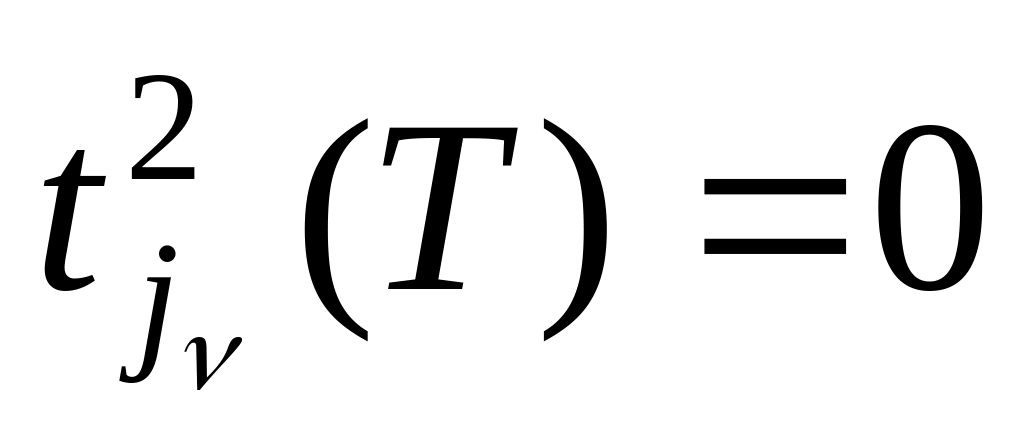 ,
то выполним шаг 6.
,
то выполним шаг 6.Обработанный j-й столбец исключим из рассмотрения, затем выполним шаг 2.
Если найден столбец jv, для которого , то проведем поиск необработанного столбца jv, вычислим j = jv и выполним переход к шагу 3.
Конец алгоритма.
Примечание. Пункт 6 используется для нетреугольной матрицы 3.
Диаграммы выполнения операторов для ранних и поздних сроков — удобный способ наглядного представления многопроцессорной обработки. Всего в диаграмме имеется п строк, соответствующих числу процессоров в системе. Выполнение того или иного оператора отмечается прямоугольниками, имеющими длину, равную весам операторов, и правую границу, соответствующую крайнему сроку окончания выполнения операторов.
29. Определение функции плотности загрузки и минимальной загрузки для вычислительных систем.
Множество входных вершин графа G называется минорантой графа G.
Множество выходных вершин графа G называется мажорантой графа G.
Пусть А есть миноранта, В — мажоранта графа G, a pj – j-го оператора. Тогда множество значений сроков окончания выполнения операторов определяется следующими неравенствами:
![]() ,
если
,
если
![]() (1)
(1)
![]() ,
если существует связь
,
если существует связь
![]() (2)
(2)
![]() ,
если
,
если
![]() (3)
(3)
Множество значений,
определяемых неравенствами (1) — (3),
задает многоугольник МТ
в RS-мерном
пространстве:
![]() .
Тогда
справедливо следующее определение:
.
Тогда
справедливо следующее определение:
Функция
![]() ,
где
,
где
![]() , называется
плотностью
загрузки
ВС в точке для значения
, называется
плотностью
загрузки
ВС в точке для значения
![]() .
.
Значение функции PZ в каждый момент времени формируется операторами множества ВНО, т. е. в каждый момент времени значение функции PZ совпадает с числом одновременно выполняемых операторов.
Функция
![]() называется
загрузкой
отрезка
называется
загрузкой
отрезка
![]() для
для
![]() .
.
Функция Z определяет количество выполненных на этом отрезке операторов (с учетом частично выполненных операторов).
Функция
![]() называется
минимальной
загрузкой
отрезка
для
.
называется
минимальной
загрузкой
отрезка
для
.
Смысл этого
определения заключается в том, что при
решении задачи за время Т при любом
планировании операторов на выполнение
загрузка отрезка
не может быть
меньше вычисленной, согласно
определению величины
![]() .
.
30. Алгоритм определения минимальной загрузки в вычислительной системе на заданном интервале.
Функция
![]() называется загрузкой отрезка
называется загрузкой отрезка
![]() для
для
![]()
![]()
С помощью функции Z определяется загрузка отрезка [a,b], выполняемыми на этом отрезке операторами.
Функция
![]() называется
минимальной загрузкой отрезка
для
называется
минимальной загрузкой отрезка
для
![]()
Смысл этого определения заключается в том, что при любом планировании операторов для выполнения при решении задачи за время Т, загрузка отрезка не может быть меньше вычисленной величины.
Для составления алгоритма вычисления функции введем функцию:
![]()
Алгоритм. Вычисление функции .
С помощью известных алгоритмов вычислим ранние и поздние (T) сроки окончания выполнения операторов.
Положим
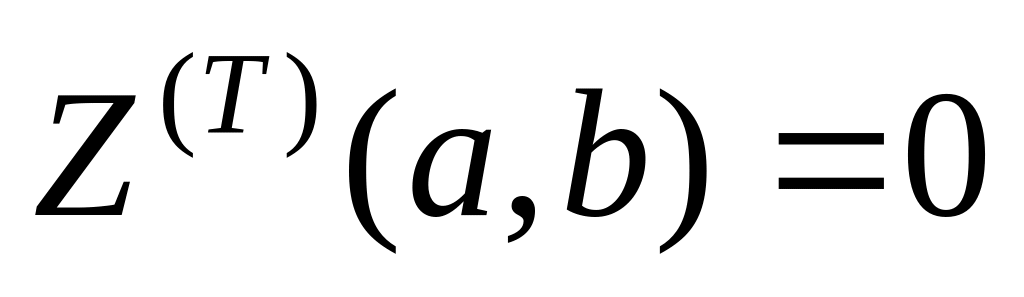 .
.Анализируем последовательность оператора j = 1, ..., RS. Если просмотрены все операторы, то конец алгоритма.
Вычислим
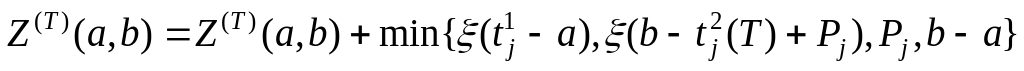 .
.
5.После перебора всех, операторов получим значение . Конец алгоритма.
31. Лемма об оценке максимально необходимого числа процессоров для решения поставленной задачи.
Лемма
(об
оценке сверху требуемого количества
процессоров для решения задачи за время
Т). Минимальное
количество однородных процессоров
N,
способных
выполнить данный алгоритм за время Т
≥ Ткр,
не превышает
![]() ,
где Ci
— число
операторов, которое входит в i-е
полное множество ВНО, полученное для
информационного графа G,
соответствующего исследуемому
алгоритму.
,
где Ci
— число
операторов, которое входит в i-е
полное множество ВНО, полученное для
информационного графа G,
соответствующего исследуемому
алгоритму.
Следствие: При N = Е время решения данного алгоритма Т=Ткр.
Примечание. Получаемое количество процессоров N на основании этой леммы является верхней оценкой требуемого количества процессоров (т. е. для решения данной задачи требуется не более N процессоров).
Теорема (об оценке снизу числа процессов, необходимых для решения задачи за время Т). Для того чтобы N процессоров было достаточно для выполнения заданного алгоритма, представленного информационным графом со скалярными весами вершин за время Т, необходимо, чтобы для отрезка выполнялось соотношение
![]() ,
где
— минимальная загрузка отрезка
,
где
— минимальная загрузка отрезка
![]() .
.
32. Утверждение об оценке минимально необходимого числа процессоров для решения поставленной задачи.
33. Об оценке снизу времени выполнения задачи при заданном количестве процессоров.
34. Уточнение оценки снизу времени выполнения задачи на n процессорах.
Теорема (об оценке снизу времени выполнения задачи при заданном количестве процессоров). Для того чтобы Т было наименьшим временем выполнения алгоритма, представленного информационным графом со скалярными весами вершин, на ВС, состоящей из N процессоров, необходимо, чтобы для отрезка выполнялось соотношение
![]() ,
где
,
где
![]() — минимальная загрузка отрезка
.
— минимальная загрузка отрезка
.
Теорема (об
уточнении оценки снизу времени выполнения
задачи на N
процессорах).
Если Т1
— оценка
снизу времени выполнения алгоритма,
представленного информационным графом
со скалярными весами вершин на ВС,
имеющей N
процессоров,
и если на отрезке
выполняется
соотношение
![]() ,
то наименьшее время Т
реализации
алгоритма удовлетворяет соотношению
,
то наименьшее время Т
реализации
алгоритма удовлетворяет соотношению
![]() .
.
35. Алгоритм определения оценки минимального числа процессоров, необходимых для выполнения алгоритма за время t.
Алгоритм. Оценка минимального числа процессоров, необходимого для выполнения алгоритма за время Т.
1. Положим N:= 0.
2.Последовательно переберем интервалы в порядке
[0,1];
[0,2]; [1,2];
[0,3]; [1,3]; [2,3];
,,,
[0, Т]; [1, Т]; ... [Т–1, Т].
Всего отрезков
![]() .
.
3. Для очередного
интервала
вычислим
![]() , где
определяется
по известному алгоритму.
, где
определяется
по известному алгоритму.
4. Если N1 > N, то N := N1.
5. После обработки всех интервалов получим требуемое N. Конец алгоритма.
36. Алгоритм определения оценки минимального времени t выполнения заданного алгоритма на вычислительной системе, содержащей n процессоров.
Алгоритм. Оценка минимального времени Т выполнения заданного алгоритма на ВС, содержащей N процессоров.
Вычислим
 ,
где
,
где
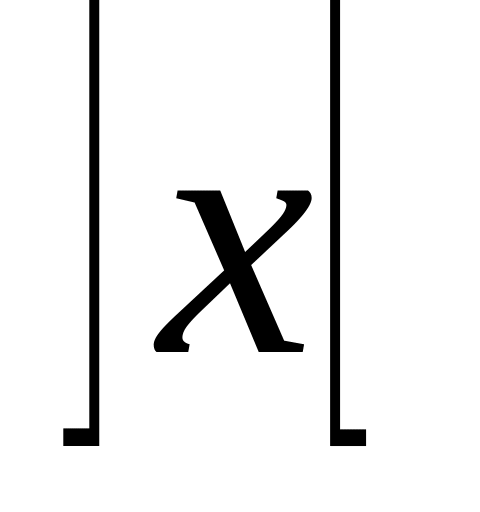 —
ближайшее к х
целое число,
не меньшее х,
pi
— вес i-го
оператора.
—
ближайшее к х
целое число,
не меньшее х,
pi
— вес i-го
оператора.
2. Просмотрим интервалы в порядке
[0,1];
[0,2]; [1,2];
[0,3]; [1,3]; [2,3];
,,,
[0, Т]; [1, Т]; ... [Т–1, Т].
Всего отрезков .
Примечание. При таком выборе последовательности отрезков значение Т можно увеличивать, не пересчитывая при этом ранее вычисленные значения d.
Для очередного интервала вычислим значение
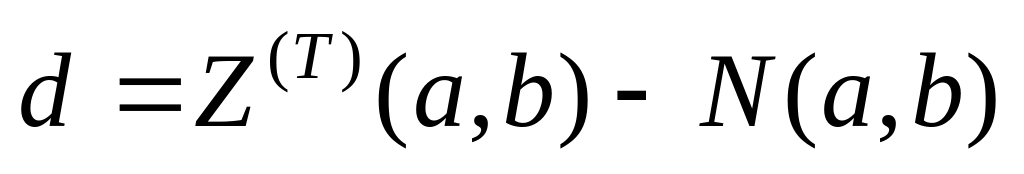 ,
где величина
вычисляется
по известному алгоритму.
,
где величина
вычисляется
по известному алгоритму.Если d > 0, вычислим
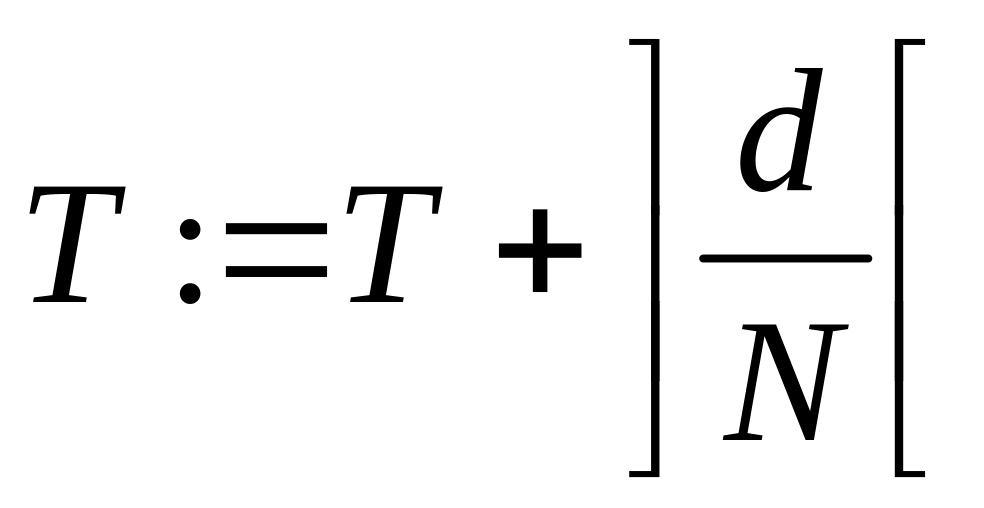 .
.Вычислим
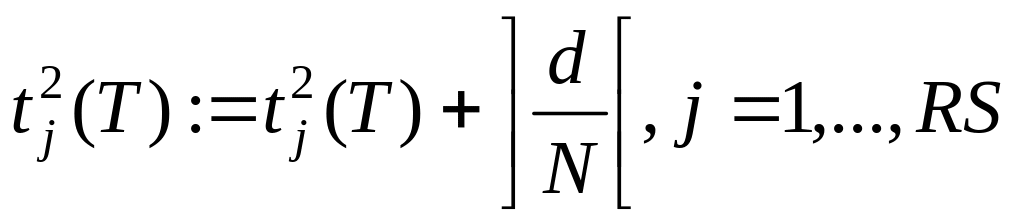 .
.После обработки всех интервалов вычислим значение Т — нижнюю оценку минимального времени выполнения данного алгоритма на данной ВС.
Конец алгоритма.
37. Алгоритм оценки минимально необходимого количества процессоров для задачи, представленной информационно-логическим графом.
Если n – количество
логических операторов в графе, то
![]() -
число образованных информационных
связей.
-
число образованных информационных
связей.
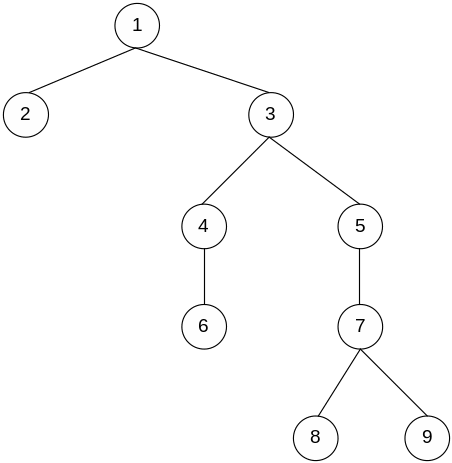
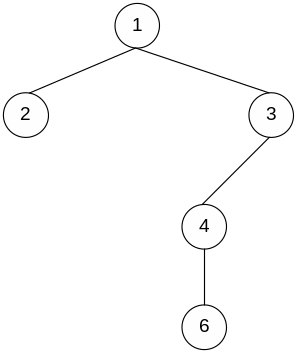
Перенумеруем логические операторы «сверху вниз, слева на право».
Для построения
алгоритма преобразование
информационно-логического графа в
информационный граф, обозначим
![]() или
или
![]() ,
через jTF,
будем считать
при этом
,
через jTF,
будем считать
при этом
Если
![]() ,
то
,
то
![]() ;
;
Если
![]() ,
то
,
то
![]() .
.
Алгоритм
Просматриваем матрицу ST по столбцам слева на право, находим столбец, где имеется значение
 ,
предполагаем, что уровень этого
логического оператора k:=1. Вводим
вспомогательную переменную FLAG:=True,
f:=1.
Если просмотрены все столбцы, то конец
алгоритма.
,
предполагаем, что уровень этого
логического оператора k:=1. Вводим
вспомогательную переменную FLAG:=True,
f:=1.
Если просмотрены все столбцы, то конец
алгоритма.Выбираем связь и преобразуем ее в информационную. Если FLAG:=True, то связь
 временно исключаем из рассмотрения,
вместе со всеми вершинами, доступными
через эту связь. При том полагается,
что исключаемые вершины образуют
неориентированный граф. Иначе
(FLAG:=False)
эта связь больше не рассматривается.
временно исключаем из рассмотрения,
вместе со всеми вершинами, доступными
через эту связь. При том полагается,
что исключаемые вершины образуют
неориентированный граф. Иначе
(FLAG:=False)
эта связь больше не рассматривается.
В столбце j проверяем есть ли значение
 ,
где i – номер строки. Если да, то полагаем
k++, j:=i. Столбец исключаем из рассмотрения
и идем на шаг 2. Иначе формируем
информационный граф.
,
где i – номер строки. Если да, то полагаем
k++, j:=i. Столбец исключаем из рассмотрения
и идем на шаг 2. Иначе формируем
информационный граф.
Если f=k или k=1, то идем на шаг 1. иначе полагаем f:=k
На уровне k полагаем
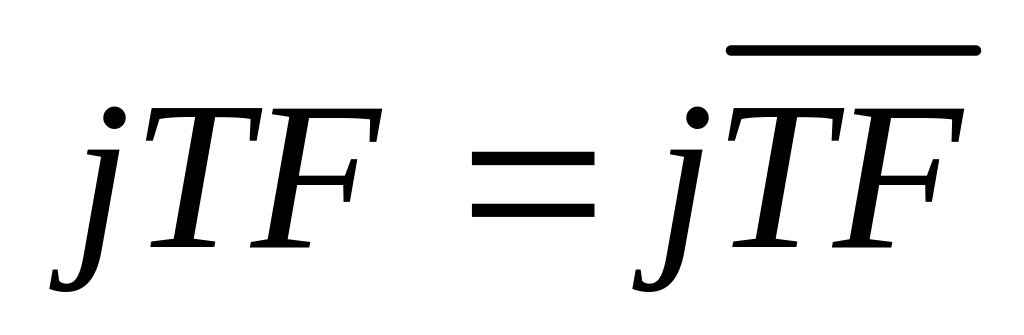 ,
FLAG:=False
и идем на шаг 2.
,
FLAG:=False
и идем на шаг 2.
Алгоритм. (для оценки минимального числа процессоров для ИЛГ)
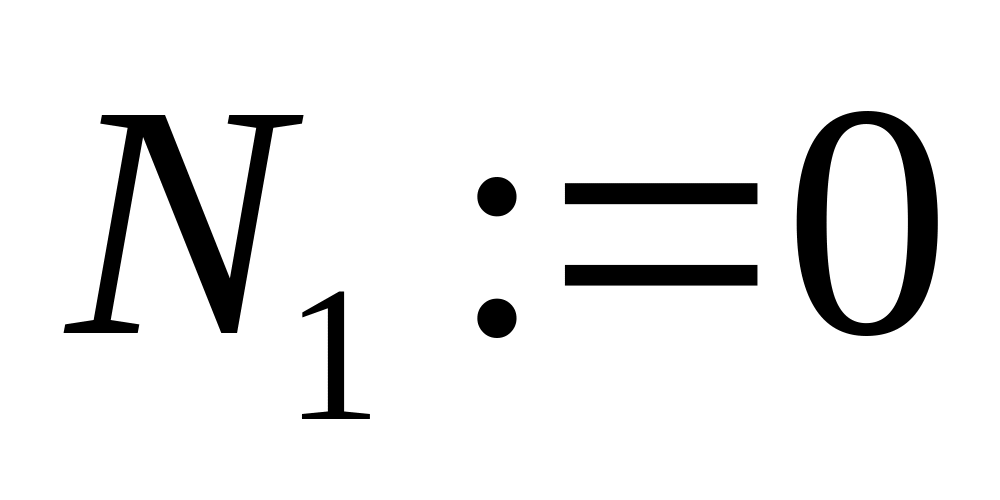
Используя предыдущий алгоритм, находим очередной информационный граф.
Для найденного ИГ, используя алгоритм в вопросе №35, получим нижнюю оценку числа процессоров N.
Если
 ,
то полагаем
,
то полагаем
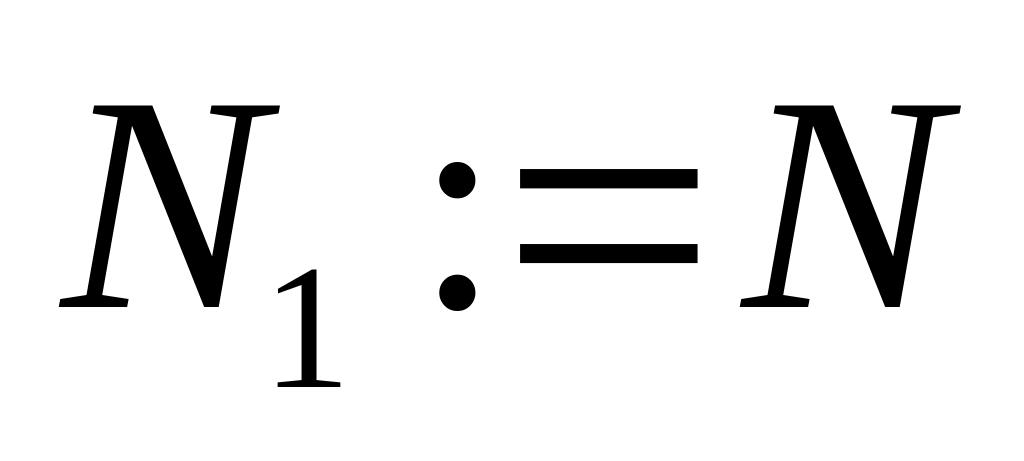
Если обработаны все ИГ, то получается, что значение
 минимальная оценка числа процессоров,
необходимого для решения задачи,
представленной ИЛГ.
минимальная оценка числа процессоров,
необходимого для решения задачи,
представленной ИЛГ.
Конец алгоритма.
38. Алгоритм оценки времени выполнения задачи, представленной данным вычислительных систем графом.
Алгоритм. (Получение нижней оценки времени выполнения задачи представленной данным ИЛГ)
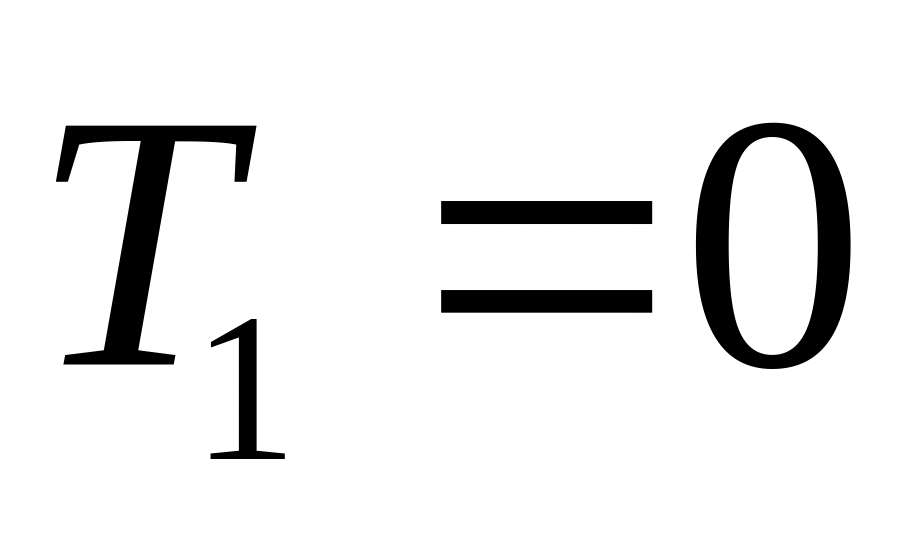
Используя алгоритм из вопроса 37, находим очередной информационный граф.
Используя алгоритм из вопроса 36, для найденного ИГ, вычислим нижнюю оценку времени решения задачи для рассматриваемого ИГ Т.
Если
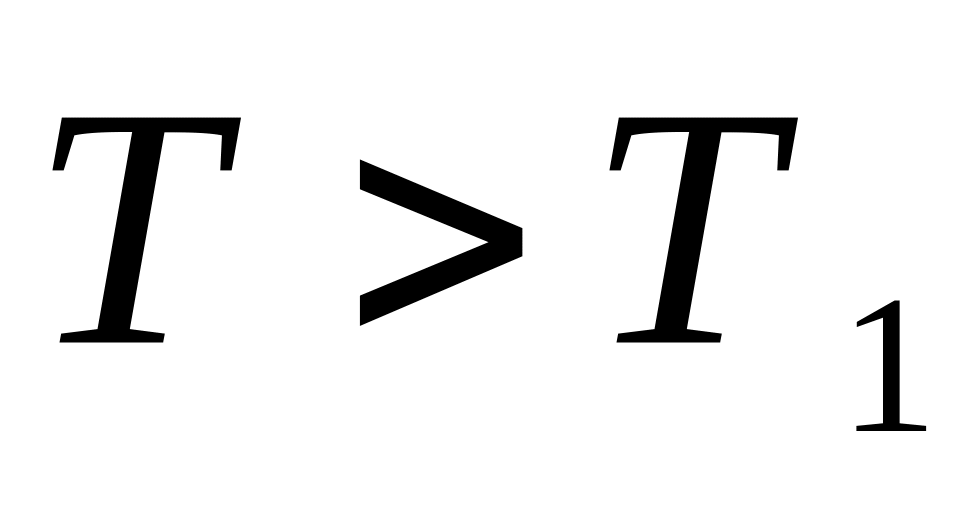 ,
то
,
то
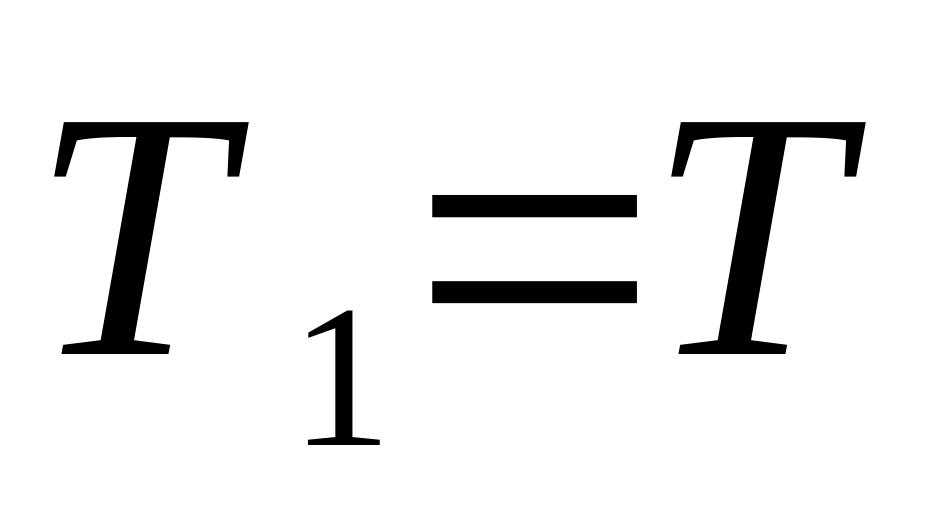
Если обработаны все ИГ, то конец алгоритма.
Конец алгоритма.
39. Архитектурные аспекты при создании операционной системы вычислительных сетей.
Архитектура должна удовлетворять требованиям организации в системе параллельных вычислений во всех режимах. Опыт показывает, что круг задач, допускающих такое представление, достаточно широк. Более того, разработанные методики обеспечивают построение идентичных ветвей таких, что каждая из ветвей состоит их операторов, преобразователей данных, находящихся в памяти, выделенной для этой ветви вычислителя, и относительно редко требуют обращения к памяти других вычислителей. Данное свойство уменьшает остроту вопроса о влиянии структуры ВС в сети межмашинной связи и, в частности, системного устройства, на время обращения к общей или рассредоточенной по вычислителям памяти системы.
В основе организации параллельных вычислений лежит представление вычислителей в виде совокупности совместно протекающих асинхронных и взаимодействующих процессов. Под процессом здесь понимается совокупность последовательных воздействий при реализации в реальном времени некоторого алгоритма на части ресурсов системы. Совместимость процессов означает не только обычную для мультипрограммных систем (в частности, систем разделения времени)одновременность реализации алгоритмически независимых процессов (разделение ресурсов ВС), но и существование связи между отдельными процессами. Эта связь обусловлена тем, что они являются частями одного сложного алгоритма (объединение ресурсов ВС)
40. Опыт применения методики крупноблочного распараллеливания сложных задач.
Сложные задачи допускают построение параллельных алгоритмов, состоящих из идентичных ветвей. Разработка таких алгоритмов, характеризуется простотой, а процесс написания параллельной программы сводиться к написанию последней для одной ветви соответствующего параллельного алгоритма.
При распределении исходных данных между ветвями параллельного алгоритма эффективными являются принципы однородного расщепления массивов информации, при котором обеспечивается равенство объемов составных частей, единообразие при введении избыточности в каждой из них, и взаимнооднозначное соответствие между их номерами и номерами этих ветвей.
Для построения параллельных алгоритмов достаточно использовать 5 схем обмена информацией между ветвями:
дифференциальную;
трансляционную;
трансляционно-циклическую;
конвейерно-параллельную;
коллекторную.
Осуществление обмена по данным схемам в общем случае связывается с транзитным прохождением информации через вычислители, лежащих на пути между взаимодействующими ВС.
Простота реализации обмена по рассмотренным схемам позволяет использовать в основном регулярные однородные структуры ВС и конфигурации подсистем, программно-настраиваемых в пределах ВС в виде линейки, кольца, решетки, гиперкуба и тора.
Для записи параллельных алгоритмов решения сложных задач эффективны версии языков высокого уровня, которые являются расширениями последовательных языков, средствами организации взаимодействия между вычислителями.
Объем системного расширения этих языков составляет несколько % от общего объема транслятора.
Экспериментально установлено, что число программирования на параллельных языках имеет тот же порядок, что и на последовательных. Увеличение трудоемкости укладывается в 10% от трудоемкости последовательного программирования.
Простота схем обмена данных на машинах ведет к простоте записи реализации параллельных программ. Затраты на взаимодействие между программами менее 10% от общего объема программы.
Трансляционно-циклическая, трансляционная конвейерно-параллельная схемы обмена составляют не менее 90% от всех схем, реализуемых в процессе выполнения параллельных программ сложных задач. Время обмена информацией между ветвями параллельной программы, отнесенное к общему времени ее выполнения асимптотически стремиться к нулю с ростом объема исходных данных.
41. Основы функционирования вычислительной системы типа «микрос-т».
Система МИКРОС в виде D2 – графа (степень вершин 4):
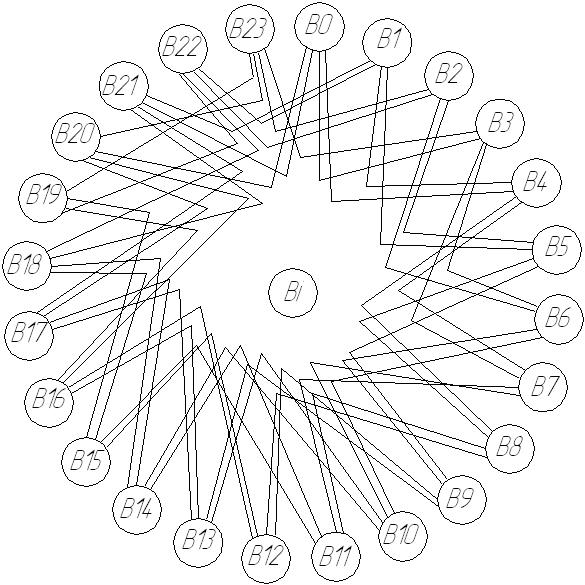 Bi
– вычислитель с транспьютером:
Bi
– вычислитель с транспьютером:
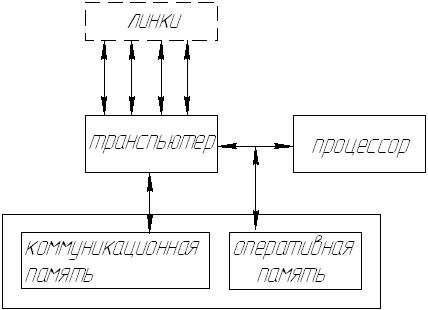
Транспьютер управляет архитектурой этой ВС. В этой структуре может быть распределенный коммутатор.
Транспьютер - сверхбольшая интегральная схема, которая содержит - процессор; - коммуникационные каналы для межпроцессорной связи; - оперативную память; и - кэш небольшого объема. Транспьютер может одновременно принимать, обрабатывать и передавать данные. Транспьютеры позволяют организовать параллельную обработку данных. Транспьютер относят к мультитрейдовой структуре
42. Исследование информационных графов с векторными весами вершин для планирования параллельных вычислений.
Пусть в вычислительной
системе имеется
![]() процессоров, Здесь i задает тип процессора,
а N
задает количество процессоров.
процессоров, Здесь i задает тип процессора,
а N
задает количество процессоров.
Если задача имеет
j операторов, то время выполнения
заданного оператора, на заданном
процессоре будем обозначать как
![]() ,
j=1,
…, m;
i:=1,
…,k.
,
j=1,
…, m;
i:=1,
…,k.
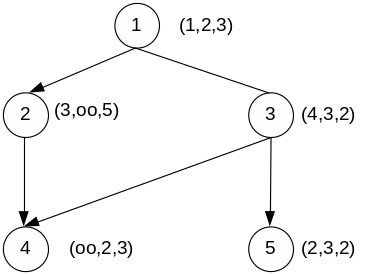
3 типа процессора.
оo – на данном типе процессора задача не может быть решена.
43. Алгоритм нахождения операторов входящих только в одно множество взаимно независимых операторов.
Алгоритм
Матрицу ST' посматриваем сверху вниз по строкам, если просмотрены все строки, то конец алгоритма.
В i-й строке находим множество элементов
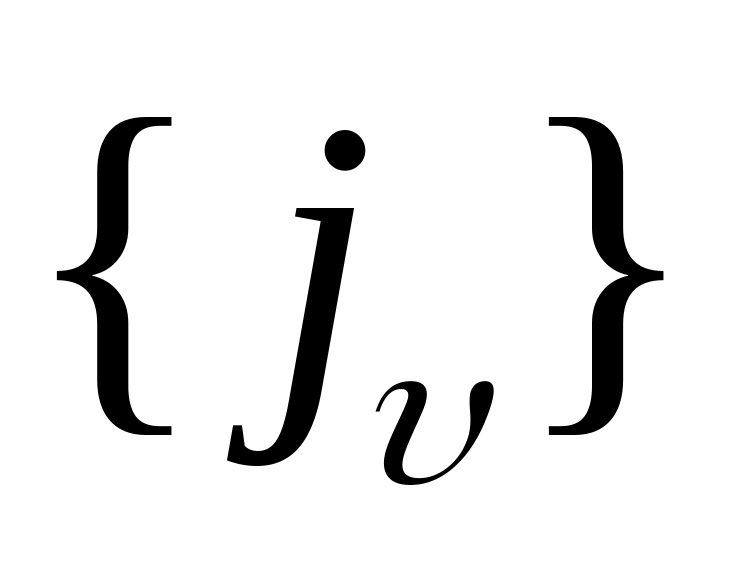 ,
,
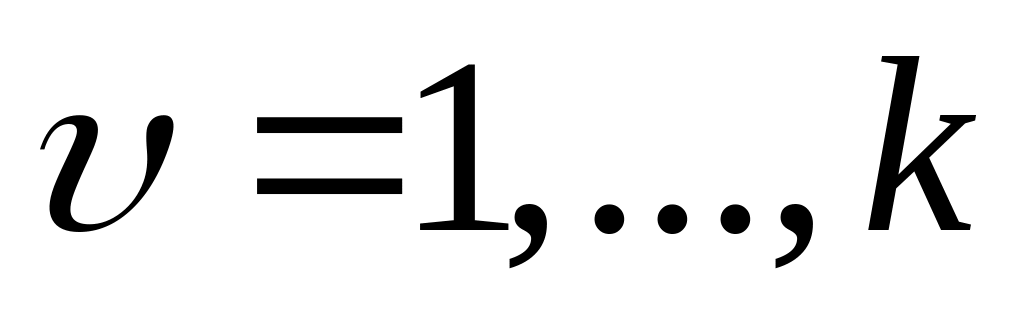 ,
равных 0
,
равных 0Получим дизъюнкцию строк
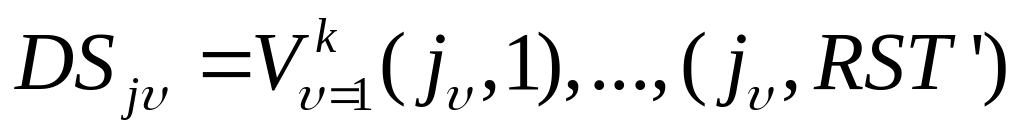
Если i-я строка матрицы ST' совпала со строкой
 ,
то i-й оператор входит в 1 и только в 1
множество ВНО. Само множество ВНО
определяется номерами столбцов, имеющих
нулевые значения в i-й строке.
,
то i-й оператор входит в 1 и только в 1
множество ВНО. Само множество ВНО
определяется номерами столбцов, имеющих
нулевые значения в i-й строке.
46. Определение плотности загрузки для I-го типа процессора и алгоритм ей вычисления.
Определение
20. Плотностью загрузки для i-го
типа процессора, найденной для значений
![]() ,
назовем величину
,
назовем величину
![]() ,
где
,
где
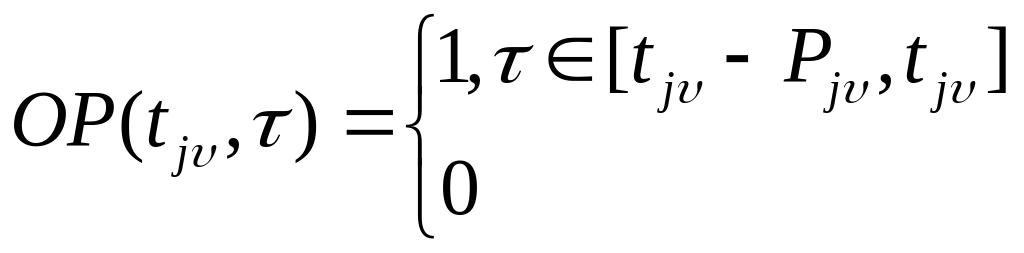
Определение
21. Функцию
![]() назовем загрузкой отрезка [a,b]
входящей в [0, T] для i-го
типа процессора.
назовем загрузкой отрезка [a,b]
входящей в [0, T] для i-го
типа процессора.
![]() назовем минимальной загрузкой отрезка
[a,b] для i-го
типа процессора.
назовем минимальной загрузкой отрезка
[a,b] для i-го
типа процессора.
При
определении
![]() по А12 необходимо учитывать только те
операторы, которые выполняются на i-м
типе процессора.
по А12 необходимо учитывать только те
операторы, которые выполняются на i-м
типе процессора.
Алгоритм 18. (Ранние, поздние сроки)
с помощью А10 и Ф11 определяем
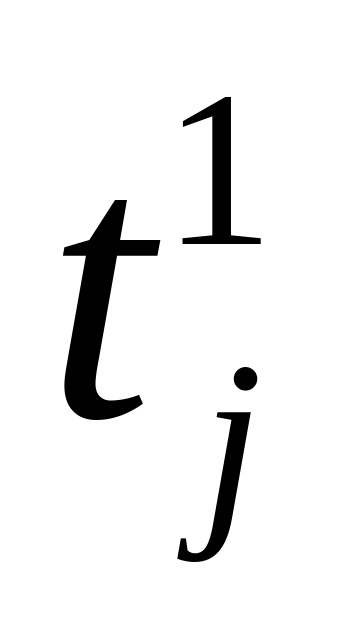 и
и
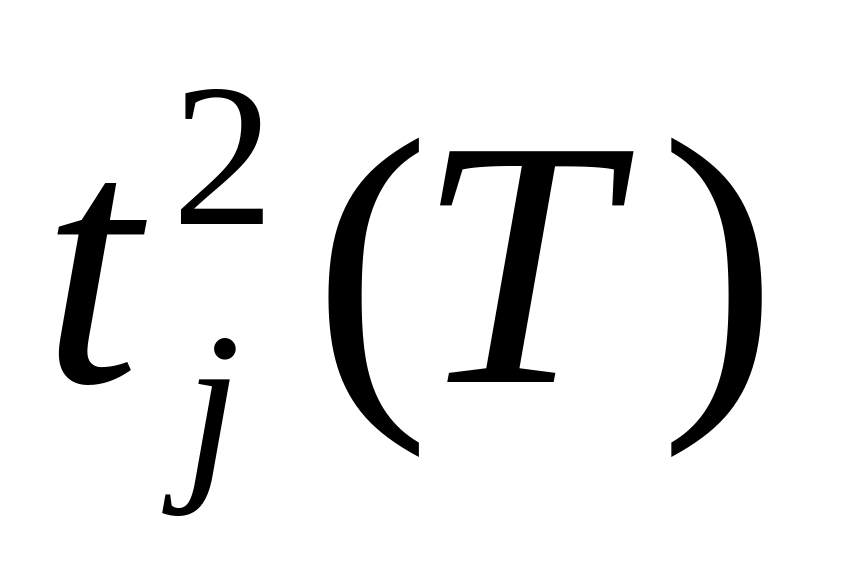
i:=1
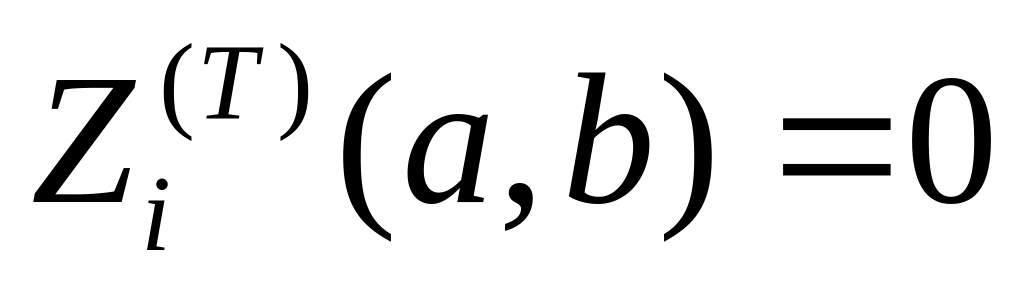
Анализируем последовательность операторов
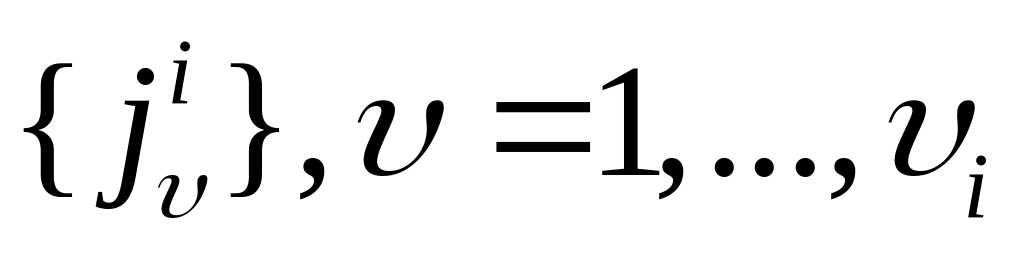
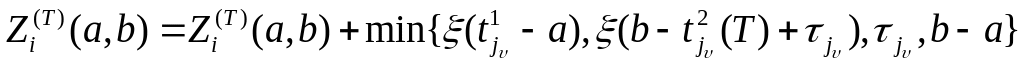
После перебора всех операторов, выполняемых на i-м типе процессора, определяем загрузку i-го типа процессора
Переходим на вычисление загрузки следующего типа процессоров i++. Идем на шаг 3.
После перебора всех значений i получим загрузку всех типов процессоров.
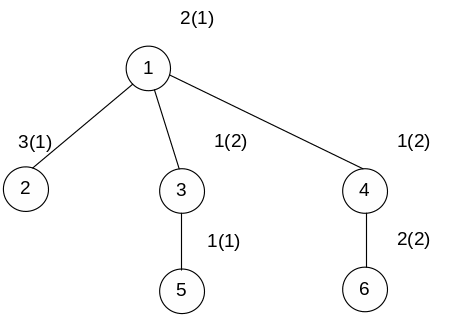
Пример.
 T=8
T=8
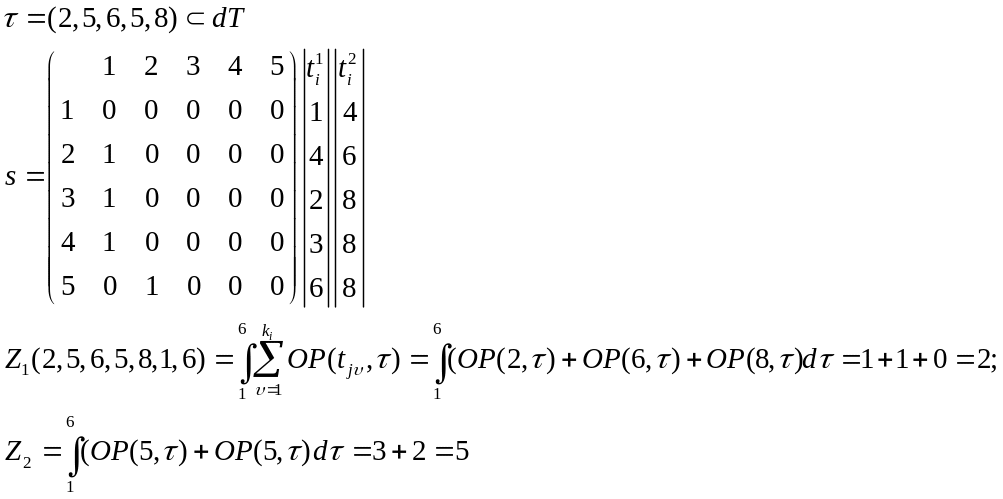
Об
оценке требуемого количества процессоров
![]() ,
или для оценки времени решения задачи,
на наборе процессоров различного типа.
,
или для оценки времени решения задачи,
на наборе процессоров различного типа.
47. УТВЕРЖДЕНИЕ ОБ ОЦЕНКЕ ВРЕМЕНИ ВЫПОЛНЕНИЯ АЛГОРИТМА НА НАБОРЕ ПРОЦЕССОРОВ {NI} I=1..M ИЛИ О ДОСТАТОЧНОСТИ НАБОРА ПРОЦЕССОРОВ {NI} I=1..M ДЛЯ ВЫПОЛНЕНИЯ АЛГОРИТМА ЗА ВРЕМЯ T.
48. УТВЕРЖДЕНИЕ ОБ УТОЧНЕНИИ ОЦЕНКИ ВРЕМЕНИ ВЫПОЛНЕНИЯ АЛГОРИТМА НА НАБОРЕ ПРОЦЕССОРОВ {NI} I=1..M.
Утверждение
1. Пусть каждый оператор данного
алгоритма может быть выполнен процессором
одного и только одного типа из множества
типов i=1,…,k. Тогда для
того, чтобы Т было наименьшим временем
реализации данного алгоритма, состоящего
из множества {
}
процессоров, либо для того, чтобы набор
{
}
был достаточен для выполнения данного
алгоритма за время Т необходимо чтобы
для любого отрезка времени
![]() выполнялось соотношение:
выполнялось соотношение:
![]()
Утверждение 2. Об уточнении оценки времени выполнения алгоритма на наборе процессоров { }.
Пусть
Алгоритм задан информационным графом
со скалярными весами вершин, и каждый
оператор может быть выполнен процессором
одного и только одного типа из множества
типов i=1,…,k. Пусть ВС
состоит из процессоров указанного типа.
Пусть далее
![]() оценка
реализации данного алгоритма на ВС, для
которого на некотором отрезке
оценка
реализации данного алгоритма на ВС, для
которого на некотором отрезке
![]() .
.
Тогда
время выполнения данного алгоритма
![]() .
.
49. АЛГОРИТМ ОЦЕНКИ МИНИМАЛЬНОГО КОЛИЧЕСТВА ПРОЦЕССОРОВ {NI} I=1..M , НЕОБХОДИМОГО ДЛЯ ВЫПОЛНЕНИЯ ЗАДАННОГО АЛГОРИТМА ЗА ВРЕМЯ T.
Алгоритм 19 (об оценке минимального количества процессоров , i=1,…,m необходимой для выполнения заданного алгоритма за время Т)
i=1
=0
Последовательно берутся интервалы , [0,1], [0,2], [1,2],…,[T-1, T]
по А18 вычисляем и затем
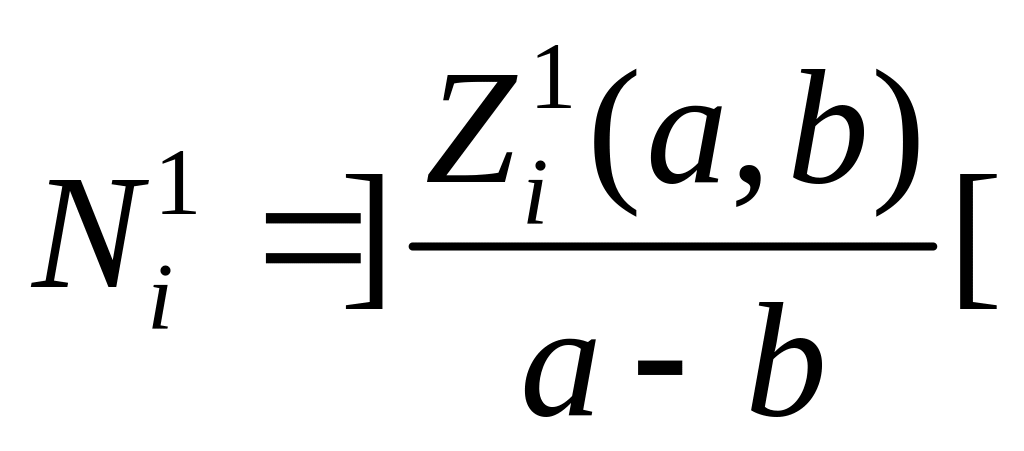
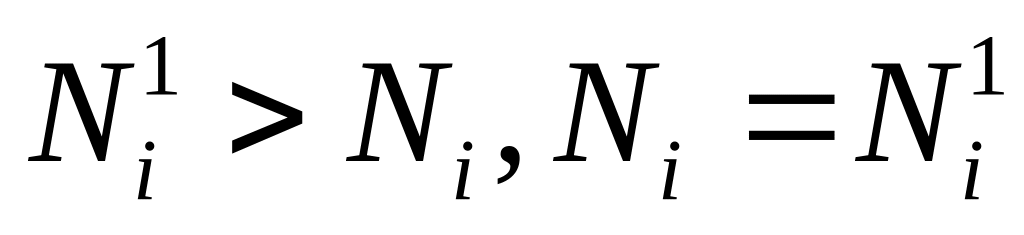
 если i > m
то конец алгоритма, иначе на ш.2
если i > m
то конец алгоритма, иначе на ш.2
Пример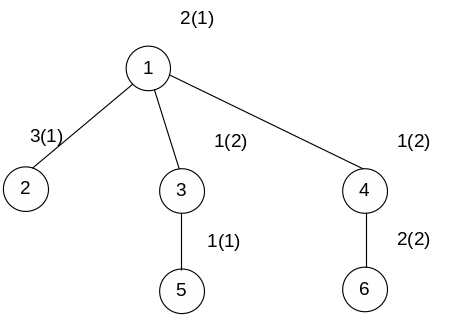 Т=6
Т=6

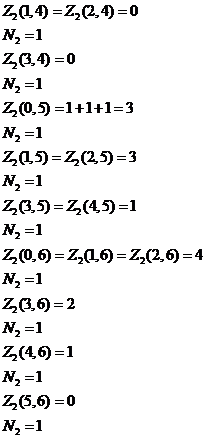
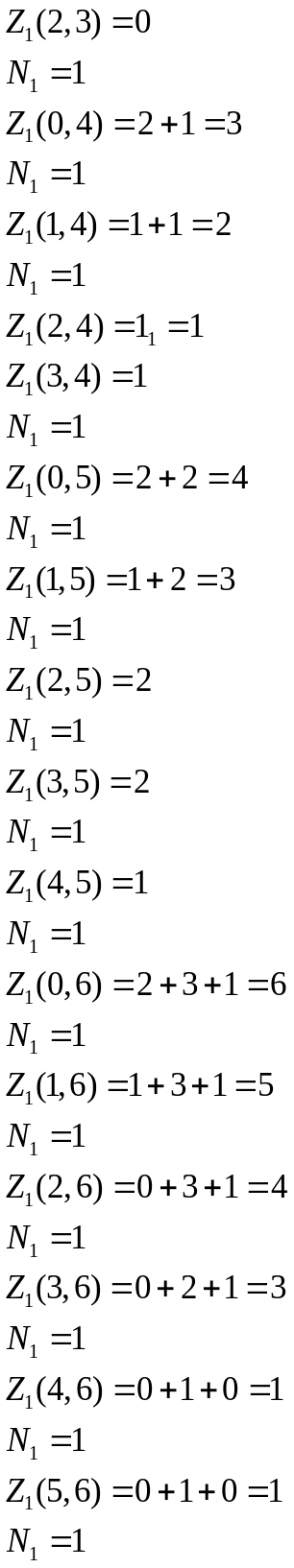
50. АЛГОРИТМ ОЦЕНКИ МИНИМАЛЬНОГО ВРЕМЕНИ ВЫПОЛНЕНИЯ АЛГОРИТМА НА НАБОРЕ ПРОЦЕССОРОВ {NI} I=1..M.
Алгоритм 20 (об оценке минимального времени выполнения алгоритма на наборе процессоров)
{ }, i = 1,…, m
i:=1,
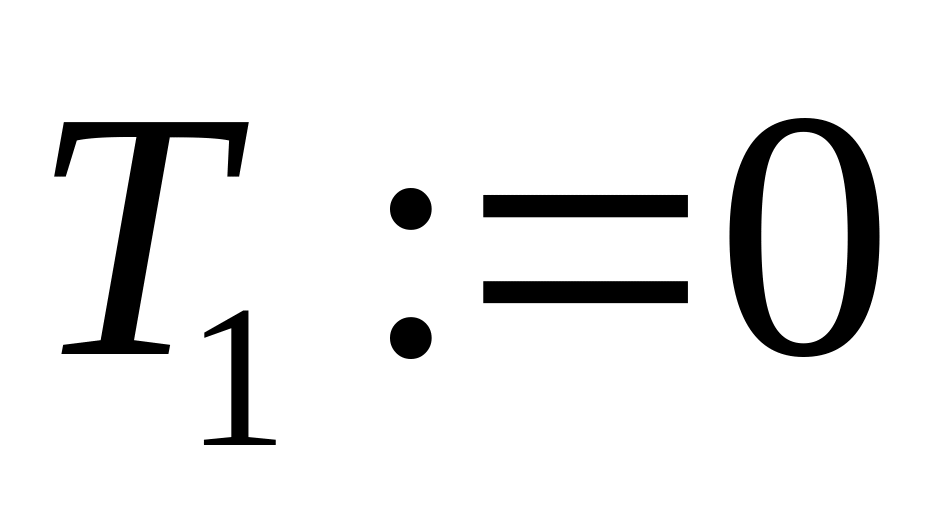
Вычисляем

по А19
[a,b] по А18
![]()
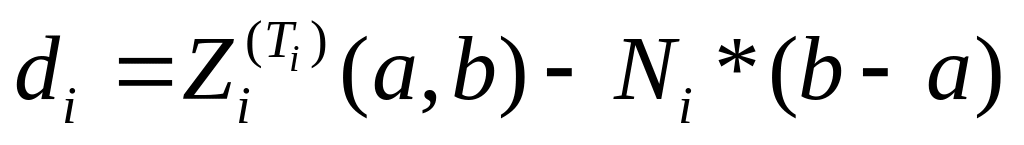
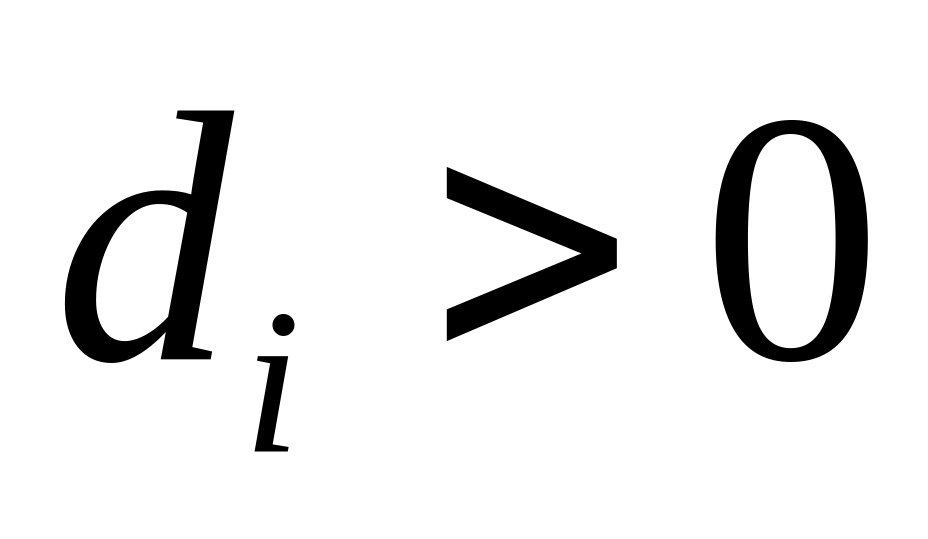 ,
то
,
то
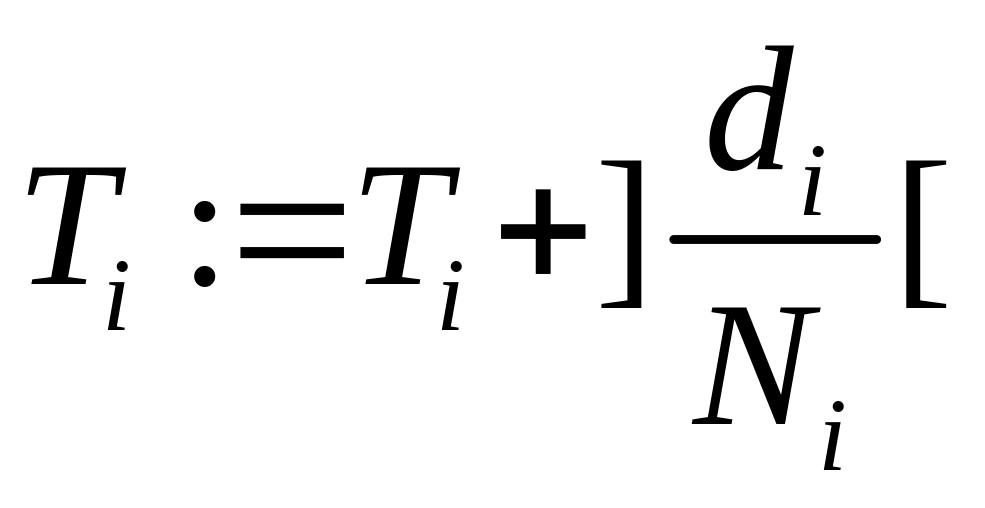
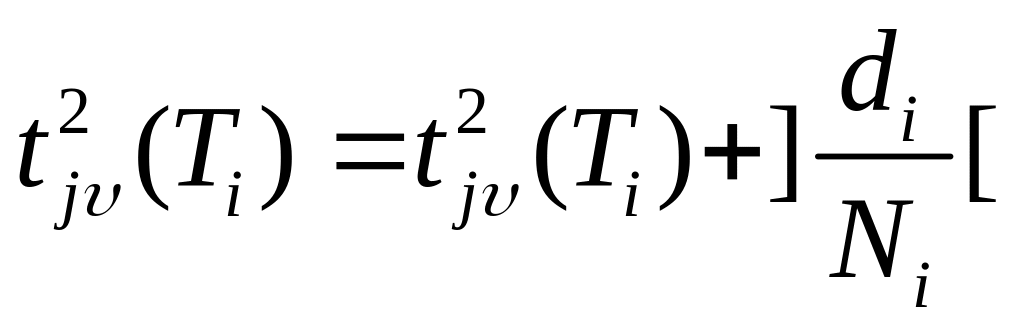 ,
,
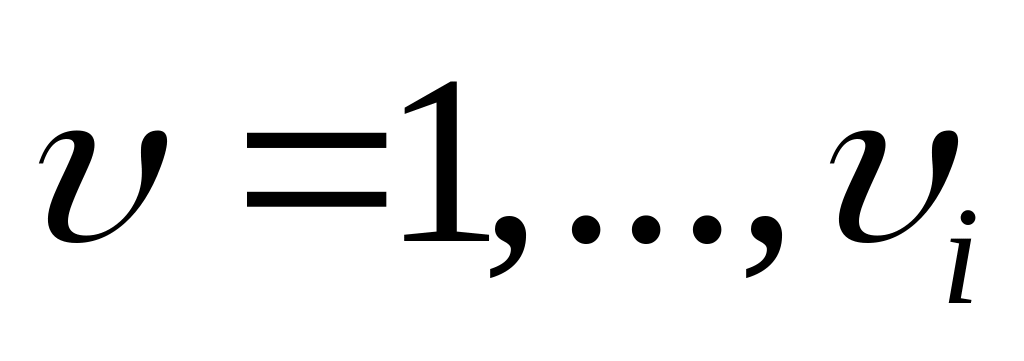
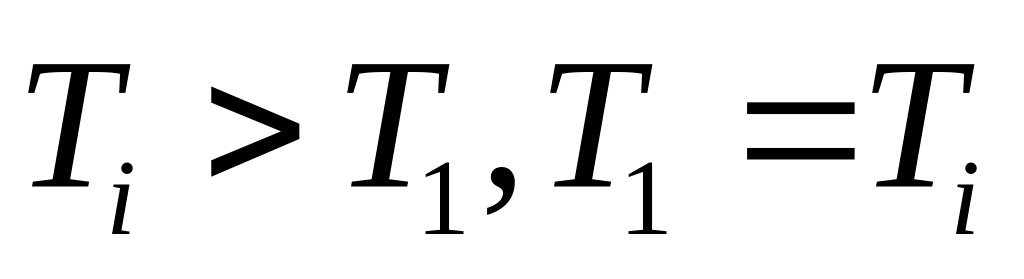
i++
если i>m то конец алгоритма, иначе переходим на ш. 2.
Пример
![]()
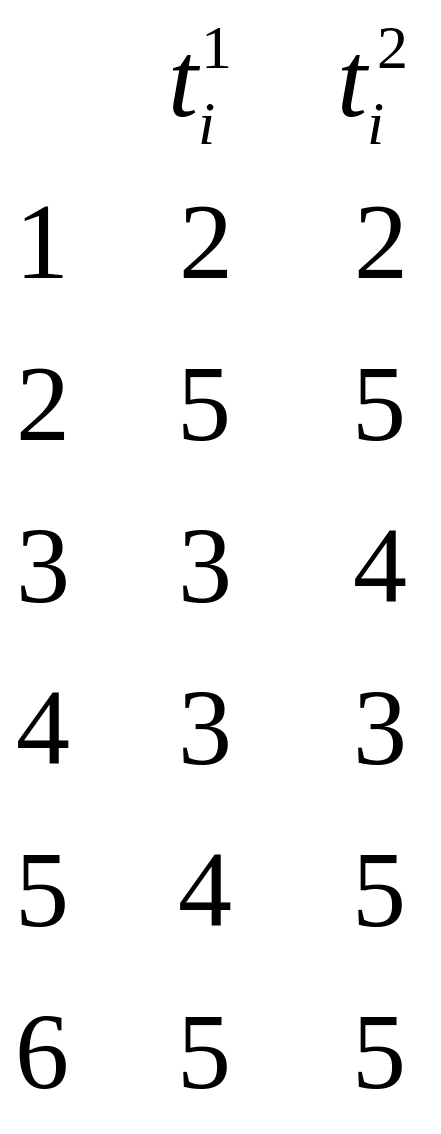
![]()
![]()
51. Коммуникационная среда на основе масштабируемого когерентного интерфейcа sci.
SCI (англ. Scalable Coherent Interface, масштабируемая согласованная взаимосвязь) — компьютерная сеть, используемая для построения кластеров. SCI-кластеры имеют преимущество при решении задач, требующих большого количества пересылок коротких сообщений между узлами, так как в таких задачах время задержки (латентность) играет решающую роль.
SCI принят как стандарт в 1992 г. Он предназначен для достижения высоких скоростей передачи с малым временем задержки и при этом обеспечивает масштабируемую архитектуру, позволяющую строить системы, состоящие из множества блоков. SCI представляет собой комбинацию шины и локальной сети, обеспечивает реализацию когерентности кэш-памяти, размещаемой в узле SCI, посредством механизма распределенных директорий, который улучшает производительность, скрывая затраты на доступ к удаленным данным в модели с распределенной разделяемой памятью. Производительность передачи данных обычно находится в пределах от 200 Мбайт/с до 1000 Мбайт/с на расстояниях десятков метров с использованием электрических кабелей и километров – с использованием оптоволокна. SCI уменьшает время межузловых коммуникаций по сравнению с традиционными схемами передачи данных в сетях путем устранения обращений к программным уровням – операционной системе и библиотекам времени выполнения; коммуникации представляются как часть простой операции загрузки данных процессором (командами load или store). Обычно обращение к данным, физически расположенным в памяти другого вычислительного узла и не находящимся в кэше, приводит к формированию запроса к удаленному узлу для получения необходимых данных, которые в течение нескольких микросекунд доставляются в локальный кэш, и выполнение программы продолжается. Прежний подход требовал формирования пакетов на программном уровне с последующей передачей их аппаратному обеспечению. Точно так же происходил и прием, в результате чего задержки были в сотни раз больше, чем у SCI.
Еще одно преимущество SCI – использование простых протоколов типа RISC, которые обеспечивают большую пропускную способность. Узлы с адаптерами SCI могут использовать для соединения коммутаторы или же соединяться в кольцо. Обычно каждый узел оказывается включенным в два кольца.
S CI
– дуплексный, UART-типа. Это асинхронная
система со стандартным форматом «без
возврата к нулю» (NRZ) для переданного
или полученного бита. Длина переданного
слова 10 - 11 бит (1 старт-бит, 8 - 9 информационных
разрядов, 1 стоп-бит). SCI состоит из трех
модулей: приемник, передатчик и контроллер
скорости пересылки данных в бодах.
CI
– дуплексный, UART-типа. Это асинхронная
система со стандартным форматом «без
возврата к нулю» (NRZ) для переданного
или полученного бита. Длина переданного
слова 10 - 11 бит (1 старт-бит, 8 - 9 информационных
разрядов, 1 стоп-бит). SCI состоит из трех
модулей: приемник, передатчик и контроллер
скорости пересылки данных в бодах.
Характеристики:
Производитель: компания Dolphin
Пропускная способность: физическая скорость передачи — 667 Мб/сек, в зависимости от используемых аппаратных платформ пропускная способность на уровне MPI — от 200 до 325 Мб/сек.
Время задержки: этот тип коммуникационной среды отличается рекордно низким временем задержки: 2—3 мкс — аппаратное и около 4 мкс — на уровне MPI.
Топология: кольцо, двух- или трехмерный тор, а также коммутируемые кольца. В связи с такой топологией, при увеличении размеров тора происходит насыщение аппаратной пропускной способности, поэтому нецелесообразно строить кластеры с размером тора больше 6—8 по каждому измерению. Тороидальная топология не требует применения коммутаторов.
52. Коммуникационная среда на основе технологии myrinet.
Myrinet — широко применяемый для построения кластеров тип коммуникационной среды. Ранее до 28 % (июнь 2005) кластерных установок из списка Top500 самых мощных компьютеров мира были построены с применением Myrinet. Теперь этот показатель упал до 2 % (2009 год).
Технология Myrinet основана на использовании многопортовых коммутаторов при ограниченных несколькими метрами длинах связей узлов с портами коммутатора. Узлы в Myrinet соединяются друг с другом через коммутатор (до 128 портов). Максимальная длина линий связи варьируется в зависимости от конкретной реализации.
Как коммутируемая сеть, аналогичная по структуре сегментам Ethernet, соединенным с помощью коммутаторов, Myrinet может одновременно передавать несколько пакетов, каждый из которых идет со скоростью, близкой к 2 Гбит/с. В отличие от некоммутированных Ethernet и FDDI сетей, которые разделяют общую среду передачи, совокупная пропускная способность сети Myrinet возрастает с увеличением количества машин. На сегодня Myrinet чаще всего используют как локальную сеть (LAN) сравнительно небольшого размера, связывая вместе компьютеры внутри комнаты или здания. Из-за своей высокой скорости, малого времени задержки, прямой коммутации и умеренной стоимости Myrinet часто используется для объединения компьютеров в кластеры. Myrinet также используется как системная сеть (System Area Network, SAN), которая может объединять компьютеры в кластер внутри стойки с той же производительностью, но с более низкой стоимостью, чем Myrinet LAN. Пакеты Myrinet могут иметь любую длину. Таким образом, они могут включать в себя другие типы пакетов, в том числе IP-пакеты. Объединение вычислительных узлов с адаптерами Myrinet в сеть происходит с помощью коммутаторов, которые имеют сейчас 4, 8, 12 или 16 портов. В коммутаторах используется передача пакетов путем установления соединения на время передачи, для маршрутизации сообщений применяется алгоритм прокладки пути (wormhole, "червоточина"). Коммутаторы, как и сетевые адаптеры, построены на специализированных микропроцессорах LANai компании Myricom.
Характеристики:
Производитель: компания Myricom.
Пропускная способность: 250 Мб/сек, 1250 Мб/сек (Myri-10G).
Время задержки — около 10 мкс.
Топология: коммутируемая, элементом коммутации является матрица 8х8. Коммутаторы на её основе поддерживают до 128 портов.
53. Краткая характеристика коммуникационной среды qsnet II.
QsNet — коммуникационная среда от компании Quadrics, обеспечивающая задержки на уровне SCI и пропускную способность до 900 мегабайт/сек (QsNet II). Ввиду высокой стоимости оборудования QsNet, как правило, применяется для построения особо крупных кластеров терафлопного диапазона.
QsNet II - это наиболее производительная коммуникационная среда, обеспечивающая пропускную способность до 910 Мб/сек и рекордно низкое время задержки при передаче программных пакетов от 1.5 до 2.5 микросекунд в зависимости от процессора. Архитектура QsNet II поддерживает несколько тысяч вычислительных узлов, обеспечивая непревзойденную масштабируемость приложений.
Пиковая пропускная способность каналов - 1064 MBytes/sec (достигается 900 MBytes/sec в одном направлении, и 1800 MBytes/sec в режиме Multi-rail). Латентность в рамках MPI - порядка 1,5 мксек. Максимальный размер системы - более 4000 узлов.
54. Алгоритм распределения нитей граф-схемы алгоритма по узлам вычислительной сети.
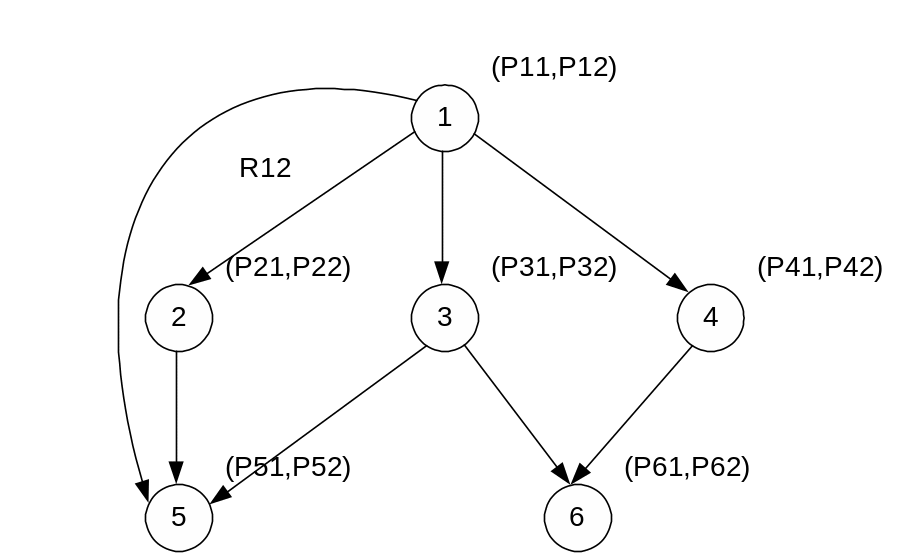
![]() -
объемы передаваемой информации
-
объемы передаваемой информации
l – пропускная способность магистрали.
![]()
Пусть i-я вершина связана с несколькими вершинами в графе, множество вершин назовем разверткой вершины i (J).

Условимся, что в случае такой развертке сигнал в линиях передается одновременно.
Множество J вершин, связанных с рассматриваемой – назовем сверткой вершин.
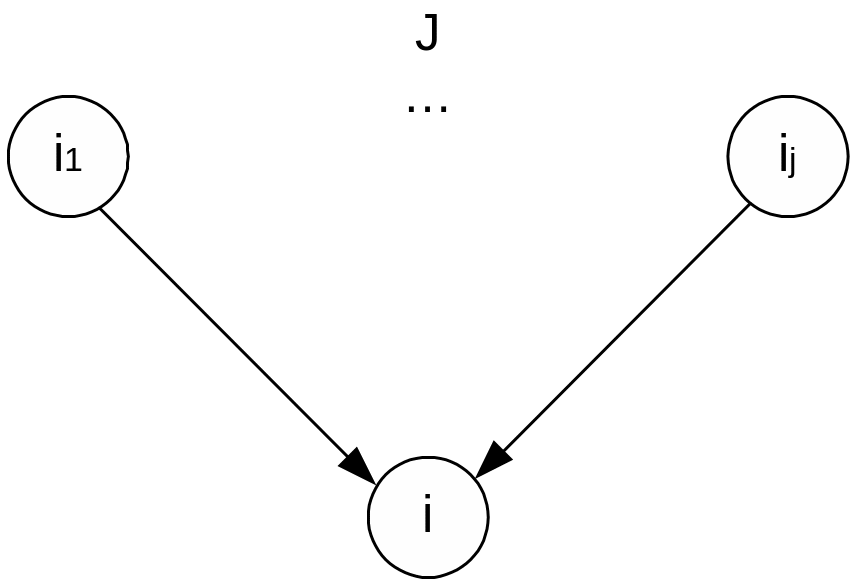
Будем также полагать здесь, что приход любой связи начинал выполнение модуля. Кроме того, мы между связями можем установить логические функции. Такая трактовка свертки позволяет строить ВС, которая не решает какие-то задачи, а выполняет сервисные функции.
Нитью сети, решающей задачу, будем называть цепь, в которой вес входящей или выходящей дуги может быть прибавлен к весу вершины.
Алгоритм 20 (Построение нитей в сети G представляющей решаемую задачу)
В графе G выберем множество начальных вершин
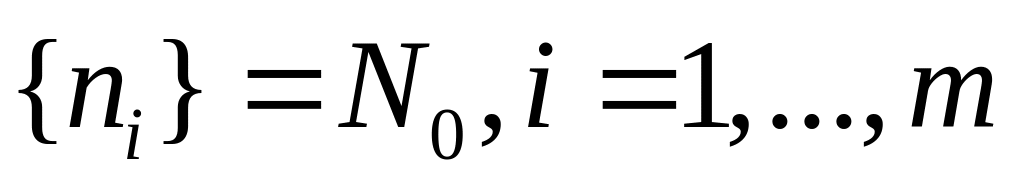 (В матрице S начальным вершинам
соответствуют нулевые строки).
(В матрице S начальным вершинам
соответствуют нулевые строки).
I:=1 – параметр определяющий
текущий номе в множестве
![]()
V:= 1 – номер массива перебора операторов
k:=1 – номер очередной создаваемой нити.
![]() -
множество связей нити с другими нитями
-
множество связей нити с другими нитями
f:=0 – номер очередного разрезания графа G
- множество продолжения нитей
Возьмем вершину
Вычислим обобщенный вес вершины
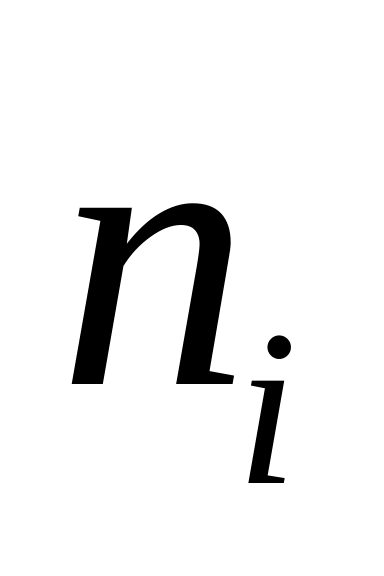 ,
,
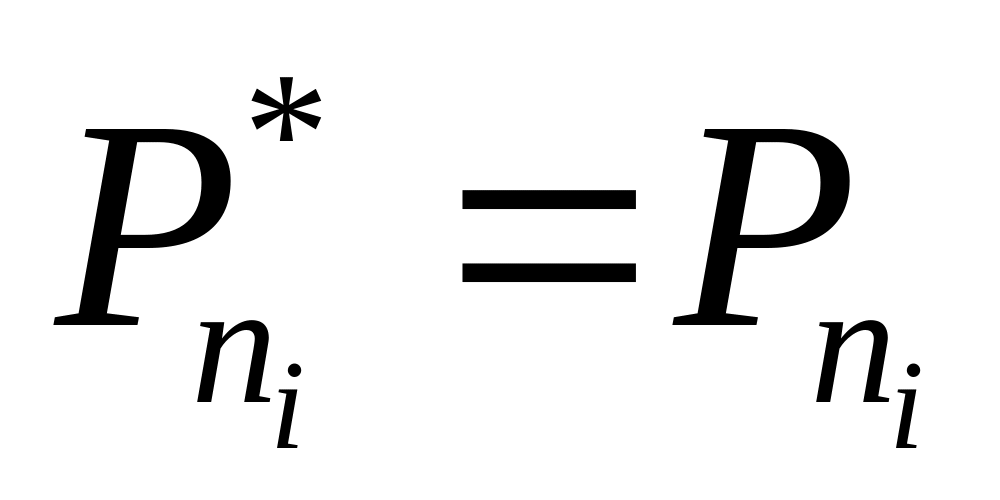 если
вес
вершины не модифицировался
если
вес
вершины не модифицировался
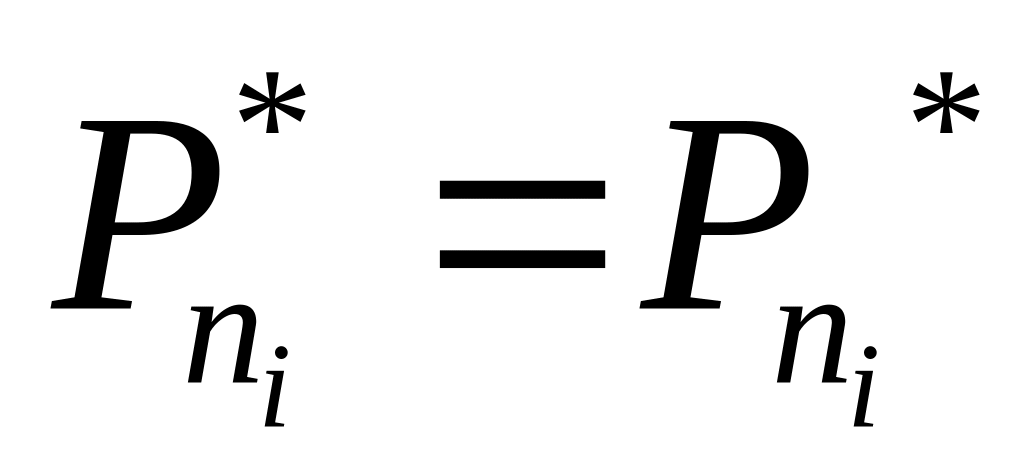 . Иначе: шаг 4
. Иначе: шаг 4Если из вершины не выходит связь, то переходим на шаг 9. Иначе: шаг 5
Если из выходит 1 связь в j-ю вершину, тоесть в матрице S в строке содержится единица в i-й строке.
Если j-я вершина не модифицировалась . Иначе
Обобщенный вес вершины определяем как в шаге 3. Переходим к шагу 10. Иначе к следующему шагу.
Если из вершины
выходит несколько связей (Развертка),
то среди множества дуг J, исходящих из
вершины
ищем
максимум
![]() (1)
(1)
Если условию (1) удовлетворяет несколько вершин, то выбираем первую. в множестве
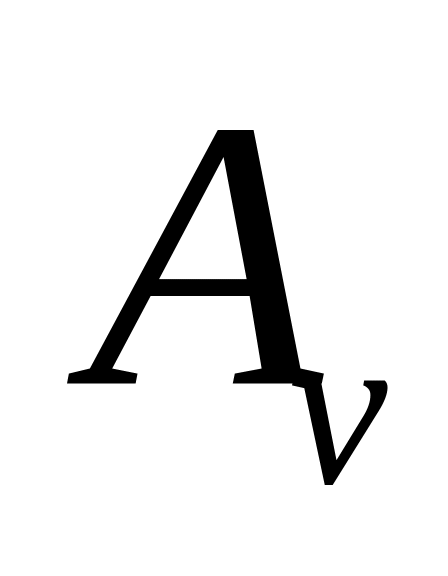 фиксируется последовательно номера
операторов, которые удовлетворяют
условию (1) (для 4-х вершин
фиксируется последовательно номера
операторов, которые удовлетворяют
условию (1) (для 4-х вершин
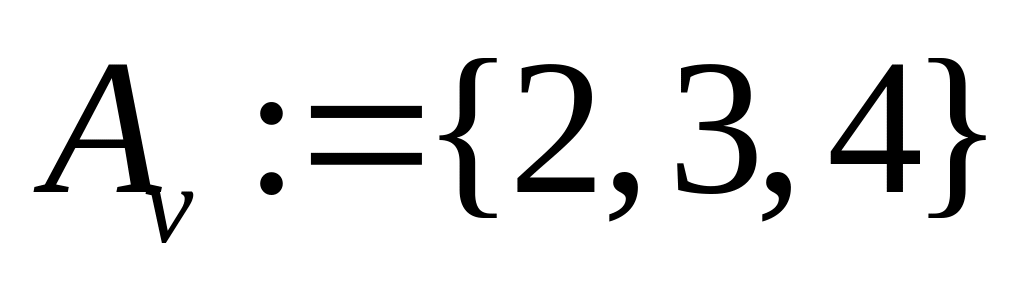 ).
- выходной параметр алгоритма.
).
- выходной параметр алгоритма.
Для вершины
![]() вычисляется вес. Если вершина не
модифицировалась
вычисляется вес. Если вершина не
модифицировалась
Весами вершины множества J исключая вершину вычисляется как
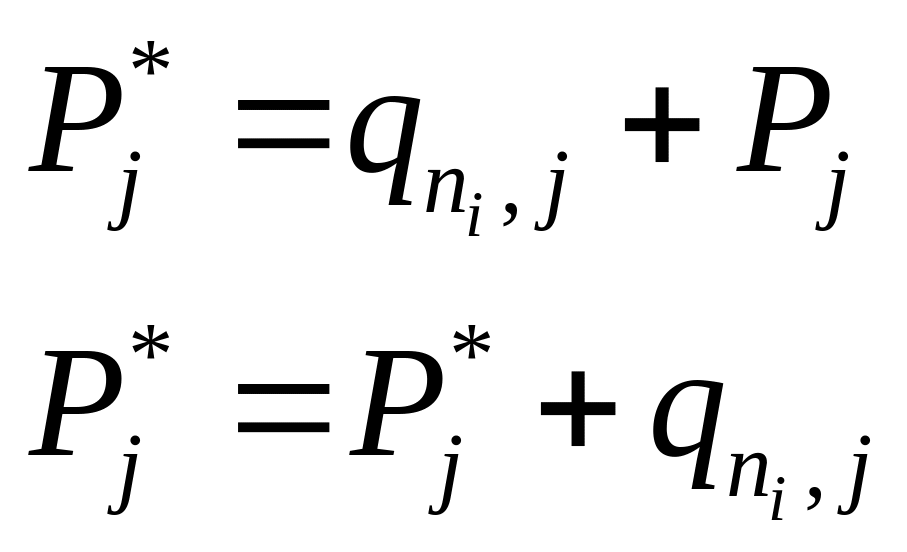
Где
![]() - Обобщенный вес вершины считаем, как
на шаге 3. Переходим на шаг 11.
- Обобщенный вес вершины считаем, как
на шаге 3. Переходим на шаг 11.
Если из вершины - не выходит несколько связей, то идем на следующий шаг.
Если вершина - Входит в сверку J, то обобщенный вес вершины , связанной с вершиной вычисляется как
 .
Веса остальных вершин (исключая вершину
)
вычисляются как
.
Веса остальных вершин (исключая вершину
)
вычисляются как
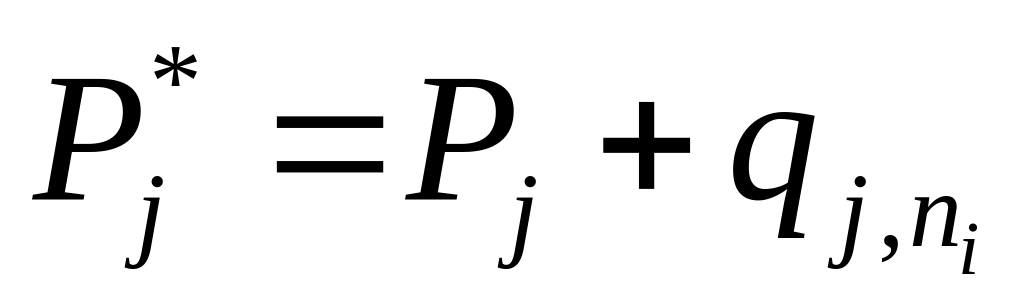 ,
,
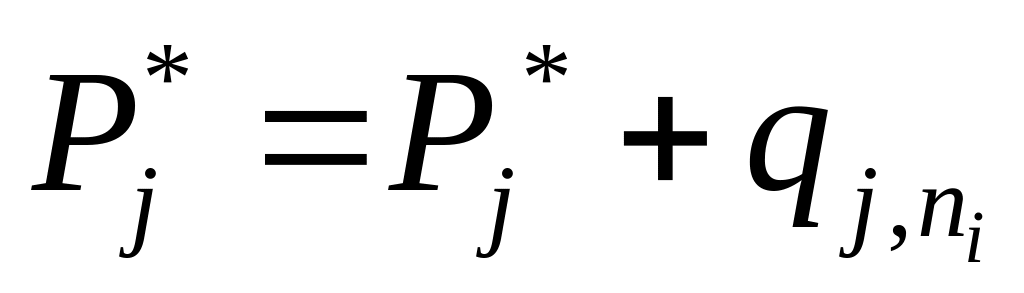 если
вершина не модифицировалась. Обобщенный
вес
как на шаге 3.
если
вершина не модифицировалась. Обобщенный
вес
как на шаге 3.Вершина включается в
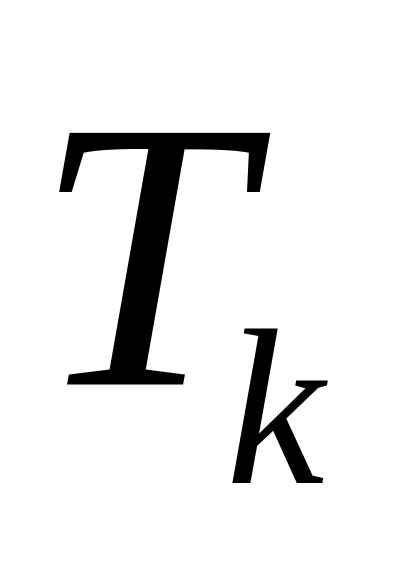 -ю
нить и исключается из рассмотрения, а
-я
нить, включается в множество NT.
-ю
нить и исключается из рассмотрения, а
-я
нить, включается в множество NT.Вычислим
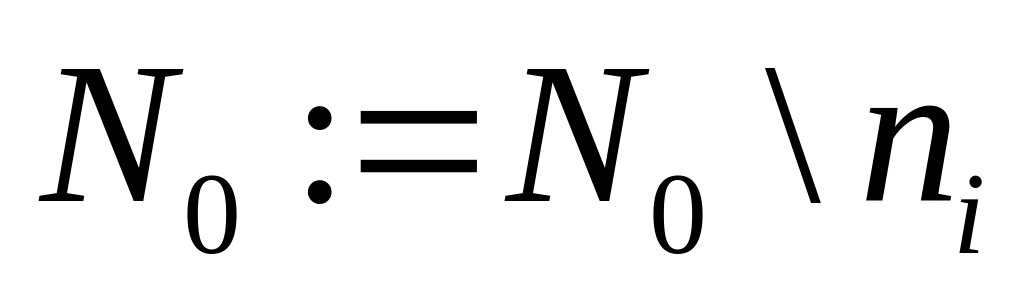
k++
![]()
Если
![]()
![]() ,
то f++, шаг 13. Иначе i++, шаг 2.
,
то f++, шаг 13. Иначе i++, шаг 2.
Вершина , оформляется, как элемент
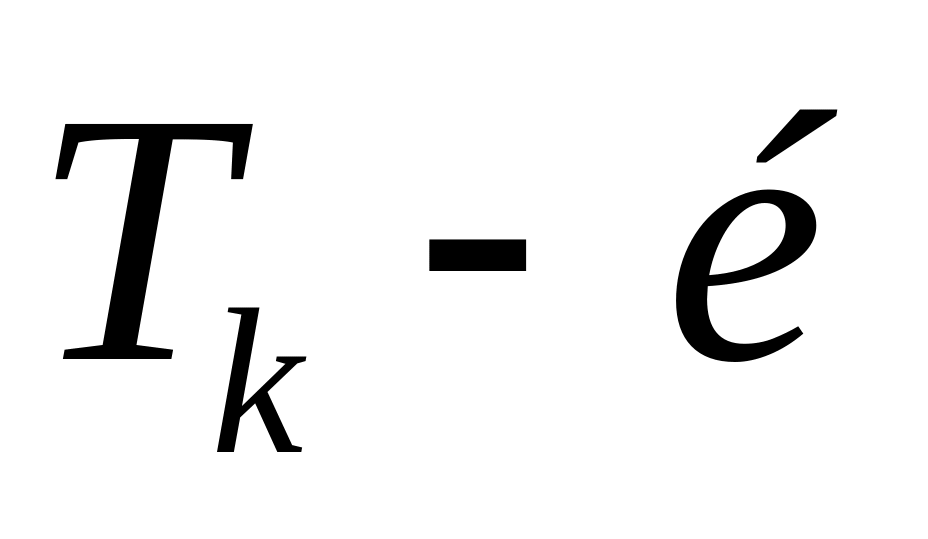 нити и исключается из рассмотрения.
Вершина
,
включается в
,
дуги (
нити и исключается из рассмотрения.
Вершина
,
включается в
,
дуги ( )
исключаются из графа G
или его компонента. Составляется таблица
связей
)
исключаются из графа G
или его компонента. Составляется таблица
связей
 в виде объединений множеств
в виде объединений множеств
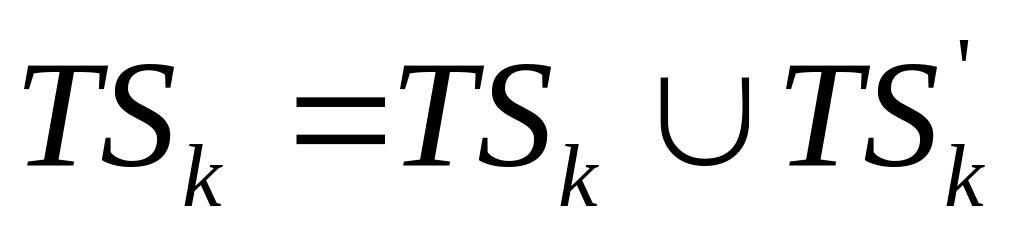 ,
где
,
где
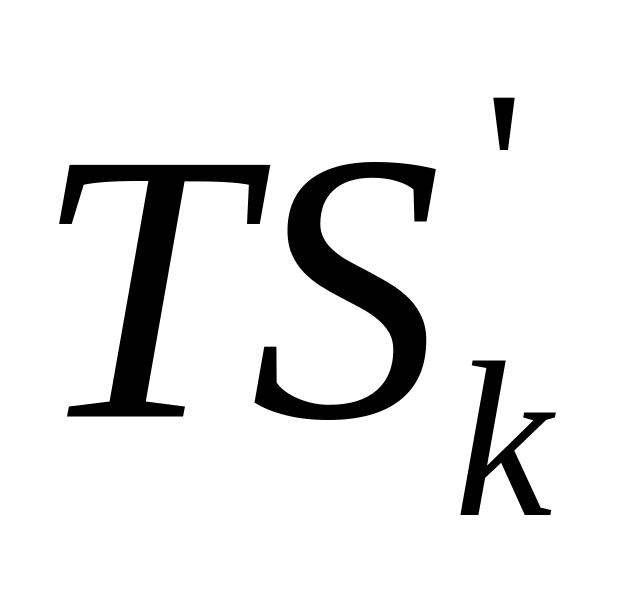 - включает номера операторов множества
J, исключая
.
- включает номера операторов множества
J, исключая
.Вершина оформляется, как элемент нити и исключается из рассмотрения. Вершина , включается в , дуги (
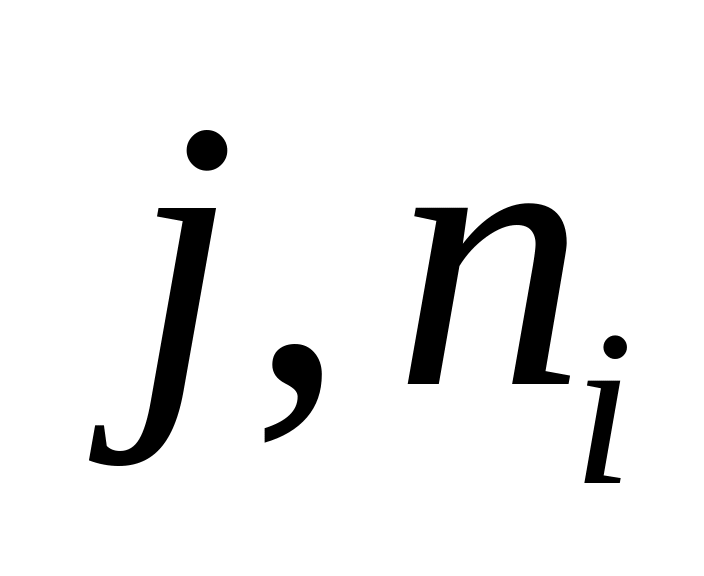 )
исключаются из графа G
или его компонента. Составляется таблица
связей
в виде объединений множеств
,
где
- включает номера операторов множества
J, исключая
.
Осуществляется переход на шаг 10.
)
исключаются из графа G
или его компонента. Составляется таблица
связей
в виде объединений множеств
,
где
- включает номера операторов множества
J, исключая
.
Осуществляется переход на шаг 10.Рассмотрим множество «к» компонентов графа G, образованного удалением связей. Если
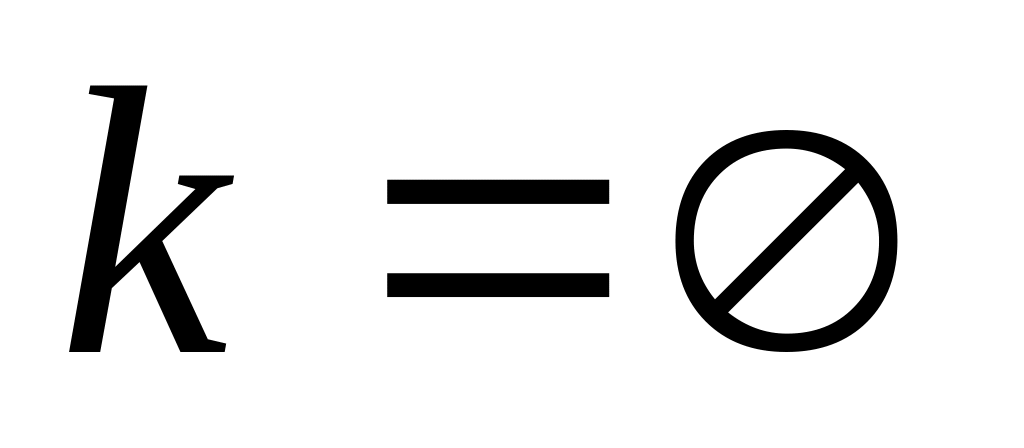 то переходим на шаг 16, Иначе выполняем
следующий шаг.
то переходим на шаг 16, Иначе выполняем
следующий шаг.С помощью матрицы S составленной для компонентов графа G, определим множество начальных вершин
 ,
таким образом, чтобы элементам множества
предшествовали элементы множества
,
таким образом, чтобы элементам множества
предшествовали элементы множества
![]()
![]() Переходим на шаг 2.
Переходим на шаг 2.
Для графа который имеет ту же конфигурацию, что и граф G, но в котором изменены веса вершин с учетом весов дуг, вычислим ранние сроки окончания операторов.
Для каждой нити
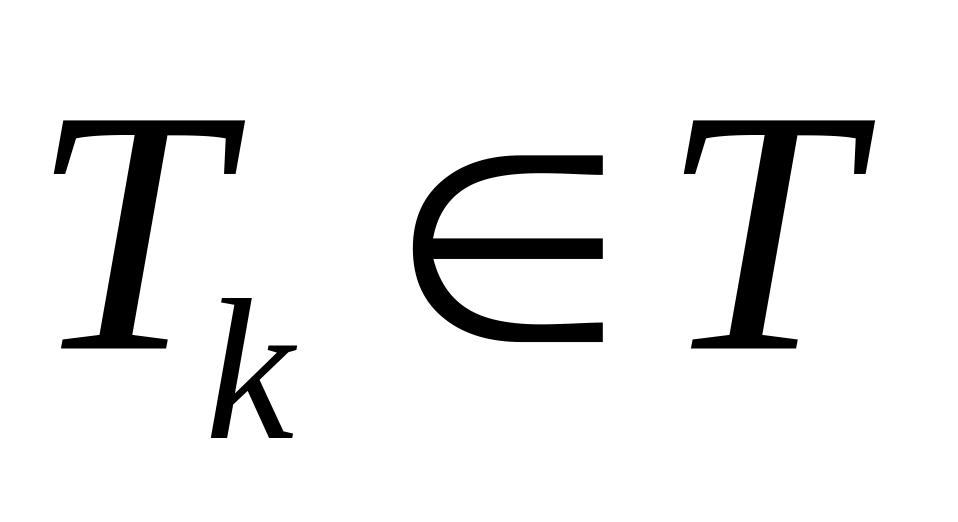 вычислим время старта
нити в виде
вычислим время старта
нити в виде
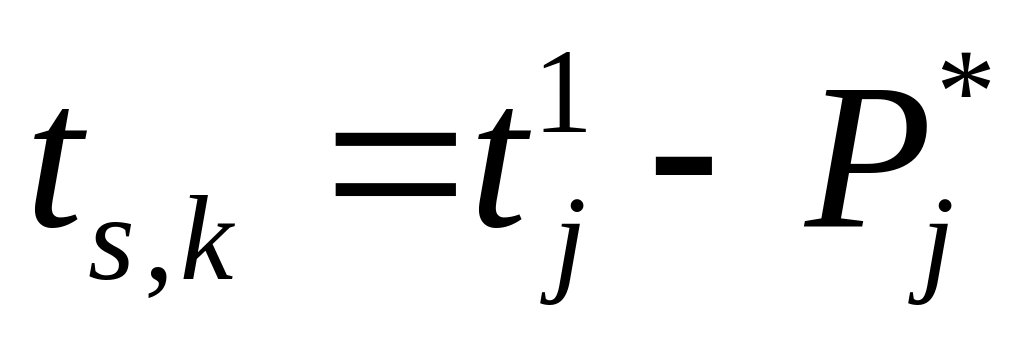 ,
где
,
где

Пример
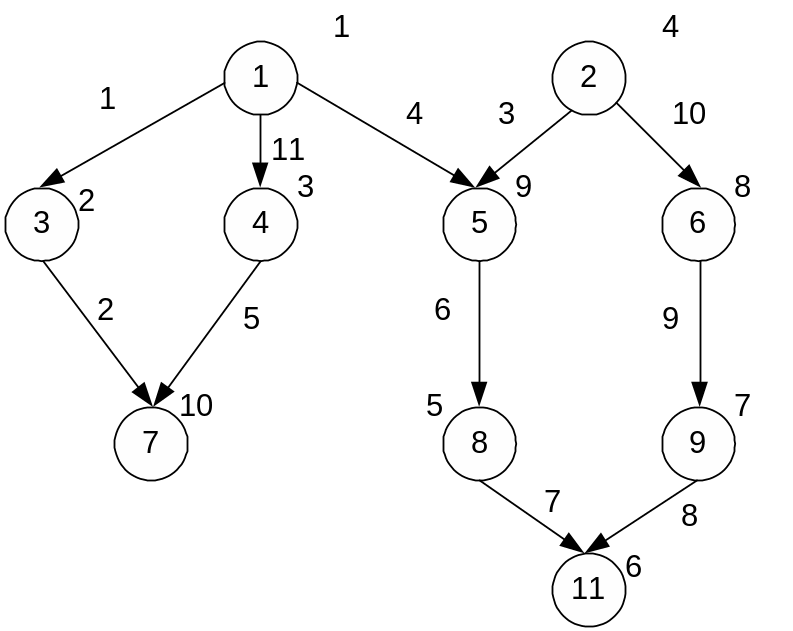
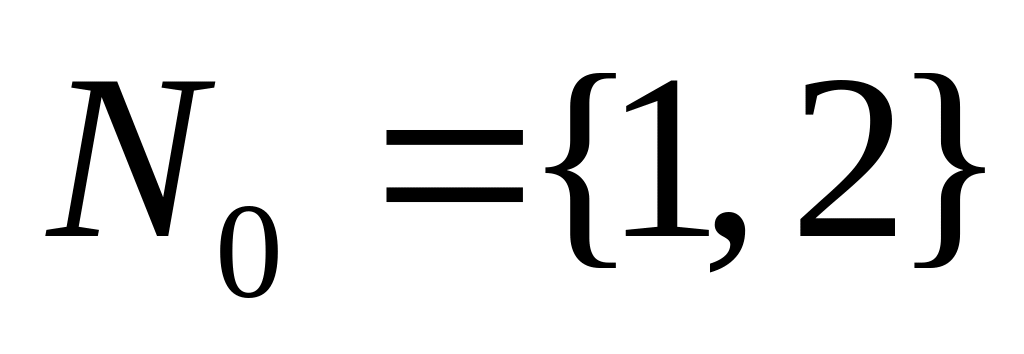
i:=1
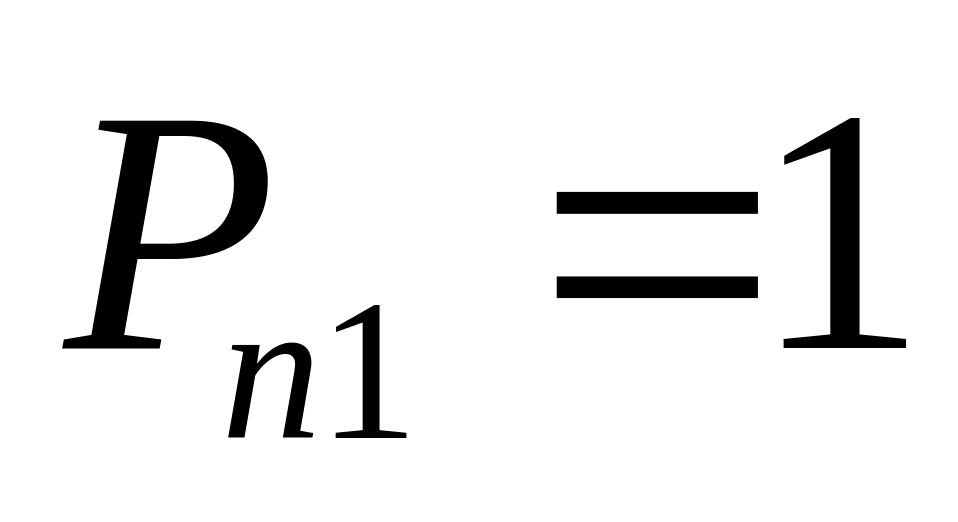
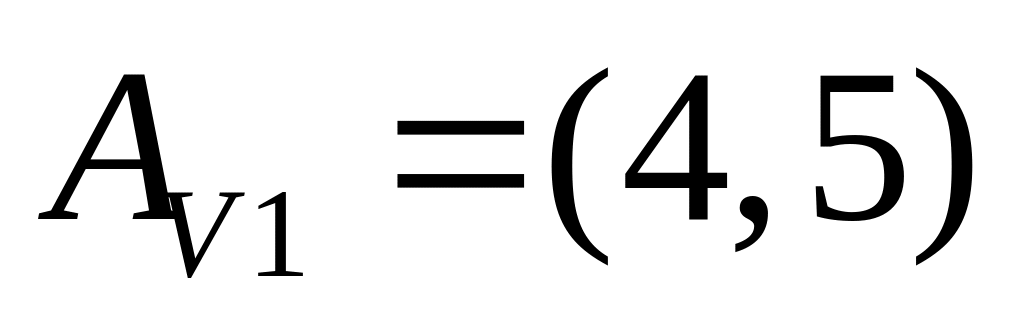
![]()
![]()

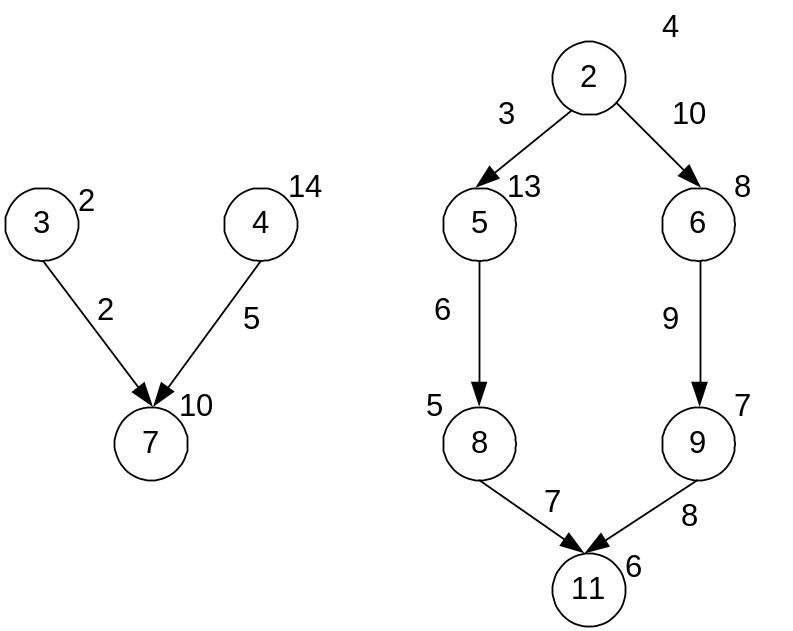
55. Представление алгоритмов взвешенными графами. Основные определения матрицы описания информационного графа. Алгоритмы ее получения.
56. Изображение схем параллельных алгоритмов с помощью информационных (иг) и информационно-логических (илг) графов.
ИГ используются для представления схем алгоритмов, не содержащих логические операторы. ИЛГ – для содержащих.
ИГ и ИЛГ представляются с помощью выражения G = (X, P, D), X –множество вершин i, X={1..m}. Это множество вершин графа, соответствующие множеству операторов параллельного алгоритма. P = {1..Pm} – множество весов вершин графа.
В общем случае Pi – вектор.
Если Pi - скаляр, то рассматривается решение этой задачи на однородной ВС ( с одинаковыми процессорами). Тогда Pi – время решения i-ой процедуры.
Если Pi – вектор, предполагается решение этой задачи на неоднородной ВС. И, тогда, если система содержит S разнотипных процессоров, то вектор Pi = { Pi1 ,… , Pis}, где Pi1 ,… , Pis – набор времен решения i-ой процедуры на нек-ом типе процессора из множества S.
D – множество дуг гафов. Дуги бывают двух типов: di Є D1, dj Є D2 , D = D1 U D2 .D1- множество информационных дуг графа. D2 – множество информационно-логических дуг графа.
ИЛ дуги графа исходят из логических блоков графа. И дуги графа исходят из выполняемых блоков графа. Дуги dj нагружены метками True или False.
Граф, содержащий только информационные дуги называется информационным графом.
Аналогично – ИЛГ. ИГ мы также будем называть информационный граф схемы алгоритма, аналогично ИЛГ.
ИГ: ИЛГ:
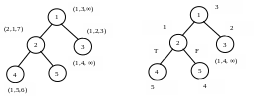
Нумерация в кружке – имя процедуры (номер вершины). Скобки – вектора весов (тут 3х мерные вектора) Номер позиции – тип процессора. ∞ - на этом процессоре данная процедура не выполняется.
Вычисление матриц следования, расширенных матриц следования и матриц следования с транзитивными связями.
Определение 1. Если в параллельном алгоритме существует связь между операторами α, β и α – исполнительный блок, то в графе G существует дуга di Î D1, исходящая из вершины α и входящая в вершину β. Эту связь будем обозначать α → β.
Определение
2. Если
в параллельном алгоритме существует
связь между операторами α, β и α –
логический блок, то в графе G
существует дуга di
Î
D2,
исходящая из вершины α и входящая в
вершину β. Эту связь будем обозначать
![]() или
или
![]() соответственно и называть связь по
управлению.
соответственно и называть связь по
управлению.
Связь
![]() определяет
связь между операторами, если оператор
α принимает значение “ TRUE
”, связь
- в противном случае.
определяет
связь между операторами, если оператор
α принимает значение “ TRUE
”, связь
- в противном случае.
Связи α → β, , назовём задающими связями.
Определение 3. Путями в графе G назовём последовательности вершин α1,…, αn , такие, что для любой пары вершин αi, αi+1 существует дуга uÎD1 U D2, исходящая из вершины αi и входящая в вершину αi+1.
В графе G нет циклов, поэтому все пути имеют конечную длину. Кроме того, будем считать, что значения логических переменных не связаны друг с другом, поэтому в процессе реализации алгоритма возможен любой из допустимых путей.
Определение 4. Характеристикой пути в графе G назовем количество вершин, входящих в этот путь.
Определение 5. Длиной пути в графе G со скалярными весами вершин назовем сумму весов вершин, составляющих этот путь.
Определение 6. Путь максимальной длины Ткр в графе G со скалярными весами вершин назовем критическим. В одном графе может быть несколько критических путей.
В качестве примера алгоритмов в виде схемы последовательного и параллельного алгоритмов с некоторыми трехмерными весами вершин представлен рис. 3.

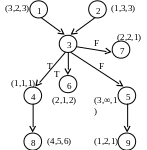
Нумерация блоков в последовательном алгоритме дана в соответствии с ярусностью. В качестве формального средства обработки графов введем матрицу следования S. В матрице следования для удобства использования в столбцах помечены значением 1 все выходящие из данной вершины связи, а в строках – все входящие в заданную вершину связи.
Более точное определение матрицы следования заключается в следующем: i –ой вершине графа G ставятся в соответствие i – ые столбец и строка матрицы, если существует связь по управлению , то элемент матрицы равен (i,j) = jT, порождает значение (i,j) = jF, при j → i образуется (i,j) = 1. Остальные элементы матрицы равны 0.
Если мы хотим сказать, что между элементом i и j существует некоторая связь, то будем писать i → j. Для отражения весов вершин вводится понятие расширенной матрицы следования SR: прибавляется дополнительно k столбцов с номерами m+1,…,m+k, где k – размерность вектора весов вершин граф – схемы.
1 |
|
|
|
|
|
|
|
|
|
3 |
2 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|
3 |
2 |
3 |
2 |
1 |
|
|
|
|
|
|
|
|
1 |
3 |
3 |
|
2 |
|
|
|
|
|
|
|
|
|
1 |
3 |
3 |
3 |
|
1 |
|
|
|
|
|
|
|
4 |
2 |
1 |
|
3 |
1 |
1 |
|
|
|
|
|
|
|
4 |
2 |
1 |
4 |
|
|
3T |
|
|
|
|
|
|
1 |
1 |
1 |
|
4 |
|
|
3T |
|
|
|
|
|
|
1 |
1 |
1 |
5 |
|
|
3F |
|
|
|
|
|
|
3 |
∞ |
1 |
|
5 |
|
|
3T |
|
|
|
|
|
|
3 |
∞ |
1 |
6 |
|
|
|
1 |
|
|
|
|
|
2 |
1 |
2 |
|
6 |
|
|
3F |
|
|
|
|
|
|
2 |
1 |
2 |
7 |
|
|
|
|
1 |
|
|
|
|
2 |
2 |
1 |
|
7 |
|
|
3F |
|
|
|
|
|
|
2 |
2 |
1 |
8 |
|
|
|
|
|
1 |
|
|
|
4 |
5 |
6 |
|
8 |
|
|
|
1 |
|
|
|
|
|
4 |
5 |
6 |
9 |
|
|
|
|
|
|
1 |
|
|
1 |
2 |
1 |
|
9 |
|
|
|
|
|
1 |
|
|
|
1 |
2 |
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
