Алгоритм A обеспечивает, наряду с требуемой обработкой, управление одновременной работой M процессоров с необходимым обменом данными между ними.

Структура коллектива вычислителей, представленных в виде графа:

GS=(M, S*), где М={m_i}, i= 0, …, N-1,

S_i,j S*, i, j= {0, …, N-1}.

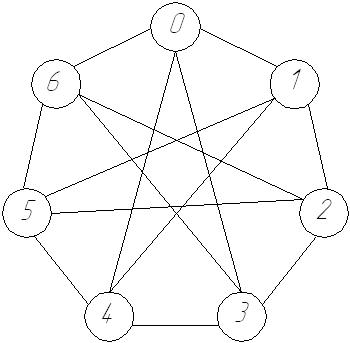
Симметричной ВС называется неориентированный граф, в котором произвольная нумерация вершин не меняет степень вершин графа, где под степенью вершины понимается количество ребер, примыкающих к ней.

Одними из важных параметров сети являются ее диаметр и средний диаметр, определяющие временные задержки при обмене информацией между процессорами сети.

Диаметр d – это максимальное расстояние, определяемое как

где – расстояние между вершинами i и j рассматриваемой сети.

Расстояние есть минимальная длина простой цепи между вершинами i и j, где длина измеряется в количестве ребер между вершинами i и j.

Средний диаметр для выделенной вершины n определяется как

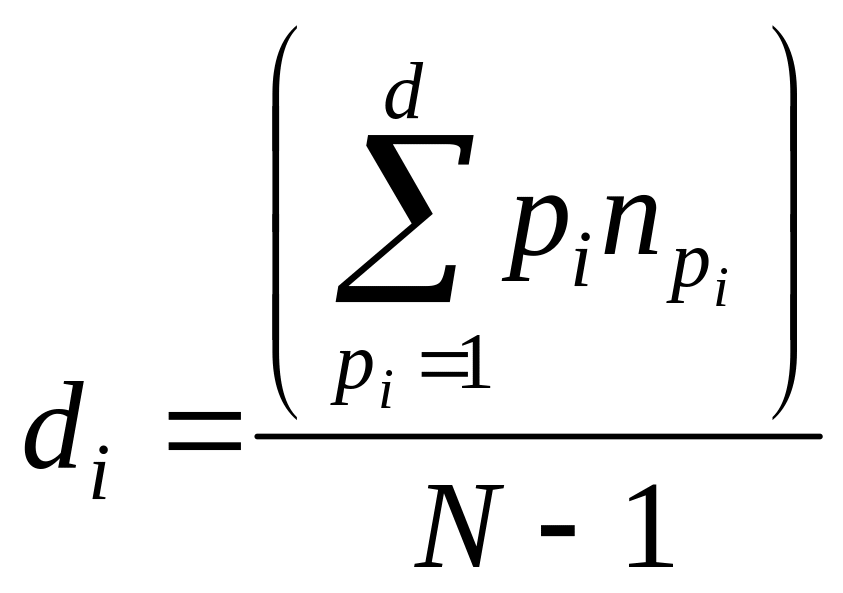, где p_i – расстояние от текущей вершины до выделенной (i-ой),

n_pi – число вершин, находящихся на расстоянии p_i от выделенной.

Средний диаметр сети : .

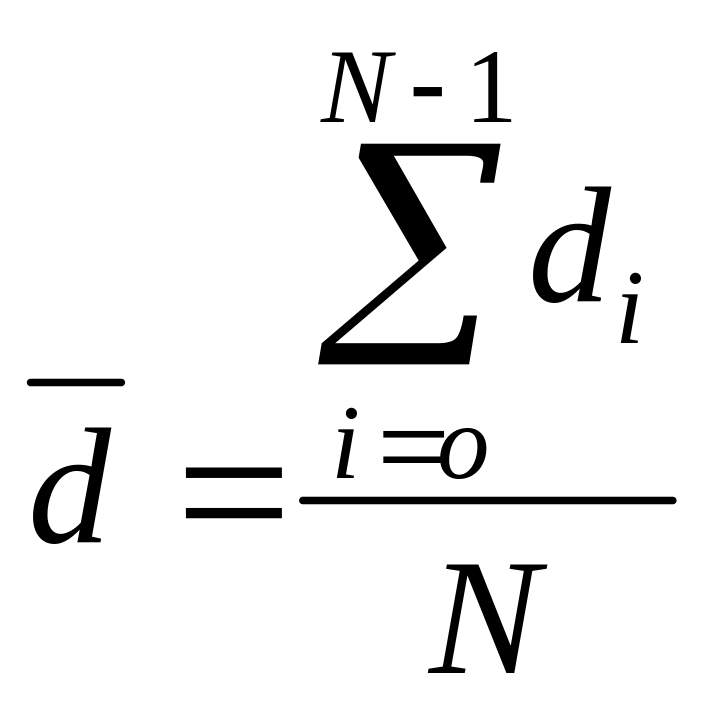Для симметричной сети .

3. Наиболее популярные схемы вычислительных систем: «общая шина», «линейка», «кольцо», «тор», «решетка».

Схемы обмена между вычислителями:

1. О бщая шина. Структура вычислительной сети типа «Общая шина» описывается графом GS=(M, S*), где M ={m_i}, i=0, …, N-1 – множество вычислителей, N≥3, S* в каждый момент времени t_k = {t₁, …, t_k} состоит из одного ребра S_i,j (i,j M), а множество вершин t_k определяет моменты реконфигурации сети.

2. Л инейка. Структура ВС типа «Линейка» описывается графом GS=(M, S*), где M ={m_i}, i=0, …, N-1 – множество вычислителей, N≥3, S* состоит из ребер S_i,(i+1), i=0, …, N-2.

*Каждый вычислитель кроме первого и последнего, связан друг с другом. Минус такой схемы: Отказ одного вычислителя приводит всю систему к сбою.

3. Кольцо. Структура ВС типа «Кольцо» описывается графом GS=(M, S*), где M ={m_i}, i=0, …, N-1 – множество вычислителей, N≥3, S* состоит из ребер S_i,(i+1)modN, i=0, …, N-1.

*Каждый вычислитель связан друг с другом. Функция mod(N) – строит ребро между первым и последним вычислителями.

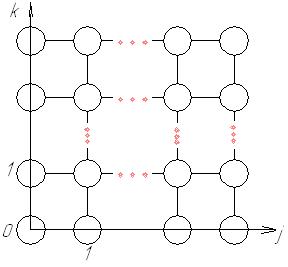
4. Решетка. Структура ВС типа «Решетка» описывается графом GS=(M, S*), где M={m_i}, i= 0, …,N-1, N>5; S* состоит из множества ребер S_i,k j {0, …,Y-1}, k {0, …, L-1}, причем L×Y=N.

Ребро проводиться между вершинами, определяемыми декартовым произведением [j] ×[k]. Две вершины соединяются ребром, если их декартовы произведения отличаются друг от друга на 1 по координате k или j соответственно.

5. Тор – см. след. вопрос.

4. Структура вычислительных систем типа двумерный тор, n-мерный двоичный гиперкуб.

Д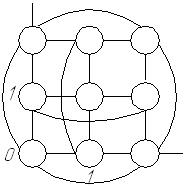 вумерный тор.

*Здесь между собой соединяются граничные вычислители (возможно, все), т.е. те, которые имеют max или min координату по одной из осей. (минус: появляются дополнительные шины). Другими словами можно сказать, что двумерный тор- это ВС «2D-решетка», противоположные грани которой соединены, обеспечивая обмен данными между первым и последним элементами строки/столбца.

Структура ВС типа «двумерный тор» описывается графом GS=(M,S*), где M= 0, …, N-1, N≥7; S* состоит из ребер S_i,k j {0, …,Y-1}, k {0, …, L-1}, причем L×Y=N.

Ребро проводиться между вершинами, определяемыми декартовым произведением [j] ×[k]. Две вершины соединяются ребром, если их декартовы произведения отличаются друг от друга на 1 по любой координате или на L-1 по координате k или на Y-1 по координате j.

n-мерный двоичный гиперкуб.

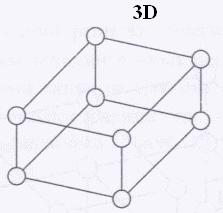
С 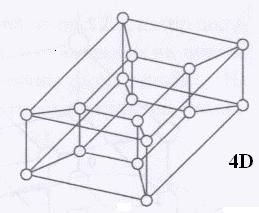труктура ВС типа «двоичный гиперкуб» описывается графом GS=(M,S*), где М={m_i}, i=0, …,N-1, N≥4, вершины имеют номера N_i=2^p, p=0,1,…,n-1, где n – размерность гиперкуба.

Каждая вершина V_i задается двоичным числом

q(V_i)=p_vi,0… p_vi,n-1.

Между вершинами V_i и V_j проводиться ребро, если их двоичные номера q(V_i) и q(V_j) различаются только одним разрядом.

5. Реализация обмена информацией в структуре типа «обобщенный nd-куб» и «nd-тор»

Обобщенный nd-куб.

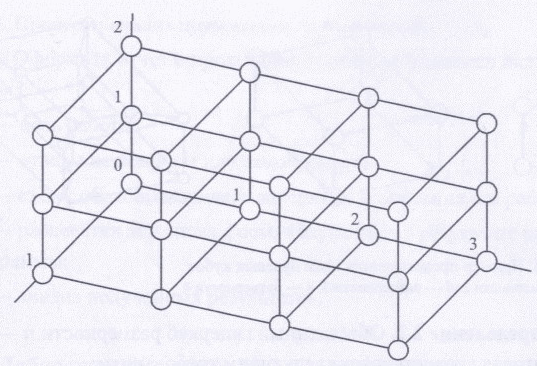Структура ВС типа «обобщенный nd-куб» описывается графом GS=(M,S*), где М={m_i}, i=0, …,N-1, N≥5.

По каждой координате j=1, …,n откладываются точки (вершины) с номерами 0,1,…,N_j-1, где N_j – размерность куба по координате j.

Множество вершин задается декартовым произведением [N₁-1] ×[N₂-1] ×…×[N_n-1]; N₁ ∙N₂ ∙…∙N_n=N. Две вершины соединяются ребром, если декартовы произведения отличаются друг от друга на 1 по координате N_j, j {1, …, n}.

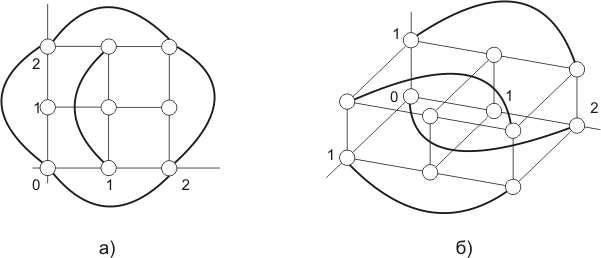
Обобщенный nd-тор.

Структура ВС типа «Обобщенный nd-тор» описывается графом GS=(M,S*), где М={m_i}, i=0, …,N-1.

По каждой координате j=1,…,n, вводятся точки 0,1, …, N_j-1, где N_j размерность тора по координате j.

Множество вершин графа задается декартовым произведением [N₁-1] ×[N₂-1] ×…×[N_n-1].

Множество ребер сети S* строиться следующем образом: две вершины соединяются ребром, если их декартово произведение отличается друг от друга на 1 или на N_j -1 по координате j. (картинки 2D и 3D на след. странице)

6. Структура вычислительных систем типа циркулянта и типа л(n,n,g) - граф.

Циркулянта.

П редставляется виде dn-графов, которые описываются Dn=G(N, q₁, …, q_n), где N –число вершин графа (вычислителей), которые нумеруются от 0 до N-1, q₁, …, q_n – образующие числа, такие что 0< q₁< q₂<…< q_n< . N, q₁, …, q_n – взаимно простые (наибольший общий делитель равен 1). n – число образующих чисел.

Вершина i соединяется ребрами с вершинами (i ± q₁)mod(N), …,(i ±q_n)mod(N).

Обычно циркулянта представляется в виде матрицы или хордового кольца.

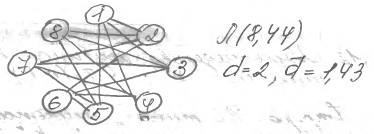
Л(N,ν,g).

N – количество вычислителей.

ν – степень вершин.

g – обхват графа (самый короткий контур (цикл) в графе).

Алгоритм построения такой структуры довольно сложен. Структура представляется в виде матрицы следования.

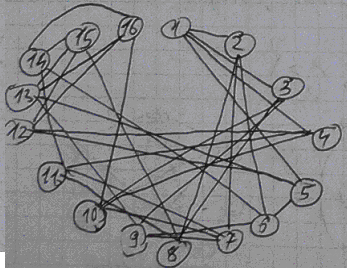
Структура ВС типа «Л(N,ν,g) – граф» описывается графом GS=(M, S*), где M={m_i}, i=0, …, N-1; S* – симметричная вычислительная сеть, описываемая матрицей смежности. В матрице смежности пишется: номер элемента – номера элементов, с которым он соединяется. (на рисунке Л(8,4,4) и Л(16,4,4))

7. Структура вычислительных систем типа «бинарное дерево», «мультидерево глубины n и ширины k».

Б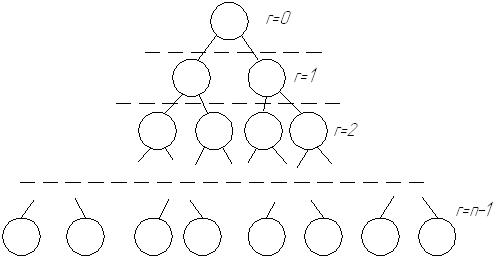 инарное дерево T_o(n).

Структура ВС типа «бинарное дерево» обозначается T_o(n) глубины n описывается графом GS=(M, S*), где M={m_i}, i=0, …, N-1, N=2ⁿ-1;

Содержит n рангов r (r={0, …,n-1}), причем в каждом ранге размещается ровно 2^r вершин так, что каждая вершина ранга r (0<r<n-2) соединяется с парой вершин ранга r+1.

Мультидерево глубины n и ширины k T₁(n, k).

С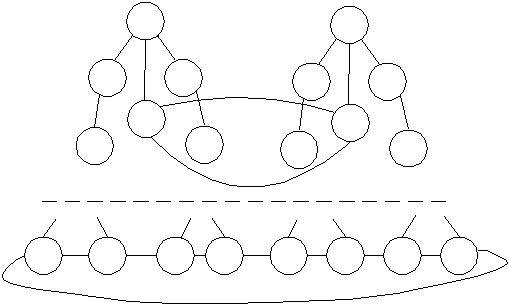 труктура ВС типа «Мультидерево глубины n и ширины k» T₁(n, k), число вычислителей N=k*2ⁿ описывается графом GS=(M, S*), где M={m_i}, i=0, …, N-1, а сеть S* содержит k двоичных деревьев, объединенных с помощью колец R₀ и R_1.

К орневая вершина j={1, …,k} каждого из k деревьев соединена ребром с вершиной и они образуют кольцо R₀ ( , , …, ). Второе кольцо R₁ образованно вершинами листьев и содержит k*2^n-1 элементов.

8. Характеристика коммутаторов вычислительных систем.

Наиболее часто используются следующие:

1. Простые коммутаторы с временным разделением (с общей шиной);

2. Простые коммутаторы с пространственным разделением.

3. Сосредоточенные составные коммутаторы.

4. Распределенные составные коммутаторы.

Коммутаторы с пространственным разделением: n входов и m выходов. Например, n=m=2.

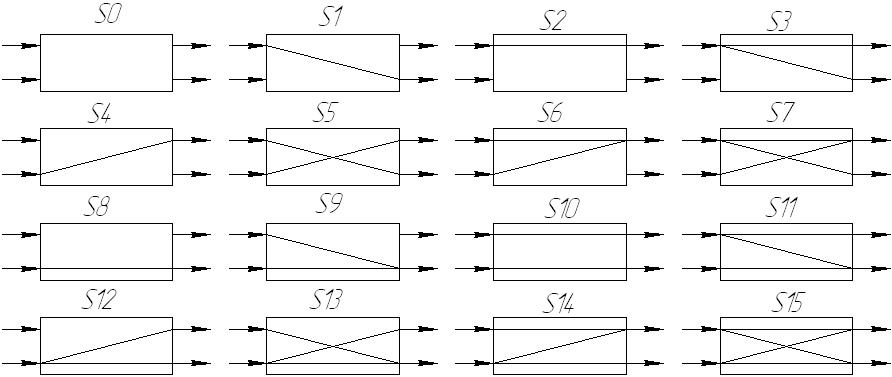
Количество состояний коммутатора Q=2^k, где k –количество связей в коммутаторе.

k=1 (S1, S2, S4, S8) – простые коммутаторы 1-го типа.

k=2 (S3, S5, S6, S9, S10, S12) – простые коммутаторы 2-го типа.

k=3 (S7, S11, S13, S14) – простые коммутаторы 3-го типа.

k=4 (S15) – простые коммутаторы 4-го типа (коммутатор Клоза –соединяет n входов и m выходов).

Баньян-сети: существует путь от каждого из n входов к каждому из m выходов (S5).

Коммутаторы объединяются в цепочки для создания более сложных.

Коммутаторы, управляемые с помощью программы, называются транспьютерами( коммутаторы с программируемой архитектурой, или динамические). Не управляемые с помощью программ – статические.

9. Архитектурные свойства вычислительной сети и описание процессов её функционирования.

Описание процесса функционирования сети.

Сеть функционирует с помощью алгоритма А, который управляет вычислителями С_i C, i=0, …, N-1 на сети G. В алгоритм А входит совокупность программ: , причем , которые осуществляют вычисления. Набор данных: , – для каждой программы свой.

Алгоритм А представляется совокупностью: , где – вычислительная часть, а – обеспечение связи через сеть.

– обеспечивает аппаратно-программную часть.

Аппаратные средства, с помощью которых реализуется совокупность алгоритмов A_i, i=0,…,N-1, и которые вместе с сетью связей составляют среду для осуществления взаимодействия между вычислителями ВС, называются коммутаторами.

Программно-аппаратные средства, с помощью которых реализуется совокупность программ P_i, i=0,…,N-1, и которые вместе с сетью связей составляют среду для осуществления взаимодействия между вычислителями ВС, называются коммутаторами с программируемой структурой.

У большинства ВС алгоритмы A_i=A_j, i, j=1, …,N-1, и программы Р_i=Р_j. Такие системы называются однородными. На них можно решать любые задачи, но лучше всего – решать ДУ, находить коэффициенты Фурье.

Принципы технической реализации ВС.

При технической реализации ВС используются принципы модульности и близкодействия.

Принцип модульности заключается в следующем: ВС формируется из унифицированных модулей M_i, где R – количество разнообразных моделей в системе. Каждый модуль функционально закончен; имеются модули сопряжения. Набор модулей представляет функционально законченный набор процессоров, что означает, что можно решать любую задачу. Помимо полного набора M_i, может быть набор M_in, т.е. можно брать подмножество из множества M_i и получать другую ВС с другими характеристиками.

Модульность обеспечивает:

1. возможность использования любого модуля для выполнения любого соответствующего задания пользователя.

2. простая замена одного модуля на однотипный.

3. масштабируемость – можно уменьшить или увеличить количество модулей без коренной реконфигурации связей между остальными модулями.

4. открытость систем для модернизации, что исключает ее моральное старение.

В системах с массовым параллелизмом, в которых есть только один модуль, обладающий вычислительной и соединительной полнотой, то, что стоит в узле, называется элементарным процессором (машиной); его разрядность колеблется от 1 до 64.

Близкодействие обуславливает такую организацию информационного взаимодействия между модулями вычислителя, при которой каждый из них может непосредственно обмениваться информацией с весьма ограниченной частью модулей вычислителя, следовательно, структура ВС позволяет осуществлять взаимодействие между удаленными вершинами вычислителя лишь с помощью промежуточных вершин вычислителя, передающих информацию от точки к точке. Удаленными считаются вершины, расстояние между которыми >1.

Принцип близкодействия допускает реализацию механизма управления ВС, не зависящего от числа вычислителей. Данный принцип, в частности, выражается в том, что поведение каждого вычислителя С_i C зависит только от ограниченного подмножества С^* C.

Во взаимосвязи с принципом близкодействия говорят о локальной связи вычислителя. Последнее означает, что состояние вычислителя С_i на очередном временном шаге (t+1) зависит от состояния на предыдущем шаге t вычислителей С_j C^*, непосредственно связанных с ним.

Т.о., состояние Е_i на шаге (t+1) есть функция: , т.е. состояние вычислителя зависит от его локального окружения.

ВС основанные на принципах модульности и близкодействия, обладают рядом ценных свойств, таких как децентрализованность, асинхронность и распределенность.

Асинхронность: функция ВС обеспечивается, если порядок срабатывания ее модулей определяется не с помощью выработанных тем или иным образом отметок времени, а достижением заданных значений.

Использование асинхронных схем позволяет достичь в системе алгоритмически предельного быстродействия. Модули ВС срабатывают немедленно после достижения соответствующего условия. Применение асинхронных схем обмена информацией между вычислителями позволяет не учитывать разброс в их тактовых частотах и длительностях импульсов сигналов линей связи.

Архитектурные свойства ВС.

Имеется ряд свойств ВС, которые обеспечивают ей значительные преимущества перед раннее создаваемыми вычислительными комплексами. К таким свойствам относят:

1. Масштабируемость. Обеспечивает способность к наращиванию и сокращению производительности ВС, что дает возможность в течение длительного времени быть адекватным средством решения сложных задач. Это означает, в частности, что производительность, достигнутую на заданном количестве вычислителей, можно увеличить, подключив к ВС новые вычислители. Свойство наращивания производительности представляет потенциальную возможность решать задачи любой сложности.

2. Универсальность. Обеспечивается тем, что она состоит из вычислителей, поэтому любая задача, для которой составлен алгоритм, может быть решена на ВС с той или иной степенью эффективности – сколько вычислителей может быть использовано для решения поставленной задачи и насколько хорошо распараллеливается заданный алгоритм.

3. Производительность ВС достигается за счет усложнения структуры. Пределы увеличения производительности полностью зависят от масштабируемости.

4. Реконфигурируемость ВС бывает статической и динамической. В статическом режиме приспособление структуры ВС под класс решаемых задач (выбор количества вычислителей, структуры сети), определяется предварительно на этапе подготовки задачи к выполнению. При этом возможно, при наличии времени, оптимальный или квазиоптимальный подбор конфигурации сети. При решении задач в случае дефицита времени конфигурация сети определяется динамически на основе быстро решаемых эвристических алгоритмов.

5. Надежность и «живучесть». (см. след. вопрос)

6. Самоконтроль и самодиагностика.

Важным фактором функционирования ВС является самоконтроль и самодиагностика, что обеспечивает и высокую надежность и «живучесть». В качестве контрольно-диагностического подмножества ВС может быть использованы любые исправные вычислители, а в пределах этого подмножества – любой вычислитель. Выбор диагностического подмножества ВС производиться, как правило, автоматически.

7. Технико-экономическая эффективность.

Не менее ценным свойством ВС является конструктивная однородность , что резко увеличивает её технико-экономическую эффективность. Это свойство ВС позволяет резко снизить сроки ее разработки, и приводит к повышению технологичности производства, упрощает статическую и динамическую реконфигурацию, облегчает техническую эксплуатацию.

10. Надежность и живучесть вычислительной системы.

Под надежностью вычислительной сети понимается ее способность к автоматической настройке и функционированию таких структурных схем, которые при отказах и восстановлениях вычислительной сети обеспечивают заданный уровень производительности.

Отказ – событие, при котором система теряет способность выполнять функции, связанные с реализацией параллельной программы, с заданным числом ветвей. Если вычислительная сеть находится в состоянии отказа, то число неисправных вычислителей превосходит число вычислителей, составляющих структуру избыточности.

Под живучестью вычислительной сети понимается свойство вычислительной сети, которое в условиях отказов и восстановления вычислительной сети гарантирует производительность в заданных пределах при выполнении параллельной программы даже в случае отсутствия зарезервированных вычислителей.

Полный отказ – событие, состоящее в том, что система теряет способность к выполнению параллельной программы.

Частичный отказ – событие, при котором имеет место отказы вычислителей, однако сохраняется возможность реализации на вычислительной сети параллельной программы.

11А. Схемы обмена информацией между ветвями параллельных алгоритмов.

1. Дифференцируемый обмен (1 источник, 1 приемник; Малоэффективен).

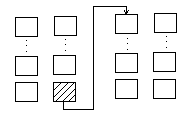
2. Трансляционный обмен (1 источник, все приемники). (one to all broadcast)

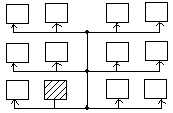
3. Трансляционно-циклический обмен – источник постоянно «двигается». Тот, кто был приемником, становиться источником, и наоборот. (за n тактов) (all to all broadcast)

4. Конвейерно-параллельный обмен – все нечетные номера становятся источниками, а четные – приемниками, а затем они меняются. (за 2 такта)

5. Коллекторный (по сути – инвертированный трансляционный обмен). Вычислитель передатчик становится приемником. В одну ветвь собирается информация из l≤ n ветвей. Такой обмен требует n тактов и реализуется как последовательность n дифференцируемых обменов.

Имеется статистика частоты использования схем обмена информацией при реализации крупноблочных параллельных алгоритмов. Которая представлена в таблице:

Тип обмена	ДО	ТО	ТЦО	КПО	КО
Частота использования	2%	17%	40%	34%	7%

12. Структурные характеристики вычислительных систем.

1. Структурные задержки при передаче информации между узлами характеризуются d и 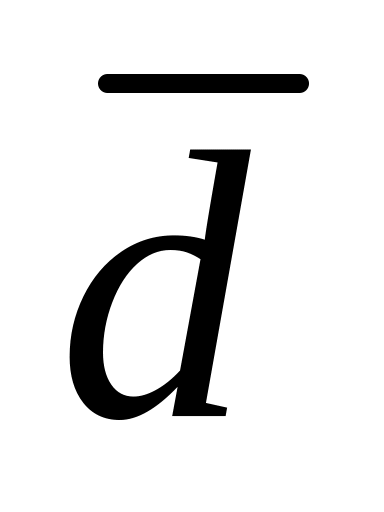ВС.

2. Структурная коммутируемость. Характеризуется вектор-функцией:

Координата - вероятность реализации в системе вероятности одновременных непересекающихся межмашинных взаимодействий (n) при заданной структуре сети G и коэффициенту готовности S вычислителя и коэффициенту готовности сети.

Структурная коммутируемость характеризует способность ВС к параллелизации обмена между вычислителями. При этом требуется чтобы:

• При дифференцируемом обмене имелась возможность реализации 1 обмена между двумя вычислителями.

• При трансляционном обмене реализовалась одновременная передача информации от одного вычислителя во все остальные.

• При конвейерно-параллельном обмене выполнялось одновременно 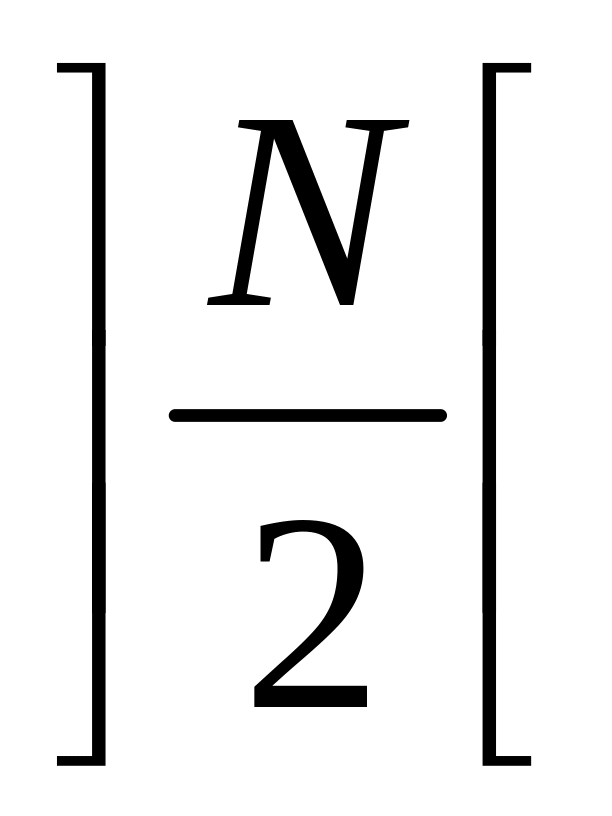взаимодействий между парами вычислителей.