3.4 Работа движущих сил

Примем, что приведенный движущий момент является постоянной величиной, тогда его работа равна:

где – приведенный момент движущих сил.

Т.о. график зависимости А_дв = f(φ₁) представляет собой наклонную прямую, проходящую через точки с координатами: (φ₁ = 0, А_дв = 0) и (φ₁ = 2π, А_дв = –А_с), т.к. для механизмов периодического движения за цикл работы движущих сил равна работе сил сопротивления.

3.5 Полное приращение кинетической энергии механизма

Полное приращение кинетической энергии можно определить из основного уравнения движения механизма для установившегося движения:

ΔТ = А_дв – А_с,;

Где: А_дв > 0 и А_с < 0.

Т.е. вычитая графически из ординат графика А_дв = f(φ₁) ординаты графика А_с = f(φ₁) и умножая полученную разность на масштабный коэффициент μ_А = 30 (Дж/мм), получаем значение ΔТ_i для каждого положения, которые заносим в таблицу 3.1.

Рассчитаем полное приращение кинетической энергии для главного положения – 1:

График зависимости ΔТ = f(φ₁) строим при масштабном коэффициенте и μ_Т = 30(Дж/мм).

3.6 Приведенный движущий момент, мощность электродвигателя

Графически дифференцируя полученный график А_дв = f(φ₁) при выбранном ранее полюсном расстоянии Н = 500 мм, строим графика = f(φ₁), который представляет собой прямую линию, параллельную оси φ₁. При этом , где h = 16 мм – ордината графика = f(φ₁).

Определим потребную мощность на валу кривошипа:

Потребная мощность на валу электродвигателя:

,

где η = 0,85 – коэффициент полезного действия передаточного механизма от двигателя к кривошипу.

3.7 Выбор электродвигателя, определение приведенного момента инерции ротора электродвигателя

По заданной синхронной частоте вращения и потребной мощности электродвигателя Р_дв = 3.2кВт выбираем по каталогу [1] электродвигатель со следующими параметрами:

– тип электродвигателя – 4А100S4У3;

– номинальная мощность электродвигателя Р_дв = 3,2 кВт;

– номинальная частота вращения ротора электродвигателя n_дв = 1435 мин^-1;

– маховый момент ротора GD² = 34·10^-2 кГ·м²;

Определим момент инерции ротора электродвигателя по формуле:

Приведенный к валу кривошипа момент инерции ротора электродвигателя равен:

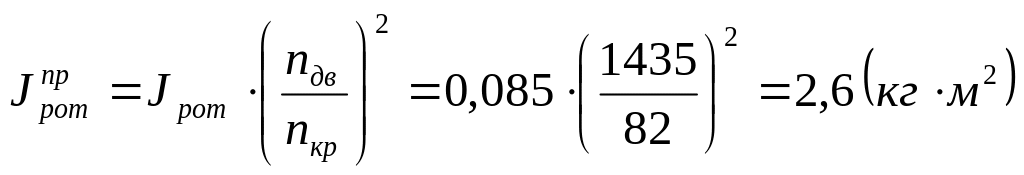
3.8 Приведенный момент инерции звеньев механизма

Приведенный к входному звену момент инерции звеньев всего механизма определяется из условия равенства кинетических энергий приведенной и приводимой масс.

,

где T_i – кинетическая энергия i-го звена механизма.

Расчетная формула приведенного к входному звену момента инерции звеньев для рассматриваемого рычажного механизма имеет вид:

, (3.5)

где – приведенный момент инерции i-го звена механизма, который определяется по формуле: ,

где ₁ – угловая скорость входного звена;

_i – угловая скорость i-го звена;

– скорость центра масс i-го звена;

m_i – масса i-го звена;

– центральный момент инерции i-го звена.

Для рассматриваемого механизма имеем:

;

.

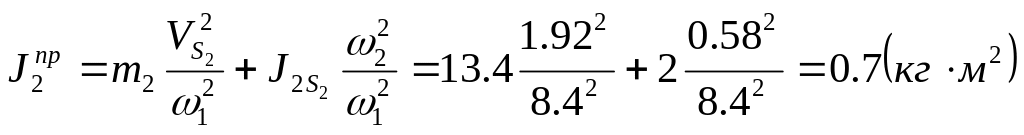
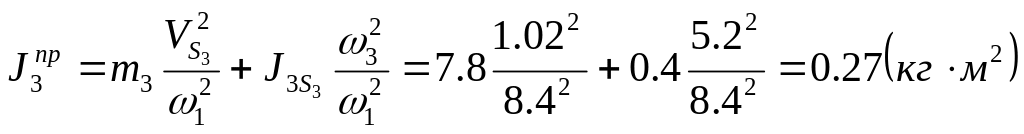
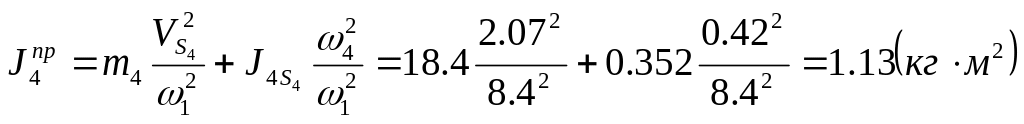
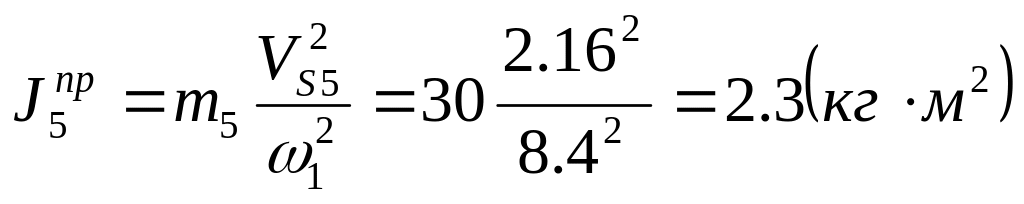Рассчитаем проведенный момент инерции для основного положения – 1:

По формуле (3.5):

.

Аналогично получаем значения для всех остальных положений механизма. Результаты расчетов сводим в таблицу 3.1.

По данным таблицы 3.1 строим график при μ_J = 0,03 (кг·м²)/мм.