
3) Свёртка
Свёртка двух бесконечных дискретных послед-тей {x1(k)} и {x2(k)} опр-ся следующим образом:
![]()
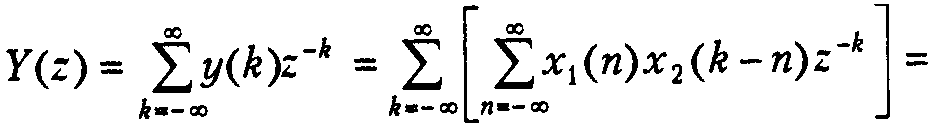
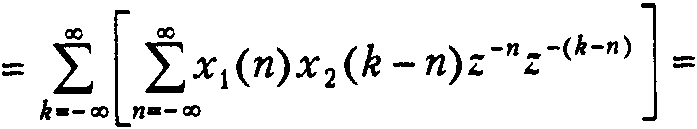
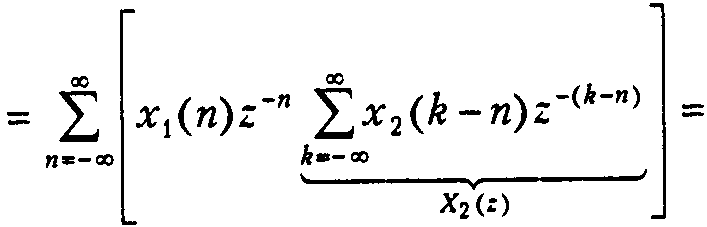
![]()
То есть свёртке дискретных последовательностей соответствует произведение их Z – преобразований.
Обратное Z – преобразование
Формула перехода от z- преобразования к последовательности чисел:
![]()
Интеграл берётся по произвольному замкнутому контуру, расположенному в области сходимости X(z), и охватывающему все её полюсы.
Практическое вычисление обратного Z – преобразования чаще производится путём разложения ф-ии X(z) на простые дроби.
Пример: пусть
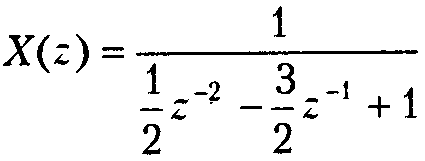
Представим X(z) в виде простых дробей:
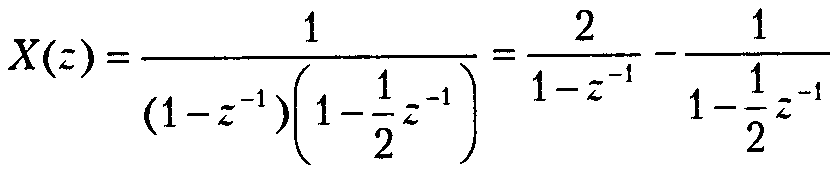
Из примеров, рассмотренных ранее видно, что первое слагаемое соотв-ет скачку с амплитудой = 2, а второе слагаемое – дискретной показательной ф-ии -2-k, k≥0
То есть искомая послед-ть имеет вид:
![]()
№8
Изменение частоты дискретизации
Часто приходится увеличивать или уменьшать частоту дискретизации сигналов.
В зависимости от значения коэффициента изменения частоты выделяют варианты:
1) Интерполяция – повышение частоты дискретизации в целое число раз
2) Прореживание – понижение частоты дискретизации в целое число раз
3) Передискретизация – изменение частоты дискретизации в произвольное (дробное) число раз
Прореживание
Казалось бы, для понижения частоты дискретизации в N раз, можно просто взять из исходной послед-ти каждый N отсчёт. Но при этом могут возникнуть побочные эффекты, например появление ложных частот (алясинг).
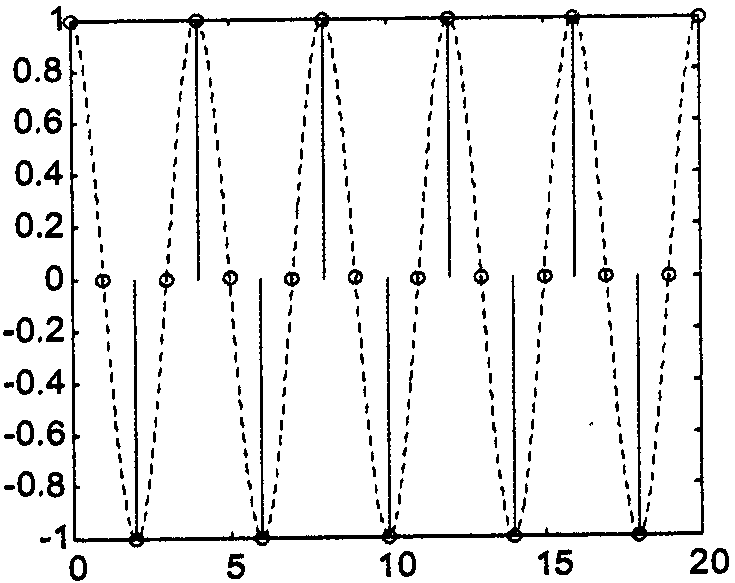
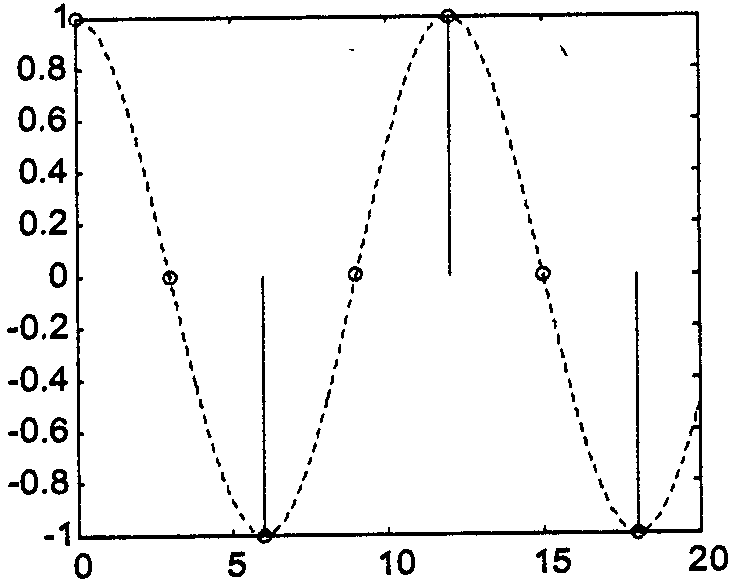
![]()
Таким образом, если в спектре исходного сигнала содержатся частоты, превышающие половину новой частоты дискретизации (т.е. новую частоту Найквиста), это приведёт к появлению в спектре выходного сигнала ложных частотных составляющих.
Для устранения этого эффекта, надо предварительно пропустить исходный сигнал через ФНЧ с частотой среза, равной новой частоте Найквиста.
А затем уже взять каждый N отсчёт (как описано в начале).
Интерполяция
При интерполяции необходимо повысить частоту дискретизации в N раз, то есть «растянуть» входной сигнал, а образовавшиеся промежутки между отсчётами чем-то заполнить.
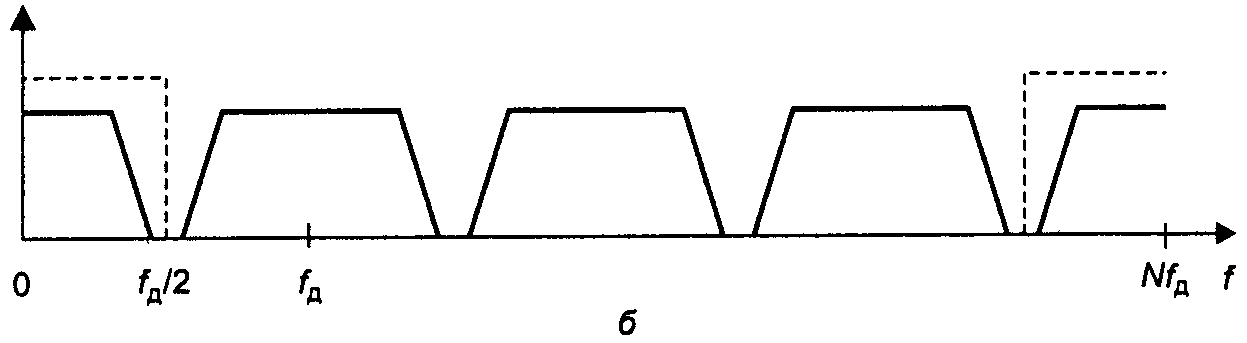
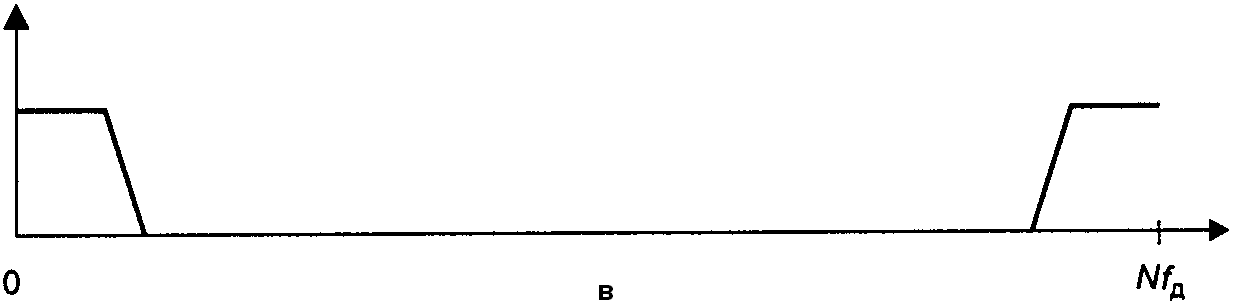
Исходный сигнал имеет периодический спектр, повторяющийся с частотой дискретизации fд (рис. 4.22, a). (На рисунке нарисован только один из периодов). Прежде всего мы «растягиваем» этот сигнал, добавляя между его отсчётами по N-1 нулей. При этом частота дискретизации сигнала станет равной Nfд, но период повторения сигнала останется прежним fд (рис. 4.22, б). Теперь необходимо пропустить полученный сигнал через ФНЧ с частотой среза fд/2 (его идеализированная АЧХ показана на рис. 4.22, б, пунктирной линией). В результате фильтрации получится интерполированный сигнал, у которого частота дискретизации равна Nfд, а спектр в полосе частот от нуля до fд/2 прежним (рис. 4.22, в).
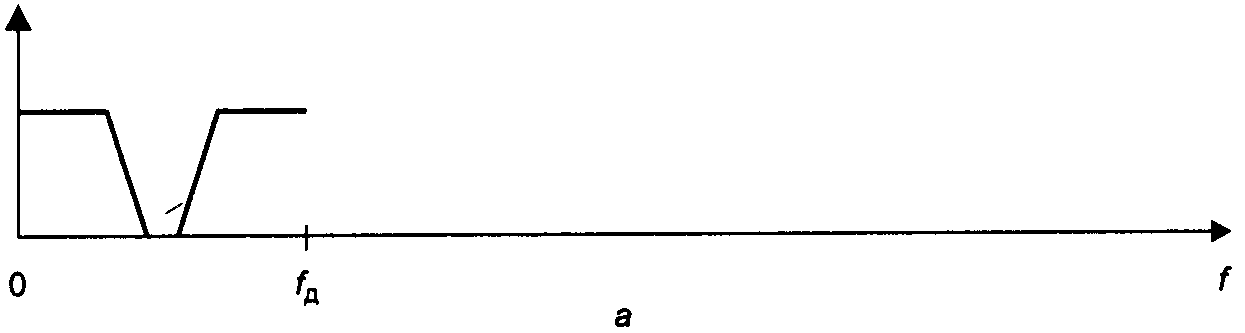
![]()
Передискретизация
Когда частота дискретизации меняется в нецелое число раз.
Явл-ся сочетанием интерполяции и прореживания.
Если исходную частоту дискретизации необходимо умножить на n/m, сначала выполняется интерполяция с коэффициентом n, а затем прореживание с коэффициентом m.
