Эргодические случайные процессы

Стационарный случайный процесс наз-ся эргодическим, если при определении любых его статистич. хар-к усреднение по множеству реализаций эквивалентно усреднению по времени одной, теоретически бесконечно длинной, реализации.

Обозначим усреднение по времени угловыми скобками.

X(t) - одна из реализаций случайного процесса.

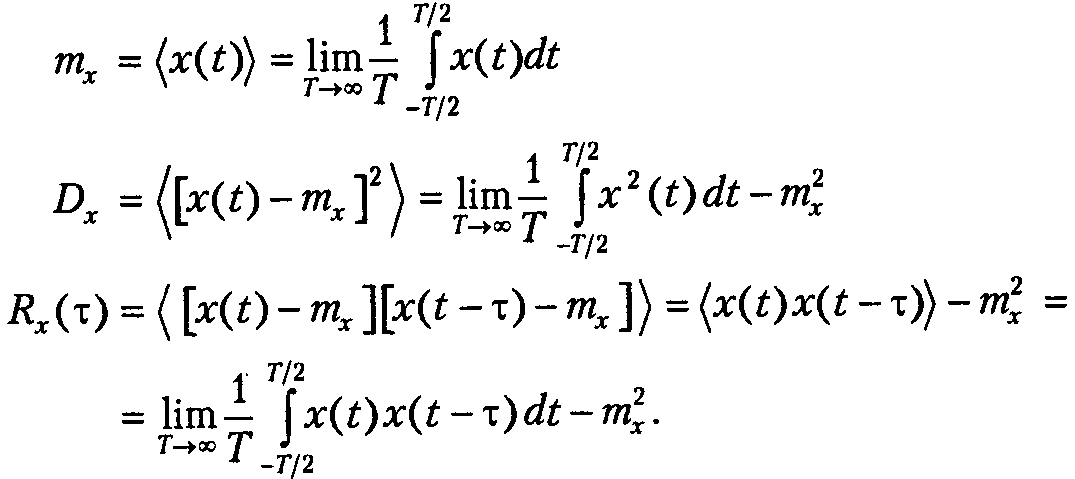
Достаточное условие эргодичности случ. проц., стационарного в широком смысле:

----------------------------------------------------------------------------------------------------

Проверим эргодичность гармонического процесса со случайной начальной фазой:

Параметры, вычисленные усреднением по времени, совпали с параметрами, полученными ранее путём статистического чсреднения. Сл-но, процесс явл-ся эргодическим.

№4

Линейными наз-ся системы, для которых вып-ся принцип суперпозиции: реакция на сумму сигналов равна сумме реакций на эти сигналы, поданные на вход по отдельности.

Если произвольная задержка подаваемого на вход сигнала приводит лишь к такой же задержке вых-го сигнала, не меняя его формы, система наз-ся стационарной.

Будет рассматривать только стационарные линейные системы.

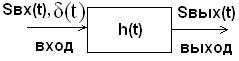
Импульсная характеристика

Можно найти реакцию системы на любой сигнал, зная всего одну функцию – реакцию системы на поданную на вход дельта – функцию. Эта реакция наз-ся импульсной хар-кой системы: h(t).

Любой сигнал может быть представлен в виде свёртки самого себя с дельта ф-ей:

Линейная система преобразует отн-но переменной t все ф-ии, входящие в это выражение.

S_вх(t) превр-ся при этом в выходной сигнал Sвых(t), а дельта ф-ия превр-ся в импульсную хар-ку:h(t-t’). Ф-ия S_вх(t’) от t не зависит, поэтому остаётся без изменений. В рез-те получаем формулу:

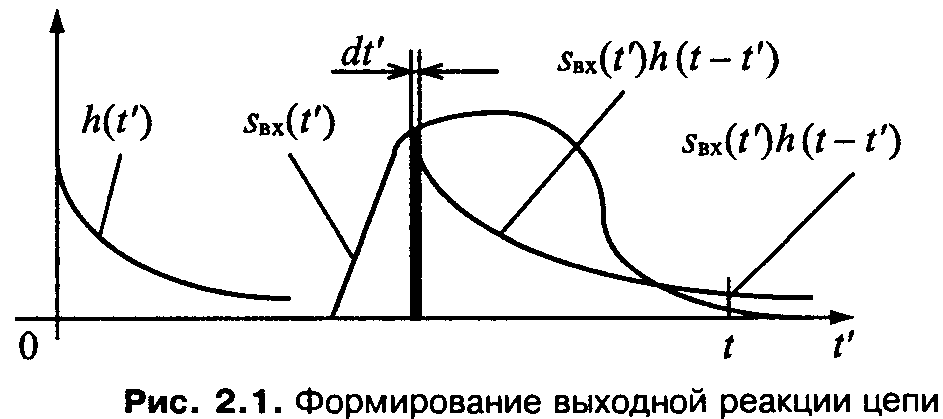
Формир-ие вых-го сигнала можно пояснить так:

Бесконечно малый «кусочек» вх. сигнала S_вх(t’) шириной dt’ порождает на выходе отклик, представляющий собой импульс. хар-ку, умноженную на S_вх(t’)dt’, и задержанную по времени на t’, то есть

Чтобы получить значение выходного сигнала в момент времени t, нужно сложить вклады от всех этих бесконечно малых «кусочков», то есть выполнить интегрирование по t’, что и даёт приведённую выше формулу свёртки.

Переходная хар-ка

П ереходной хар-кой наз-ся реакция системы на поданную на вход ф-ию единичного скачка. Переходная хар-ка обозн-ся как g(t).

Поскольку дельта ф-ия это производная от единичного скачка:

, то импульсная и переходная хар-ки связаны друг с другом дифференцированием и интегрированием:

Условие физической реализуемости

Любая физически реализуемая сстема обладает свойством причинночти – выходная реакция не может возникнуть раньше входного сигнала. Отсюда следует, что для физически реализуемой системы импульсная и переходная хар-ки дожны быть равны нулю при t<0:

h(t)=0, при всех t<0

g(t)=0, при всех t<0

№5

Комплексный коэффициент передачи

Выходной сигнал линейной системы предст-ет собой свёртку входного сигнала и импульсной хар-ки:

Преобразование Фурье от свёртки даёт произведение спектров сворачиваемых сигналов, так что в частотной области прохождение сигнала через линейную систему описывается просто:

- это преобразование Фурье импульсной хар-ки системы:

- эта ф-ия наз-ся комплексным коэффициентом передачи системы.

Её модуль A_k(ω) – это амплитулно – частотная хар-ка ситемы (АЧХ)

Её фаза φ_k(ω) – это фазочастотная хар-ка системы (ФЧХ)

Значение K(ω) показывает, как изменяется при прохождении через систему комплексная амплитуда синусоиды с частотой ω.

АЧХ показ-ет, во сколько раз изменится амплитуда синусоиды.

ФЧХ – каков будет полученный ей фазовый сдвиг.

Коэффициент передачи по мощности

Мощность гармонического сигнала пропорциональна квадрату его амплитуды и не зависит от его фазы. Поэтому коэффициент передачи по мощности равен квадрату модуля комплексного коэфф-та передачи, т.е. квадрату АЧХ:

Фазовая и групповая задержка

При преобр-ии сигнала линейной системой различают 2 вида задержки:

Фазовая задержка на частоте ω – задержка гармонич-го колебания с частотой ω, проходящего через систему:

Если задержку нельзя представить в виде одной гармоники, то говорят о групповой задержке :

№6

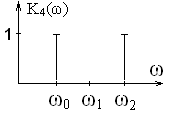
Пусть есть три синусоидальных сигнала с различной частотой :

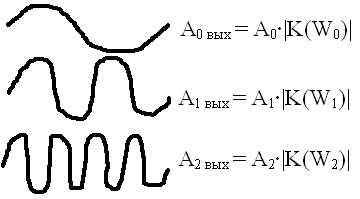
Линейная аналоговая система выглядит так:

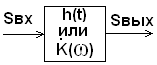
Посмотрим, каким комплексным коэффициентом передачи должны обладать фильтры, чтобы пропускать те или иные синусоиды.

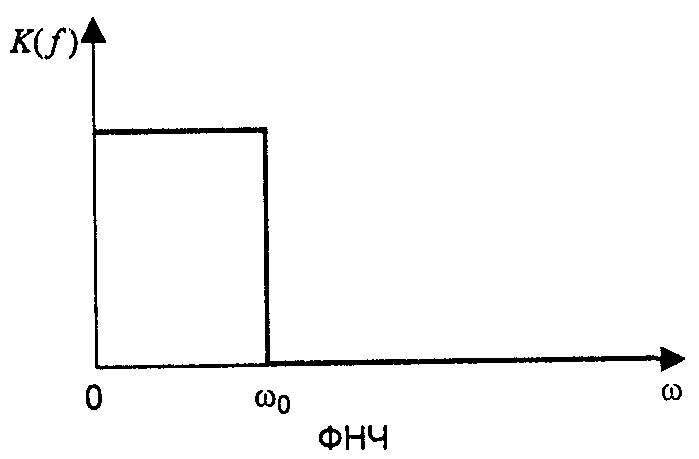
1) ФНЧ (фильтр низких частот)

Пропускает только низкие частоты

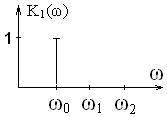
То есть K₁(ω) на ω₀ → 1, а на ω₁ и ω₂ → 0

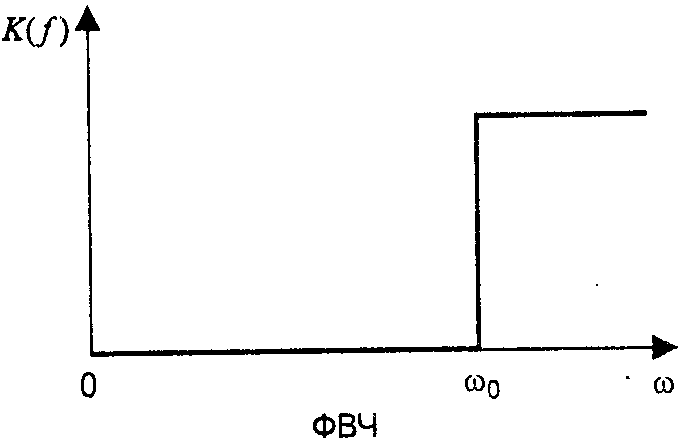
2) ФВЧ (верхних частот)

Пропускает только высокие частоты

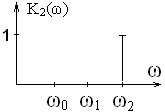
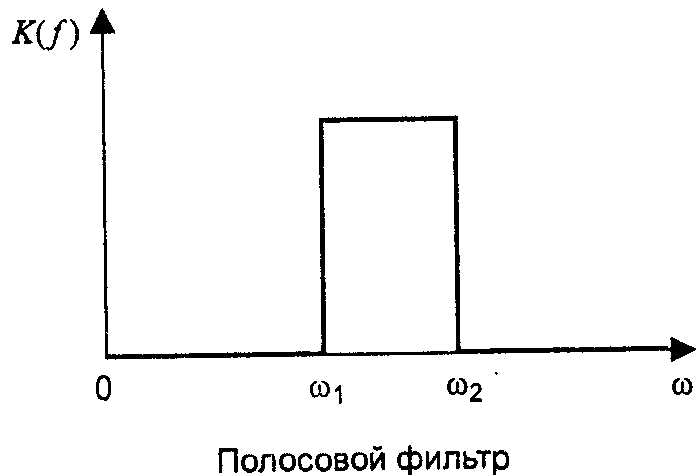
3) Полосовой фильтр

Пропускает частоты в некотором диапазоне

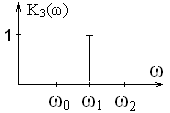
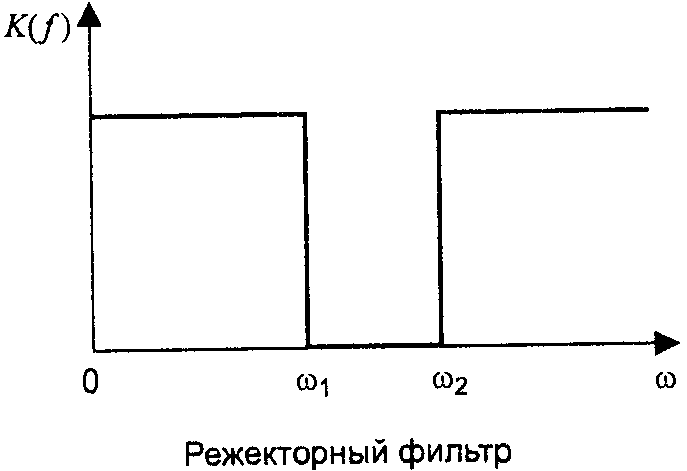
4) Режекторный фильтр

Пропускает все частоты кроме некоторого диапазона

Идеальная форма АЧХ таких фильтров:

Расчёт аналогового фильтра начинается с расчёта фильтра – прототипа, представляющего собой ФНЧ с частотой среза = 1 рад\с.

Далее рассматриваются различные фильтры – прототипы.

Фильтр Баттерворта

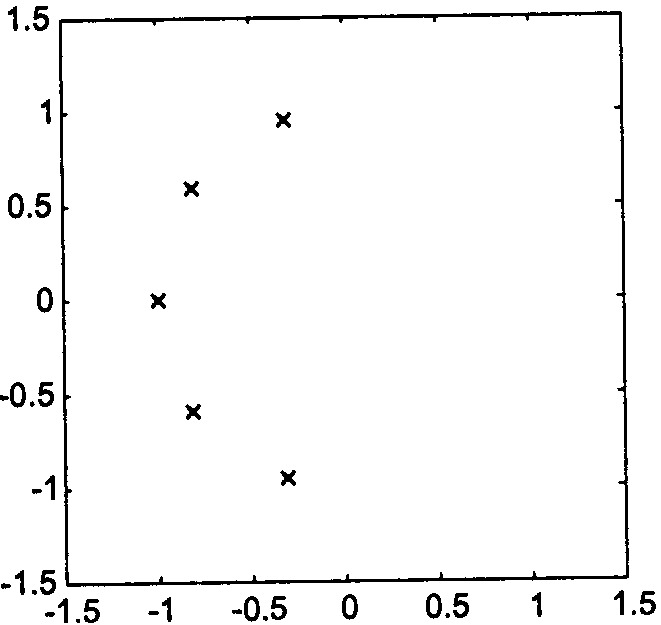
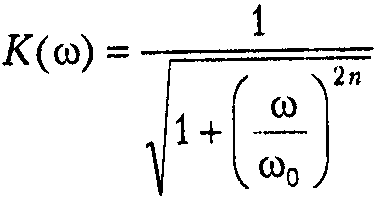Ф-ия передачи этого прототипа не имеет нулей, а её полюсы равномерно расположены на S-плоскости в левой половине окружности единичного радиуса.

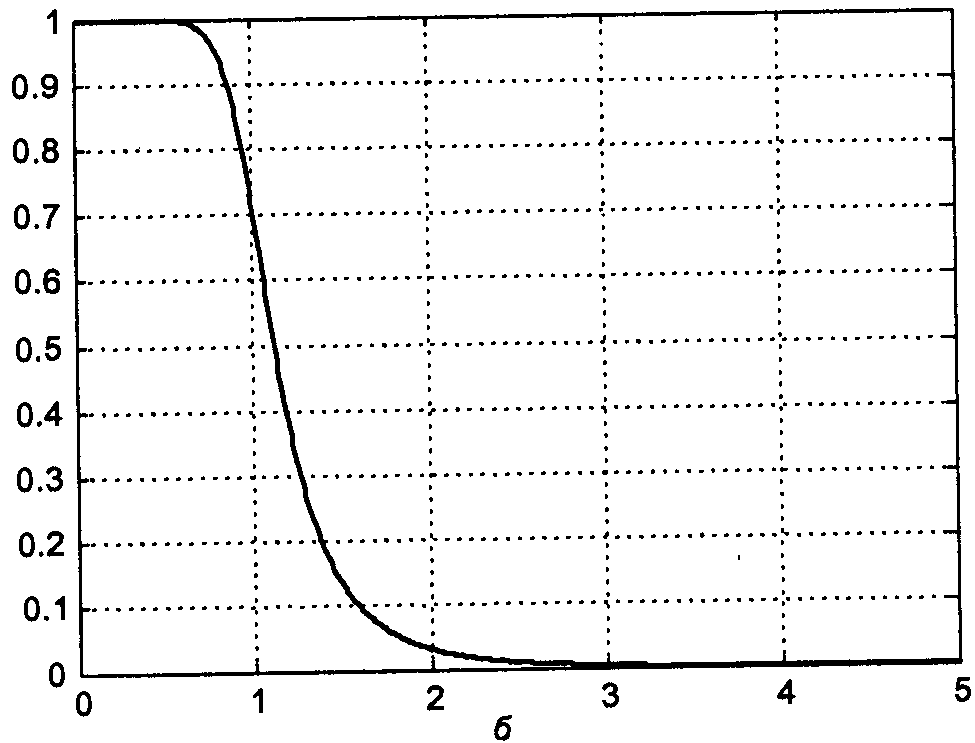
Формула для АЧХ фильтра Баттерворта:

ω₀ – частота среза

n – порядок фильтра

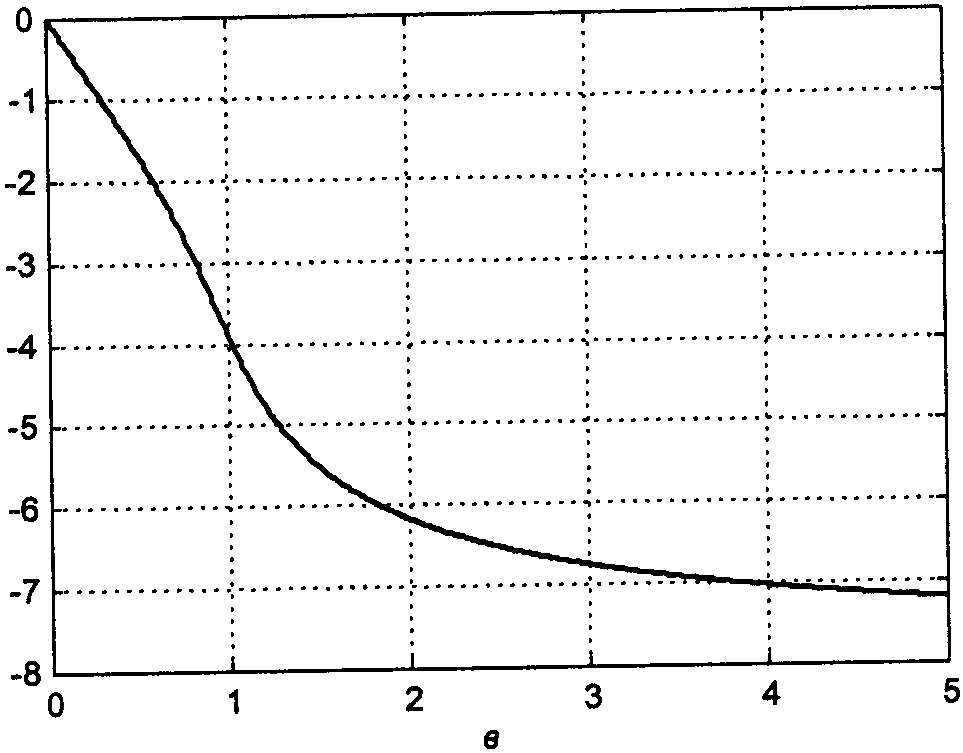
Фильтр Чебышева первого рода

А ЧХ фильтра:

ω₀ – частота среза; T_n(x) – полином Чебышева n-го порядка;

n – порядок фильтра; ε – параметр, определяющий величину пульсаций АЧХ в полосе пропускания.

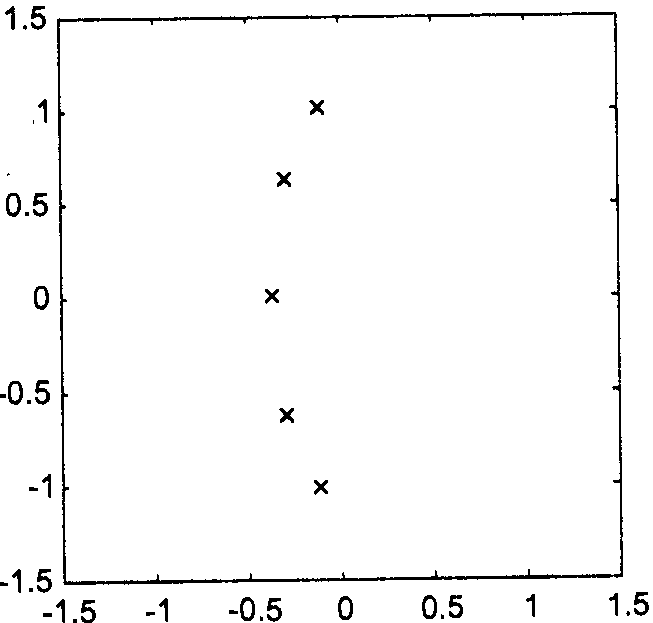
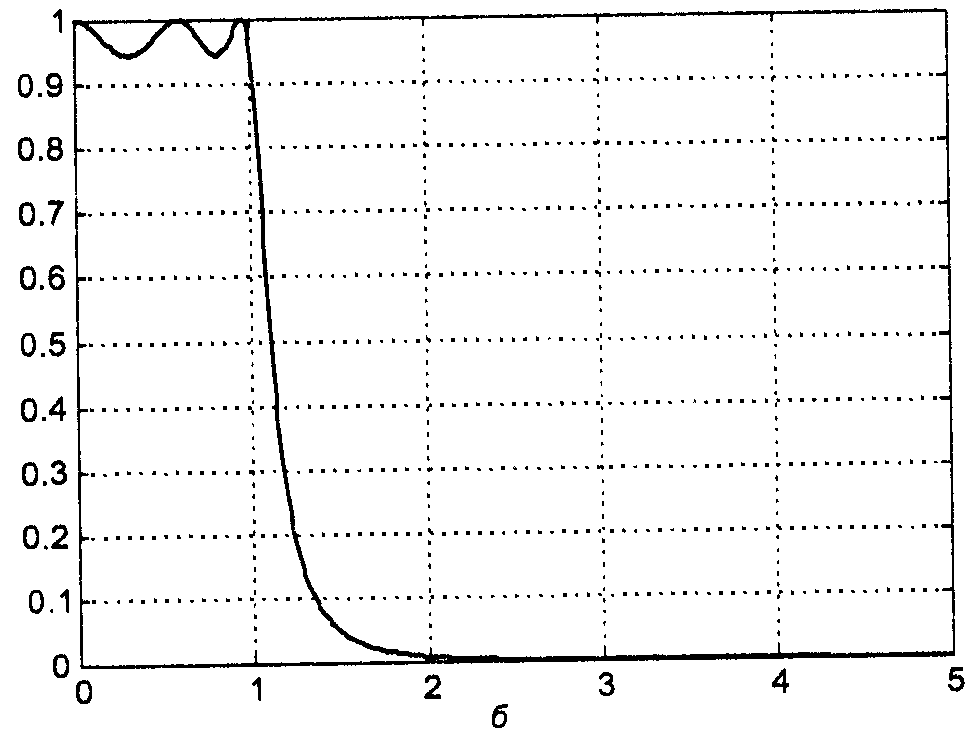
Полином Чебышева T_n(x) при |x|≤1 колеблется в диапазоне -1..+1., а при |x|>1 неограниченно возрастает.

П оэтому АЧХ в полосе пропускания (при |ω|≤ω₀ ) колеблется между значениями и 1, а вне полосы пропускания монотонно затухает до нуля.

По сравнению с фильтром Баттерворта того же порядка, фильтр Чебышева обеспечивает более крутой спад АЧХ в области перехода от полосы пропускания к полосе задерживания.

Значения параметра ε и уровень пульсаций R_p(в ДБ) связаны:
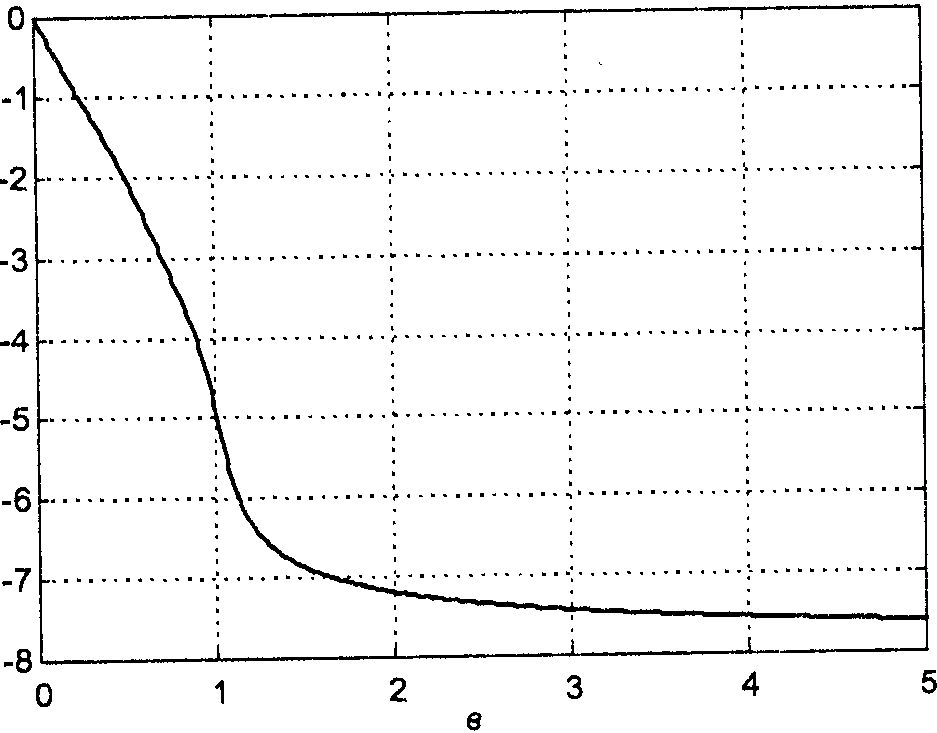