№1

Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом они представляются в виде суммы гармонич. функций с частотами, образующими арифм. прогрессию.

Для разложения необх. выполнение условий Дирихле (для фрагмента сигнала длительностью в один период):

• не должно быть разрывов 2 рода (с уходящими в бесконечность ветвями ф-ии)

• число разрывов 1 рода (скачков) должно быть конечным

• число экстремумов должно быть конечным

Синусно – косинусная форма записи ряда

, где

T – период повторения сигнала

Коэффициенты ряда рассчитываются по формулам:

Если сигнал S(t) - чётная функция, то все b_k=0, если нечётная, все a_k=0.

Вещественная форма записи ряда

Здесь исп-ся формула

Теперь

Комплексная форма записи

Используя ф-лу Эйлера , находим

. Подставим такой cos(x) в ряд, записанный в вещественной форме:

Компоненты со знаком «-» трактуем как члены ряда с отриц. номерами. Получим комплексную форму ряда:

, , ,

№2

Преобразование Фурье явл-ся инструментом спектрального анализа непериодических сигналов.

прямое преобразование Фурье

обратное преобразование Фурье

S(ω) – спектральная функция сигнала S(t)

Чтобы преобр-ие Фурье было применимо, сигнал S(t) должен отвечать требованиям:

• не должно быть разрывов 2 рода (с уходящими в бесконечность ветвями ф-ии)

• число разрывов 1 рода (скачков) должно быть конечным

• число экстремумов должно быть конечным

• 

Часто исп-ют не круговую частоту ω, а обычную f, тогда

прямое преобр-ие

обратное преобр-ие

Св-ва преобр-ия Фурье

Представим, что есть два абстрактных сигнала f(t), g(t), их спектральные ф-ии равны F(ω), G(ω).

1) Линейность

Если , то

Док-во:

2) Задержка

Если , то

3) Изменение масштаба времени

Если S(t)=f(at), то

4) Дифференцирование сигнала

(исп-сь 2 св-во и правило Лопиталя)

5) Интегрирование сигнала

, где δ(ω) это дельта - ф-ия

6) Свёртка сигналов

7) Произведение сигналов

S(t)=f(t)g(t),

№3

Для анализа св-в и хар-к случайного процесса необх-мо задать матем. модель случ. процесса. Эта модель предст-ет собой описание возможных реализаций случ. процесса в сочетании с указанием относит. частоты их появления.

Примеры моделей случ. процессов:

1) Гармонический сигнал со случ-ой нач. фазой

A и ω определены, а фаза φ явл-ся случайной, равномерно распределённой на интервале 0..2π, т.е. имеющую следующую плотность вероятности:

2) Случайный телеграфный сигнал

Это случ-ый процесс, реализации которого принимают значения +1 и -1, причём перепады уровня происходят в случ-ые моменты времени, и число перепадов уровня, происходящих за время τ, явл-ся случ-ой величиной с дискретным распред-ем вер-ти, описываемым законом Пуассона.

Вводные понятия:

Пусть X(t) – случ. процесс

Ф-ия распред-ия вер-ти равна вер-ти того, что в момент времени t1, знач-ие случ-го процесса не превосходит x:

Явл-ся неубывающ. ф-ей. ,

Одномерная плотность вер-ти

- вер-ть попадания случ. процесса X(t₁)в бесконечно малый интервал dx в окрестности x

Математическое ожидание – среднее значение случ. процесса в момент времени t

Дисперсия – средняя мощность отклонений случ. процесса от его среднего значения m_x(t)

Среднее квадратическое отклонение – мера разброса значений случ. процесса в момент времени t отн-но мат. ожидания

Законы распределения

Равномерное распределение

,

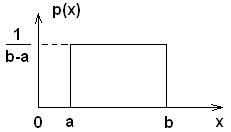
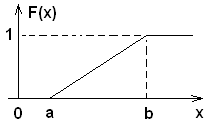
Нормальное распределение(по Гауссу)

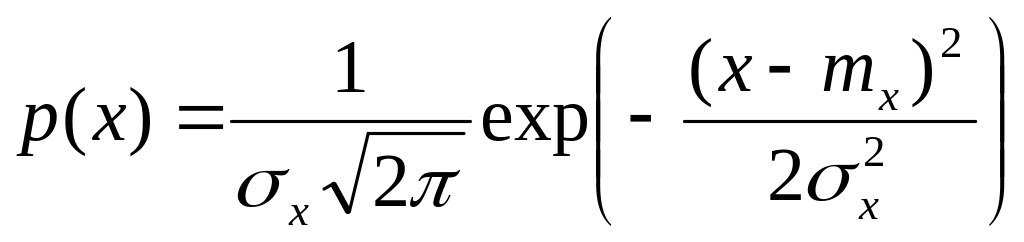
Для m_x=0, σ_x=1, плотность вер-ти

будет как на графике:

Вычисляется вспомогательный интеграл вероятности

Корреляционные ф-ии случайных процессов

- двумерная плотность вер-ти

- вер-ть того, что реализация случ. процесса X(t) в момент времени t₁ попадает в бесконечно малый интервал шириной dx₁, в окр-ти x_1, а в момент t₂ соотв-но в интервал dx₂ в окр-ти x₂

- ковариационная ф-ия случ. процесса.

=

=

это корреляционная ф-ия, она характ-ет степень статистической связи тех значений случ. процесса, кот. наблюдаются при t=t₁, и при t=t₂.

2 случайных процесса X₁ и X₂ независимы, если p(x₁,x₂)=p₁(x₁)p₂(x₂)

--------------------------------------------------------------------------------------------------

Для примера рассчитаем корреляционную ф-ию гармонич. сигнала со случайной равномерно распределённой фазой:

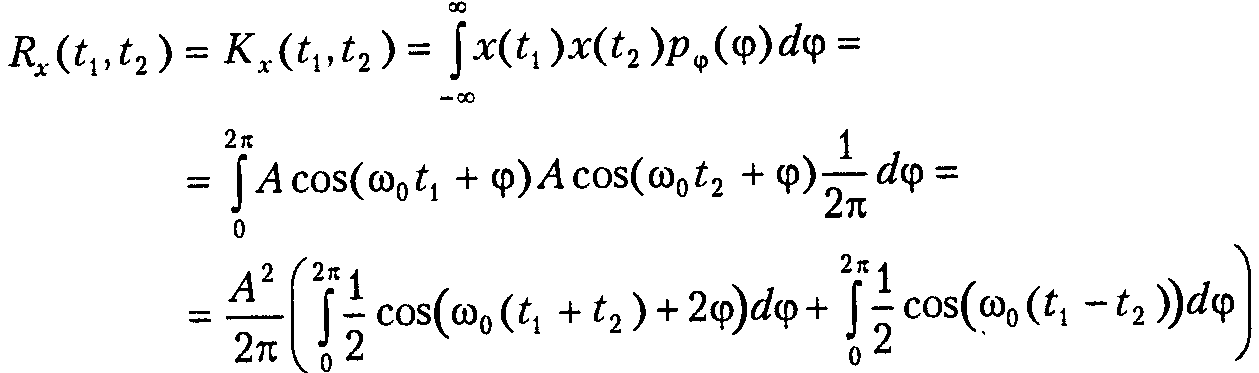
При первом слагаемом интегрир-ие производится по 2 периодам ф-ии cos, поэтому данный интеграл = 0. Во втором слаг-ом подынтегр-ая ф-ия не зависит от переменной интегрир-ия, поэтому:

--------------------------------------------------------------------------------------------------

Мерой линейной статистической связи между случайными величинами явл-ся коэфф-ет корреляции:

Значения +1 и -1 достигаются, если x₂=ax₁+b, т.е. 2 случ. процесса жёстко связаны линейно

Если r₁₂ = 0, между процессами корреляционной связи нет.

Стационарные случайные процессы

Это такие процессы, статистические хар-ки которых одинаковы во всех временных сечениях.

Случайный процесс строго стационарен (стационарен в узком смысле), если его многомерная плотность вер-ти произвольной размерности n не изменяется при одновременном сдвиге всех временных сечений вдоль оси времени на величину τ:

Если ограничить требование тем, чтобы от временного сдвига не зависели лишь одномерная и двумерная плотности вер-ти, то такой случ. процесс будет стационарен в широком смысле.

Для стационарного случ. процесса

m_x(t)=m_x=const; D_x(t)=D_x=const; т.е. не зависят от времени

А корреляционная ф-ия зависит только от интервала τ:

Корреляционная ф-ия стацион. случ. процесса явл-ся чётной.

Часто удобно бывает использовать коэфф-ет корреляции:

----------------------------------------------------------------------------------------------

Пример из раздела «Корреляционные ф-ии случайных процессов» явл-ся стационарным в широком смысле. Потому что зависящие от одномерной плотности вер-ти мат. ожидание и дисперсия не зависят от времени, а корреляционная ф-ия, зависящая от двумерной плотности вер-ти, зависит лишь от интервала между рассматриваемыми моментами времени:

----------------------------------------------------------------------------------------------