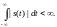3.2.3. Интеграл Фурье
Интеграл Фурье. Спектры непериодических сигналов конечной длительности (финитных), заданных на интервале Т, могут быть получены из уравнений для рядов Фурье как предельные значения функций при расширении периода Т до бесконечности. При этом дискретные частоты nΔω обращаются в непрерывные текущие значения ω, а суммирование амплитудных значений в (3.2.1) заменятся интегрированием:
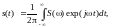(3.2.7)
. (3.2.8)
На рис. 3.2.5 сплошной кривой приведен пример непрерывного сигнала s(t), энергия которого сосредоточена на конечном интервале T = (0,25).
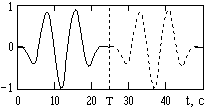
Рис. 3.2.5. Периодическое повторение сигнала
Если нас не интересует форма данного сигнала за пределами интервала Т, то спектр сигнала в виде ряда Фурье можно определить по формуле (3.2.2). При обратном преобразовании Фурье по формуле (3.2.1), т.е. при восстановлении сигнала по его спектру, в интервале Т будет восстановлен исходный сигнал s(t). Но если интервал для восстановления будет задан больше интервала Т, например (0, 2Т), то за пределами этого интервала начнется периодическое повторение исходного сигнала, как это показано пунктиром на Рис. 3.2.5. Если такой процесс нежелателен и за пределами интервала Т должны быть сохранены нулевые значения сигнала, необходимо использовать интегральное преобразование Фурье (3.2.7-8).
Спектральная функция S(ω) представляет собой не спектр, а комплексную спектральную плотность сигнала, непрерывную на частотном интервале от - до . Она содержит четную действительную и нечетную мнимую части:
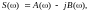(3.2.9)
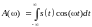, (3.2.10)
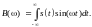(3.2.11)
Пример спектральной функции S(f) для сигнала s(t) на Рис. 3.2.5 приведен на Рис. 3.2.6. Графическое изображение спектральных функций выполняется в виде модуля и аргумента функции, приведенных на рис. 3.2.7. Такое представление аналогично (3.2.3'):
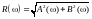, (3.2.12)
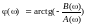. (3.2.13)
Еще раз подчеркнем
различие между спектрами и спектральными
функциями сигналов. При практическом
использовании формулы (3.2.8) для вычисления
спектральных функций конечных сигналов,
заданных на определенном интервале Т,
пределы интегрирования обычно
устанавливаются по границам интервала
Т,
так как нет необходимости выполнять
интегрирование в бесконечных пределах,
если за пределами интервала Т мы имеем
нулевые (или незначимые) значения
сигнала. Однако при сравнении формулы
(3.2.8) с выражением (3.2.2) можно видеть, что
значения интеграла (3.2.8) не нормируются
на величину интервала Т.
Отсюда следует, что прямые числовые
отсчеты значений модуля функции S(ω)
для определенных значений ωi
не являются амплитудными значениями
соответствующих гармонических колебаний
с частотой ωi.
Значения S(ω)
по сравнению со значениями функции
S(nΔω)
по (3.2.2) при nΔω
= ωi
завышены на множитель Т.
Это можно объяснить тем, что обратное
преобразование Фурье по (3.2.1) представляет
собой прямое суммирование гармоник с
соответствующими амплитудами колебаний,
в то время как интегрирование по (3.2.7)
представляет собой предельное суммирование
значений S(ωi)dωi,
где
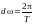при →
.
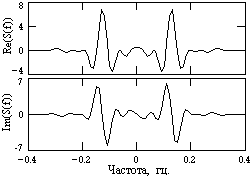
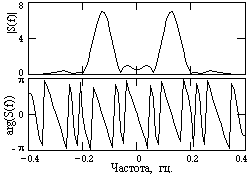
Рис. 3.2.6. Рис. 3.1.7.
Тригонометрическая форма интеграла Фурье:
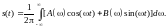(3.2.14)
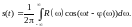(3.2.14')
Пары выражений (3.2.1-2) и (3.2.7-8) называют прямым и обратным преобразованием Фурье. Этими выражениями устанавливается взаимно однозначная связь сигнала и его спектра (спектральной плотности). Прямое и обратное преобразование Фурье подобны и любая теорема, доказанная для одного из них, справедлива и для другого. Особенно наглядно (см. Рис. 3.2.8) это видно для четных сигналов, для которых В(ω) = 0 и фазовый спектр равен нулю:
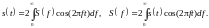
Для упрощения записей используют и другое обозначение преобразования Фурье:
s(t) ↔ S(f), s(t) ↔ S(ω),
где, в общем случае, как сама функция, так и ее Фурье-образ могут быть комплексными.
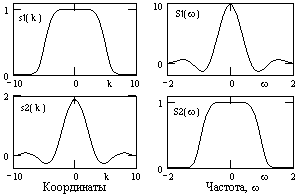
Рис. 3.2.8.
Для физических сигналов преобразование Фурье, как правило, всегда существует. Сигналу s(t) можно сопоставить спектральную плотность S(ω), если существует интеграл:
