3.2.2. Ряд Фурье

Ряд Фурье. Периодическую функцию любой формы, заданную на интервале одного периода Т = b - a и удовлетворяющую на этом интервале условиям Дирехле (ограниченная, кусочно-непрерывная, с конечным числом разрывов 1 рода), можно представить в виде ряда Фурье:

(3.2.1)

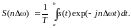(3.2.2)

Ряд Фурье представляет собой ансамбль единичных гармонических функций 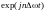с весовыми коэффициентами 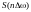, на которые можно разложить периодический сигнал s(t). Функцию весовых коэффициентов принято называть комплексным спектром периодического сигнала или Фурье-образом функции s(t). Спектр периодического сигнала дискретен, т.к. функция определена только для целых значений n с шагом по частоте, обратным периоду: 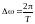(или ). Значения по положительным и отрицательным значениям n являются комплексно сопряженными.

Подынтегральную функцию экспоненты в выражении (3.2.2) можно разложить на составляющие и выразить комплексный спектр в виде действительной и мнимой части:

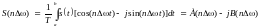, (3.2.3)

(3.2.4)

(3.2.5)

На Рис. 3.2.1 приведен пример периодического сигнала (треугольный импульс на интервале (3 - 5), повторяющийся с периодом Т = 40) и форма действительной и мнимой части его спектра. Действительная часть спектра является четной относительно нуля функцие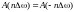й , а мнимая часть спектра - нечетной функцией .

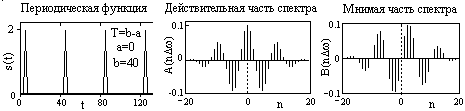
Рис. 3.2.1. Сигнал и его комплексный спектр

Другая форма записи комплексного спектра:

, (3.2.3')

Модуль спектра называют двусторонним спектром амплитуд, а аргумент спектра, последовательность фазовых углов - двусторонним спектром фаз. Спектр амплитуд представляет собой четную функцию: , а спектр фаз нечетную: . Пример спектров, альтернативных представлению на Рис. 3.2.1, приведен на Рис. 3.2.2.

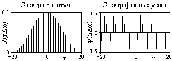
Рис. 3.2.2. Модуль и аргумент комплексного спектра

При n = 0 имеем В₀ = 0 и получаем постоянную составляющую сигнала:

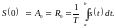
Первую частотную составляющую спектра при n = 1, ω₁ =1, (или 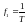), называют основной частотой сигнала (первой гармоникой), остальные частоты дискретного спектра nω₁ при n > 1 - гармониками сигнала.

Тригонометрическая форма. Объединяя в (3.2.1) комплексно сопряженные составляющие, можно перейти к ряду Фурье в тригонометрической форме:

(3.2.6)

(3.2.6')

Ряд (3.2.6) представляют собой разложение периодического сигнала s(t) на сумму некомплексных элементарных гармонических функций (косинусных и синусных) с весовыми коэффициентами, удвоенные значения которых (т.е. значения 2A_n, 2B_n) не что иное, как амплитуды соответствующих гармонических колебаний. Совокупность амплитудных значений этих гармоник образует односторонний физически реальный (только для положительных частот nΔω) спектр сигнала, приведенный на рис. 3.2.3 (спектр треугольного сигнала рис. 3.2.1). Но такое графическое отображение спектра используется довольно редко.

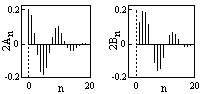
Рис. 3.2.3. Спектр амплитуд косинусных и синусных гармоник

Более широкое применение для отображения односторонних физически реальных спектров находит формула (3.2.6'). Спектр амплитуд при таком отображении называется амплитудно-частотной характеристикой сигнала (АЧХ), а спектр фазовых углов – фазо-частотной характеристикой (ФЧХ). Пример спектра (треугольного сигнала на Рис. 3.2.1) приведен на Рис. 3.2.4.

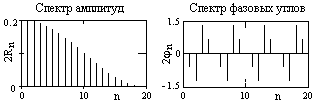
Рис. 3.2.4. АЧХ и ФЧХ треугольного сигнала

Ряды Фурье произвольных аналоговых периодических сигналов могут содержать бесконечное число членов. Однако одним из важных достоинств преобразования Фурье является то, что при ограничении (усечении) ряда Фурье до любого конечного числа его членов обеспечивается наилучшее (для данного количества членов) среднеквадратическое приближение к исходной функции.

Аналогично в ряд Фурье может разлагаться и произвольная конечная (непериодическая) функция, заданная на интервале (a, b), что автоматически означает ее периодическое продолжение за пределами заданного интервала (в обе стороны от него) с периодом Т = b - a.