
- •3. Временное и частотное представление сигналов
- •3.1. Временное представление сигналов
- •3.1.1. Разложение сигналов по единичным импульсам
- •3.1.2. Свертка (конволюция)
- •3.2. Частотное представление сигналов
- •3.2.1. Разложение сигналов по гармоническим функциям
- •3.2.2. Ряд Фурье
- •3.2.3. Интеграл Фурье
3.1.2. Свертка (конволюция)
Интеграл Дюамеля. Произвольный сигнал на входе системы с использованием выражений разложения сигнала может быть представлен в виде последовательной линейной комбинации взвешенных единичных импульсов:
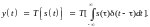
На основании принципа суперпозиции линейный оператор Т может быть внесен под знак интеграла, т.к. последний представляет собой предельное значение суммы. При этом операция преобразования действует только по переменной t. Отсюда следует:
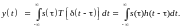
Это выражение представляет собой интеграл Дюамеля или свертку (конволюцию) входного сигнала с импульсной характеристикой системы. Заменой переменных t - = можно убедиться в том, что свертка коммутативна:
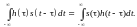
Приведенные выше выражения имеют специальную форму упрощенной математической записи в символическом виде:
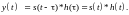
Аналогично, для дискретных сигналов:
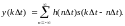
Свойства свертки. Для свертки характерны следующие свойства:
1. Дистрибутивность:
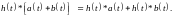
2. Коммутативность:
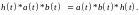
3. Aссоциативность:
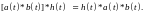
Преобразование свертки однозначно определяет выходной сигнал y(t) для входного сигнала s(t) при известном значении функции импульсного отклика системы h(t). Обратная задача деконволюции - определение функции s(t) по функциям y(t) и h(t), относится к разряду некорректных потому, что свертка может изменить частотный спектр сигнала y(t) и восстановление функции s(t) становится невозможным.
Любая практическая система должна быть устойчивой, т.е. для сигналов, конечных по энергии или средней мощности, выходные сигналы также должны быть конечными по этим параметрам. Устойчивость обеспечивается при выполнении условия абсолютной интегрируемости импульсного отклика системы:
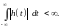
3.2. Частотное представление сигналов
3.2.1. Разложение сигналов по гармоническим функциям
Частотная
(спектральная) форма представления
сигналов использует разложение сигнальных
функций на гармонические составляющие.
В качестве базисных функций разложения
в общем случае принимаются комплексные
экспоненциальные функции exp(jft),
от которых с использованием формул
Эйлера всегда можно перейти к
синус-косинусным функциям. Термин
«частотная» обязан своим происхождением
независимой переменной данного
представления сигналов, которая
измеряется в единицах частоты (Гц),
обратных единицам времени
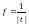 .
В математическом аппарате частотного
анализа используют угловую частоту =
2f,
измеряемую в радианах.
.
В математическом аппарате частотного
анализа используют угловую частоту =
2f,
измеряемую в радианах.
Понятие собственных функций. Удобство использования частотного представления сигналов заключается в том, что гармонические функции являются собственными функциями операций переноса, интегрирования, дифференцирования и других линейных операций, инвариантных во времени.
Пусть исходная функция является линейной комбинацией функций:
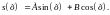
Осуществим произвольный сдвиг функции по аргументу на величину h. Получаем:
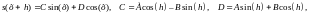
где коэффициенты C и D, как и в исходном выражении коэффициенты А и В, не зависят от аргумента, при этом C2 + D2 = А2 + В2. Таким образом, при произвольном переносе функции по аргументу (при любых линейных преобразованиях) линейную комбинацию синуса и косинуса можно представить линейной комбинацией этих же функций.
Экспоненциальная комплексная запись гармонических функций делает это свойство еще нагляднее. Для произвольной гармонической функции имеем:
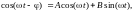
где A = cos(φ), B = sin(φ), φ- начальный фазовый угол колебания при t = 0. Переходя к комплексной записи данной функции с использованием тождеств Эйлера
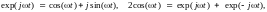
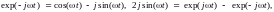
получаем:
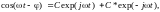
где:
C
= 0.5exp(-j),
C*
= 0.5exp(j)
- комплексно сопряженная с С
величина. Применяя в качестве гармонической
составляющей разложения сигнала
комплексную функцию
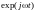 ,
можно рассматривать вторую функцию
,
можно рассматривать вторую функцию
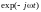 ,
комплексно сопряженную с первой, как
такую же составляющую, но с отрицательной
частотой. Естественно, что отрицательная
частота является чисто математической
абстракцией, но нужно помнить, что пара
таких комплексно сопряженных составляющих
в сумме всегда дает вещественную функцию.
,
комплексно сопряженную с первой, как
такую же составляющую, но с отрицательной
частотой. Естественно, что отрицательная
частота является чисто математической
абстракцией, но нужно помнить, что пара
таких комплексно сопряженных составляющих
в сумме всегда дает вещественную функцию.
Экспоненциальные функции также являются собственными функциями линейных операций. Для операции переноса с использованием экспоненциальных функций:
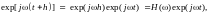
где Н() = exp(jh) - собственное значение операции переноса, независимое от переменной.
Для операции дифференцирования:
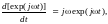 H()
= j.
H()
= j.
Для операции интегрирования:
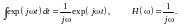
В общем виде для любых линейных операций:
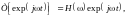
где
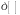 -
линейный оператор, H()
- собственное значение операции,
независимое от t.
-
линейный оператор, H()
- собственное значение операции,
независимое от t.
