Принятый план поставок тары на заводы по производству рохладительных напитков

Поставщики	Количество поставляемых бутылок.
	А	Б
В	4500	3000
Г	500	500

3.2.3. Разработка рекомендаций по логистизации поставок сырья для предприятий одного экономического района

Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 120, 50, 190 и 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы поставок являются известными величинами и задаются матрицей

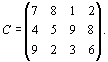
Составить такой план поставок, при котором их общая стоимость является минимальной.

4. Диагностика и решение логистических проблем планирования замены оборудования на предприятии

4.1. Методика выявления и решения логистической проблемы планирования замены оборудования

А). Исходные данные

В связи с физическим и моральным устареванием оборудования на предприятии требуется его замена. Логистическая проблема заключается в том, чтобы разработать такой план замены оборудования, при котором стоимость замены была бы минимальной. Для решения этой задачи используется метод критического пути.

Пусть задана транспортная сеть (рис 4.1), состоящая из станций А0, А1 и т.д. и коммуникаций, соединяющих некоторые из этих станций.

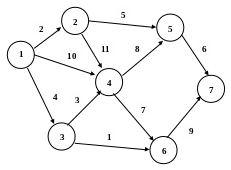
Рис. 4.1 Транспортная сеть

Длины коммуникаций предполагаются известными и равными C_ij. Если станции А_i и А_j непосредственно не соединены друг с другом, предполагаем что С_ij равна бесконечности. Из начальной станции А₀ на конечную станцию А_n+1 можно попасть через большое количество путей, проходящих через разные промежуточные станции. Требуется выделить из всех путей путь наименьшей длины. Поясним, что применительно к замене оборудования станции рассматриваются как номера периодов замены, а длины коммуникаций, как стоимости замены.

Б). Экономико-математическая модель решения задачи

Приведем в соответствии каждой паре пунктов А_i и А_j величины Х_ij.

Если участок А_iА_j принадлежит кратчайшему пути Х_ij=1 и, Х_ij =0 в противном случае. Задача о кратчайшем пути в таком случае может быть сведена к выбору чисел Х_ij, для которых сумма произведений длины дуг на искомые переменные Х_ij стремится к минимуму при условиях:

(4.1)

(4.2)

(4.3)

(4.4)

(4.5)

Условие 4.2 соответствует тому, что число коммуникаций, принадлежащих критическому пути и в ходящих в любой промежуточный пункт равно числу коммуникаций исходящих из этого пункта и принадлежащих критическому пути.

Условие 4.3 означает, что количество коммуникаций из исходного пункта А₀ превышает на единицу число коммуникаций входящих в исходный пункт.

Аналогичным образом условие 4.4 свидетельствует о том, что в конечный пункт А_n+1 входит на одну коммуникацию больше, чем выходит.

Вместе с условием 4.2 и требованием минимизации целевой функции 4.1 условия 4.3 и 4.4 означают, что на каждую станцию А_i приходит ровно одна коммуникация и из каждой станции А_i исходит ровно одна коммуникация.

Условие 4.5 в задаче эквивалентно требованию, согласно которому все значения Х_ij равны нулю или единице.

Таким образом, соотношения 4.1-4.5 определяет кратчайший путь в сети. Необходимо еще раз отметить, что в качестве длин дуг могут быть не только километры, но и другие показатели, например стоимости, время и т.д. Транспортная интерпретация дается здесь лишь только для того, что она наиболее понятна всем для восприятия.

В). Решение задачи по определению кратчайшего пути

Подготовительный этап

1). Преобразуем граф сети к матричной форме

С этой целью строим 2 таблицы – «Дуги» и «Узлы» (рис. 4.1).

В таблице «Дуги» выделяем 4 столбца:

1 столбец – «дуга», предназначен для заполнения значениями искомых переменных Х_ij.

2 столбец – «начало», обозначает исходные и промежуточные узлы сети, из которых выходят коммуникации (например, из узла 1 выходят 3 коммуникации).

3 столбец – «конец», предназначен для обозначения узлов промежуточных и конечных пунктов или станций, в которые входят коммуникации.

4 столбец – «длина», предназначен для указания протяженности дуг, соединяющих узлы друг с другом.

В таблице Узлы:

1 столбец – «узел», в нем размещается информация о номерах всех узлов, последовательно от исходного пункта до пункта стока или конечного пункта.

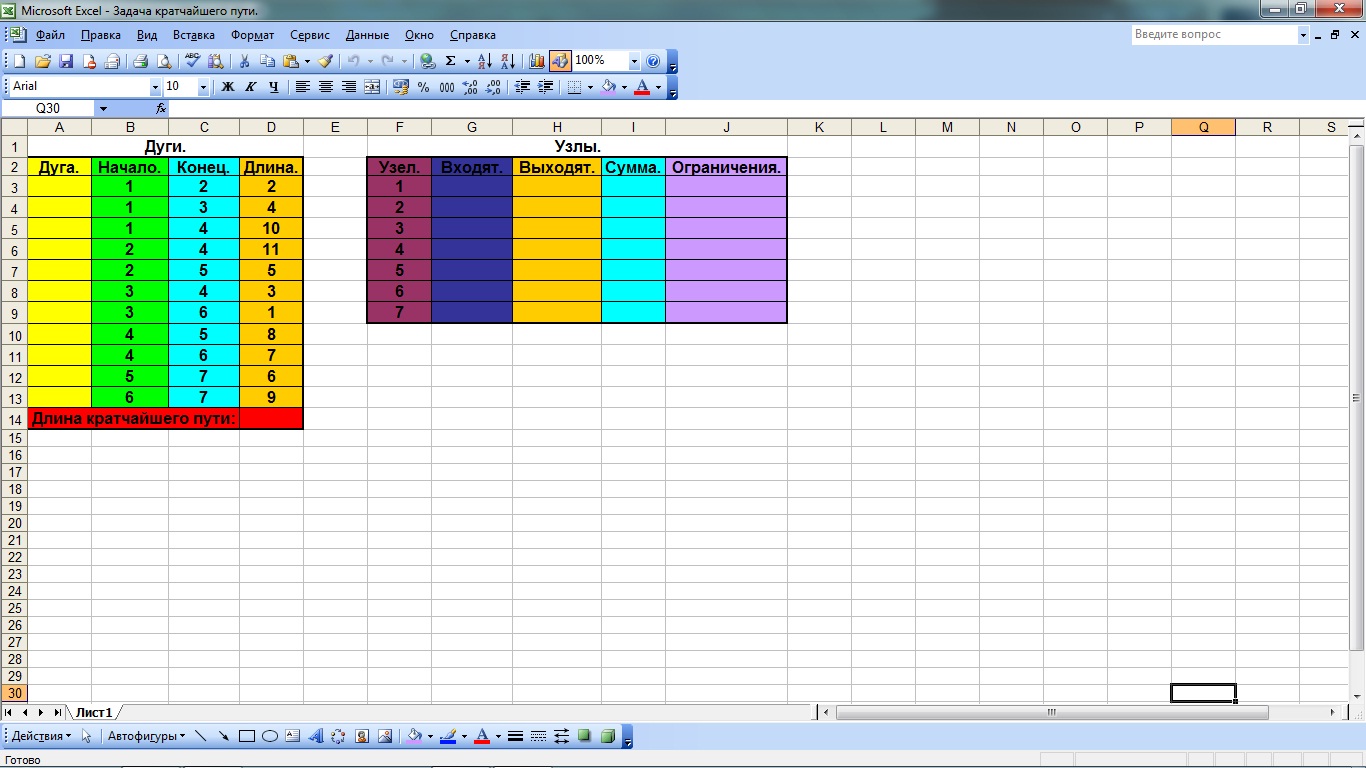
Рис. 4.1 Исходные таблицы «дуги» и «узлы»

2 столбец – «входят», заполняется автоматически в процессе решения задачи. Алгоритм решения основан на выборе кратчайшего расстояния до следующего узла с учетом суммы расстояний до предыдущего узла и длины коммуникаций до узла, следующего за предыдущим.

Тоже самое относится и к 3 столбцу – «выходят».

4 столбец – «сумма», предназначен для расчета значений ограничений.

5 столбец – ограничение – предназначен для обозначения исходного, конечного и промежуточных пунктов. Соответствующему номеру узла присваивается значение, 1 - если этот узел является исходным пунктом, 0 - если узел является промежуточным пунктом и -1 - если узел является конечным пунктом (условия 4.2,4.3,4.4).

2). Заполняем формулами таблицу «Дуги» для вычисления длины кратчайшего пути. С этой целью:

• выделяем ячейку, в которой мы хотим разместить значения длины кратчайшего пути, а затем вызываем «мастер функций» нажав на иконку fx на панели инструментов. В открывшемся окне в категории математические выбираем функцию СУММПРОИЗВ (рис. 4.2);

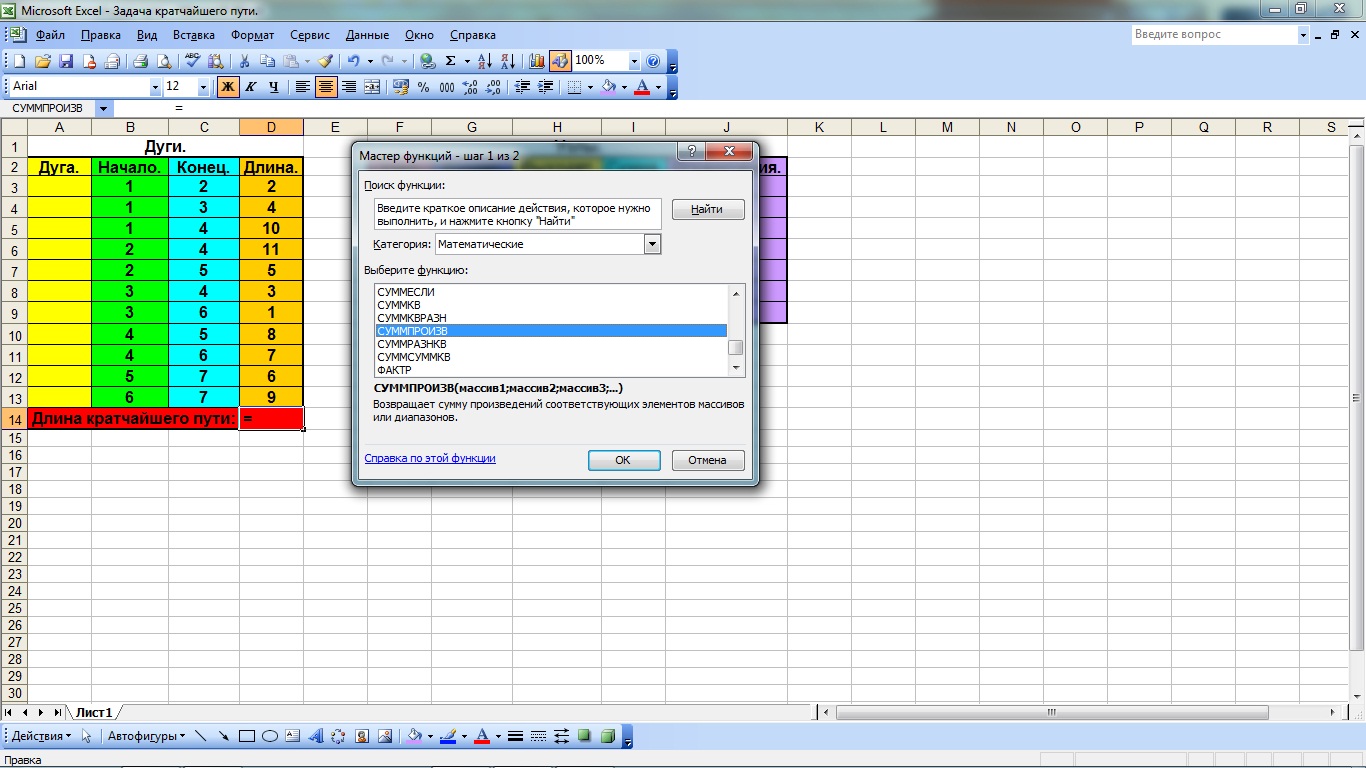
Рис. 4.2 Работа в окне «Мастер функций»

• в строку Массив 1 (рис. 4.3) вводим значения длин дуг, выделив столбец «длина» в таблице «дуги»;

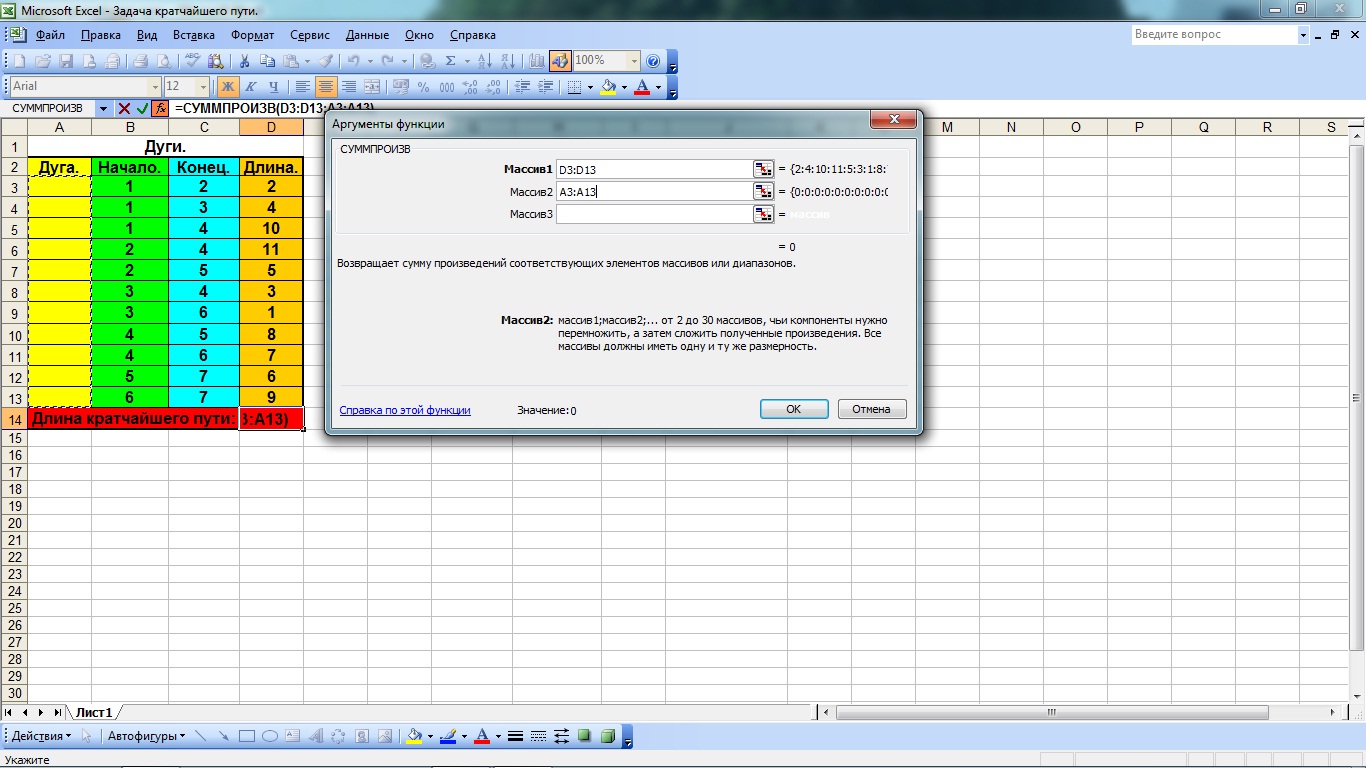
Рис. 4.3 Ввод аргументов функции СУММПРОИЗВ

• устанавливаем курсор в строку «массив 2» в окне Аргументы функции и вводим значения столбца – «Дуга» из таблицы «Дуги» и нажимаем ОК.

На этом ввод формул для таблицы Дуги закончен.

2). Заполняем формулами таблицу «Узлы». С этой целью:

• для расчета значений в столбце «Входят», устанавливаем курсор в ячейку на пересечении соответствующего узла 1 и столбца «Входят» и активируем ее, щелкнув левую кнопку мыши;

• вызываем мастер функций и в категории «математические» выбираем функцию «СУММЕСЛИ»;

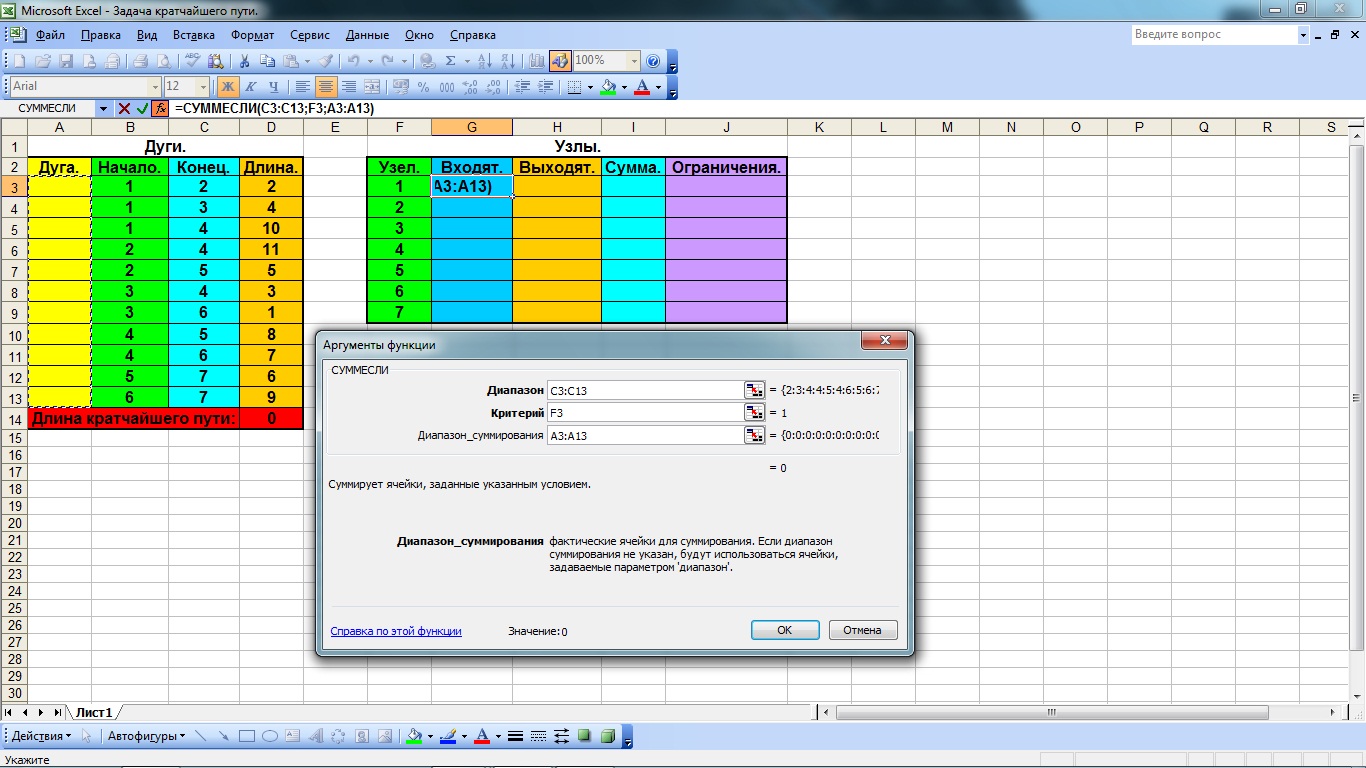
Рис. 4.4 Заполнение аргументов функции «СУММЕСЛИ»

• заполняем строку «Диапазон» в аргументах функции для чего вводим в эту строку значение массива конец из таблицы «Дуги»;

• переводим курсор в строку «критерии» в окне «Аргументы функции» и вводим значение, соответствующее номеру узла в строке таблицы «Узлы» (в нашем случае это значение ячейки F3;

• устанавливаем курсор в строку «диапазон суммирования» и вводим значения столбца «Дуга» (А3:А13) из таблицы «Дуги» (рис. 4.4);

• нажимаем ОК и переходим к вводу формулы «СУММЕСЛИ» в столбце входят следующего второго узла, при этом Аргументы функции, за исключением критерия, остаются прежними, а критерий соответствует следующему номеру узла. Аналогично вводим формулу для всех оставшихся узлов в столбце «Входят».

Переходим к заполнению формулами столбца «Выходят», для чего:

• устанавливаем курсор и выделяем ячейку на пересечении строки, соответствующей узлу 1 и столбцу «Выходят»;

• вызываем мастер функций и в категории математические выбираем функцию «СУММЕСЛИ»;

• в появившемся окне «Аргументы функции» устанавливаем курсор в строку диапазон и вводим значения столбца (массива) «Начало» из таблицы «Дуги»;

• устанавливаем курсор в строку «Критерий» в окне «Аргументы функции» и вводим значение критерия, которое соответствует значению номера узла 1 из таблицы «Узлы»;

• устанавливаем курсор в «Диапазон суммирования» в окне «Аргументы функции» и вводим значение диапазона суммирования, соответствующее значениям столбца «Дуга» из таблицы «Дуги». Нажимаем ОК. Аналогично вводим формулы в оставшиеся ячейки столбца «Выходят». При этом все аргументы функции, за исключением критерия, остаются прежними. Меняется лишь численное значение критерия, которое соответствует номеру следующего узла (рис. 4.5).

Рис. 4.5 Ввод формул в столбец «Выходят»

Переходим к заполнению формулами столбца «сумма». С этой целью:

• выделяем ячейку на пересечении строки, соответствующей узлу 1 и столбцу «Сумма». Нажимаем знак «=», устанавливаем курсор в этой же строке в столбце «Выходят» и нажимаем знак «минус»

• устанавливаем курсор в этой же строке в столбце «Входят», нажимаем «ENTER» (рис. 5.6).

• копируем формулу в остальные ячейки столбца «Сумма». Для этого выделяем ячейку, в которую мы только что вводили формулу и нажимаем «Копировать» на панели инструментов. Затем выделяем остальные ячейки в столбце «Сумма» и нажимаем «Вставить» на панели инструментов.

Далее заполняем данными столбец «Ограничения» (рис. 4.7). При этом в ячейке на пересечении столбца «Сумма» и строки, соответствующей каждому узлу, проставляем значение 1, если этот узел является исходным пунктом, значение 0, если узел является промежуточным и -1, если пункт будет конечным узлом (стоком).

На этом ввод формул в таблицу «Узлы» считается завершенным.

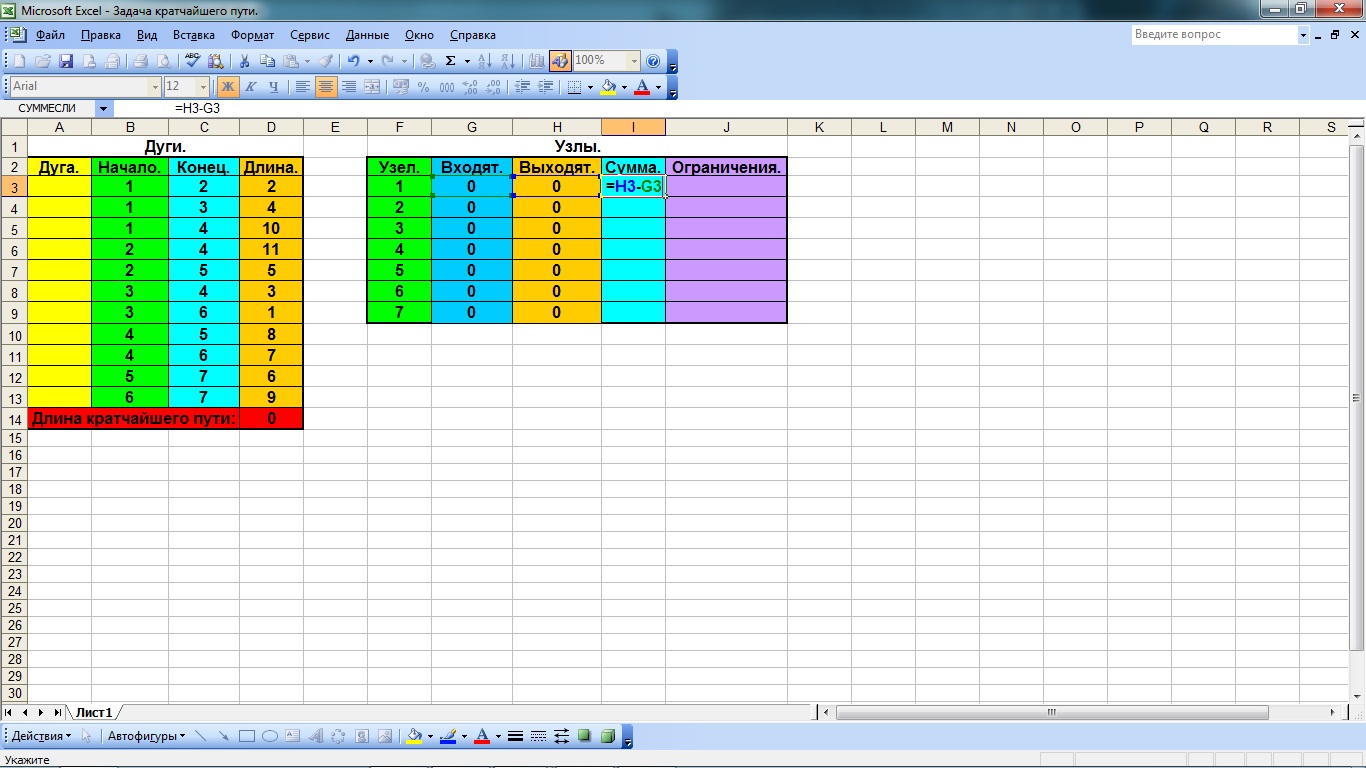
Рис. 4.6 Ввод формул в столбец «Сумма»

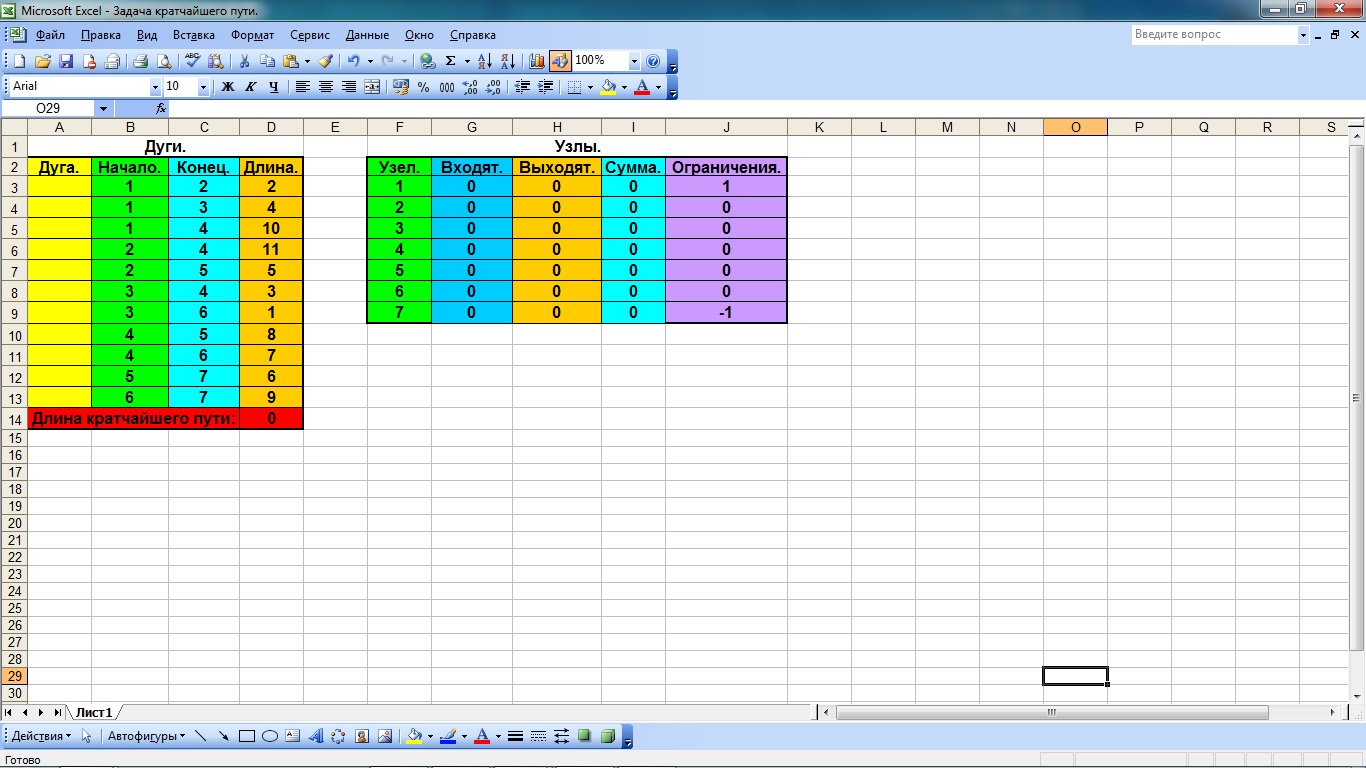
Рис. 4.7 Ввод данных в столбец «Ограничения»

Вычислительный этап

1). Устанавливаем курсор в ячейку, в которую будет помещено значение кратчайшего пути.

2). Запускаем программу «Поиск решения» командой Данные/ Анализ/ Поиск решения (Excel 2007) или Сервис/Поиск решения (Excel 2003 и ниже).⁶

3). В окне поиск решения (рис. 4.8) устанавливаем целевую ячейку, соответствующую номеру ячейки, в которой будет помещена длина кратчайшего пути.

4). Выбираем равенство этой ячейки минимальному значению и устанавливаем курсор в строку «изменяя ячейки».

5). Вводим в строку «изменяя ячейки» столбец (массив) «Дуга» из таблицы «Дуги».

Рис. 4.8 Работа в окне «Поиск решения»

5) Устанавливаем курсор в окно «Ограничения» и справа от этого окна нажимаем кнопку «Добавить» (Рис. 4.8).

6). В окно «Ссылка на ячейку» (рис. 4.9) вводим значения столбца «Сумма» из таблицы «Узлы».

7). В следующем окне (справа) выбираем знак «<=» и устанавливаем курсор в окно «Ограничения».

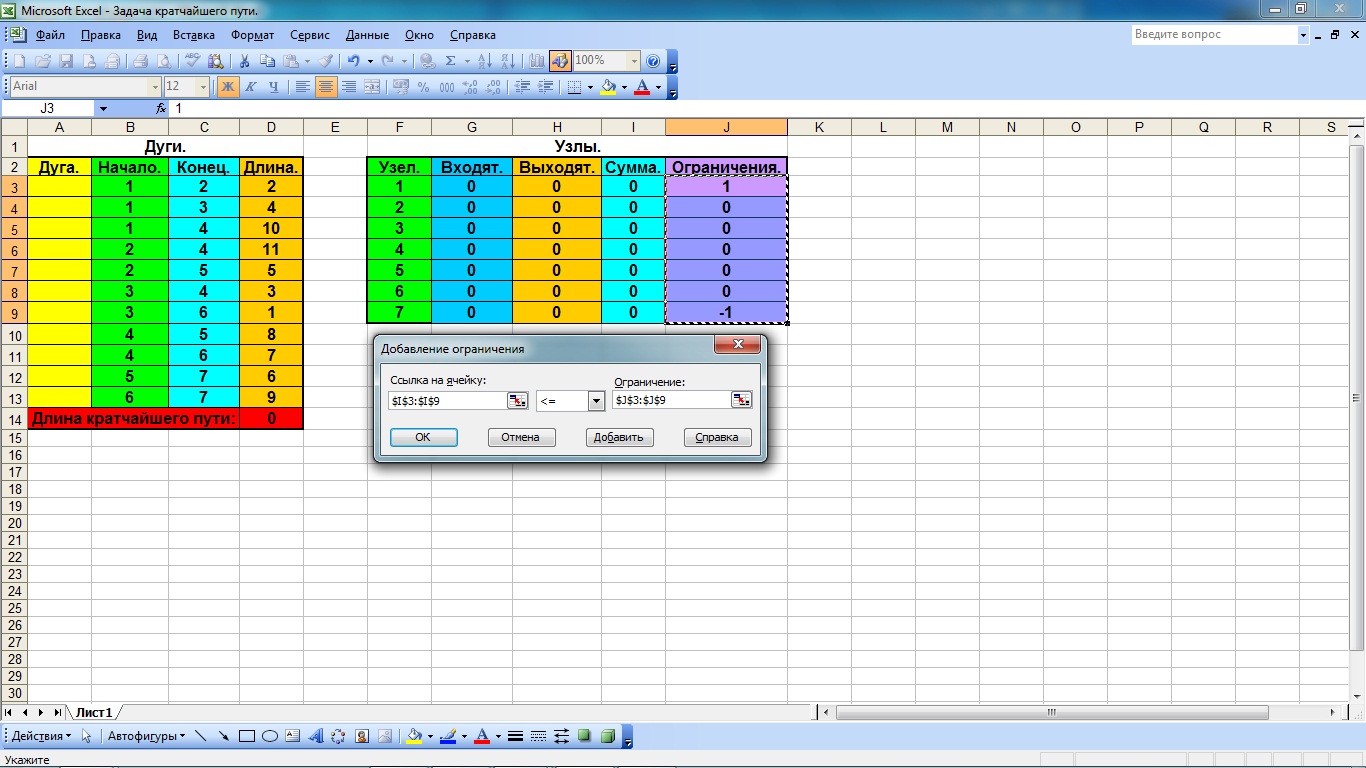
8) Вводим ограничения, выделив столбец «Ограничения» в таблице «Узлы».

9) Нажимаем кнопку ОК.

10). В окне «Поиск решения» нажимаем кнопку «Параметры», оставляем стандартные условия без изменения. Ставим галочку в чекбоксах «Линейная модель» и «Неотрицательные значения переменных». После чего нажимаем ОК (рис. 4.10).

11). Нажимаем кнопку «Выполнить» в окне «Поиск решения» и в появившемся окне результаты поиска решения нажимаем ОК (рис. 4.11).

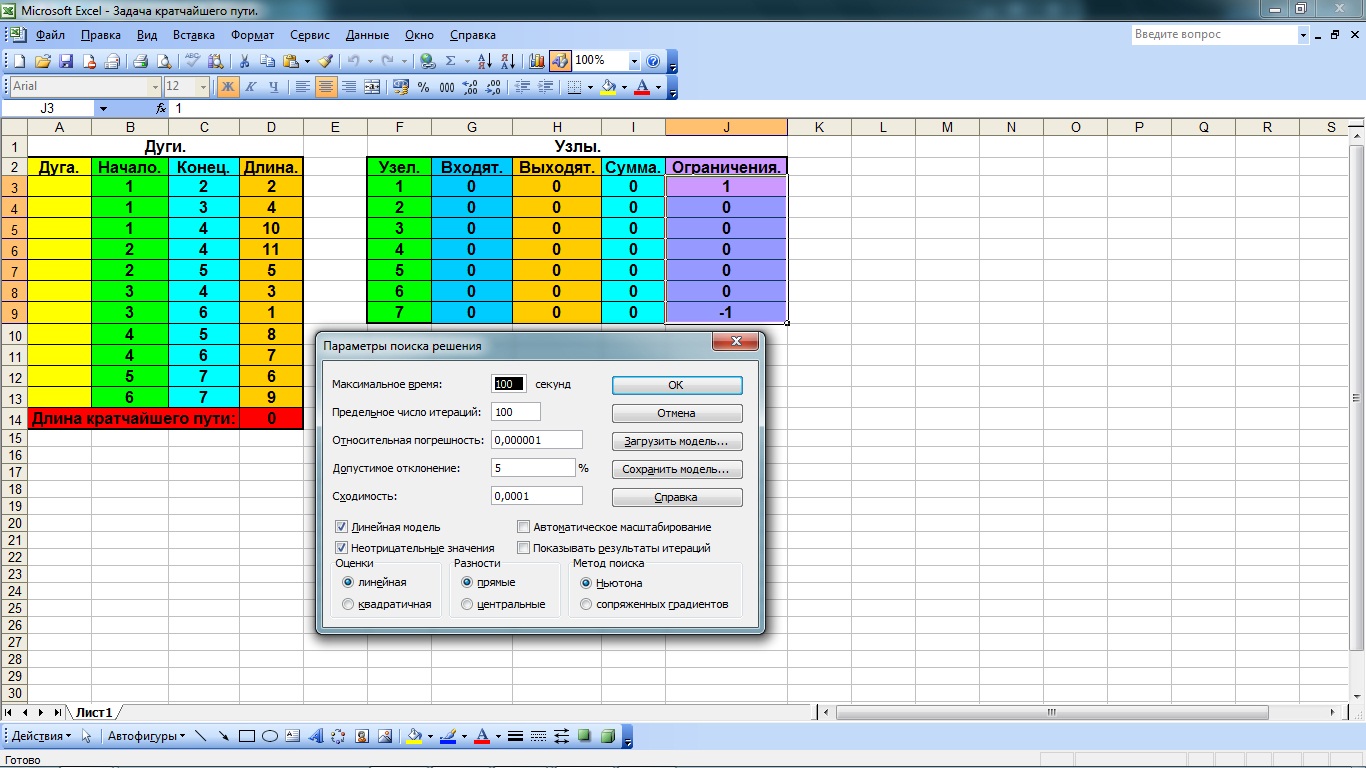
Рис. 4.10 Установка параметров поиска решения

Анализ результатов расчетов

Данные по решению задачи находятся в таблице «Дуги». Так в столбце «Дуга» размещены значения искомых переменных. Если они равны 0, то соответствующая дуга в строке таблицы не принадлежит кратчайшему пути. Если это значение равно 1 то дуга, соединяющая соответствующие узлы находится на критическом пути. В рассматриваемой задаче минимальное расстояние (стоимость, время) в 13 ед. обеспечивается при движении пот маршруту 1, 2, 5, 7.

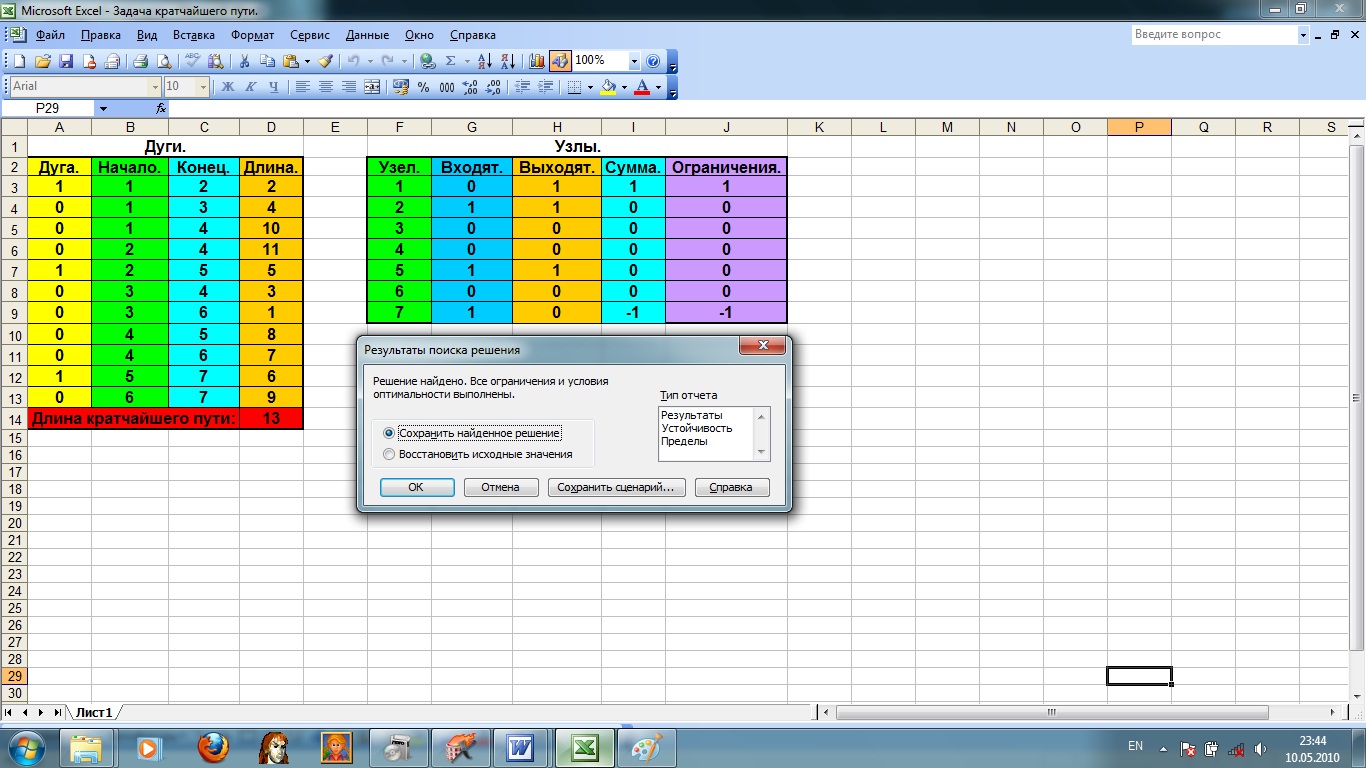
Рис. 4.11 Результаты поиска решения.