42. Построение нелинейных форм регрессионной зависимости.
Многие
экономические зависимости не являются
линейными, и поэтому их моделирование
линейными уравнениями регрессии не
может дать положительного результата.
Например, при анализе эластичности
спроса по цене применяется так называемая
логарифмическая модель, при анализе
издержек от объема выпуска – полиномиальная
(кубическая) модель. Достаточно широко
применяются и многие другие модели –
в частности, обратная и экспоненциальная
модели. Логарифмическая
модель Пусть
некоторая экономическая зависимость
моделируется формулой
,
где A, – параметры модели. Эта функция
может отражать зависимость спроса Y на
благо от его цены X
(в этом случае 0)
или от дохода X (0 – функция Энгеля).
Прологарифмировав обе части последнего
соотношения, получим
,
замена переменных вида
позволяет формально свести уравнение
к линейному виду:
.
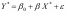По
МНК можно рассчитать значения параметров
аналогично случаю линейной модели (при
этом вместо наблюдений
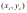рассматриваются наблюдения
).
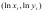Обратная
модель имеет вид
.
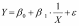Заменой
эта модель сводится к линейной. Модель
применяется, например, для характеристики
связи удельных расходов сырья, материалов,
топлива с объемом выпускаемой продукции.
Кроме этого, классическим примером
применения модели является кривая
Филлипса, характеризующая нелинейное
соотношение между нормой безработицы
x и процентом прироста заработной платы
y.
Степенная
функция вида
при m=3 (кубическая функция) в микроэкономике
моделирует зависимость общих издержек
от объема выпуска; квадратичная функция
(m=2) отражает зависимость между объемом
выпуска и средними или предельными
издержками (или между расходами на
рекламу и прибылью). Модель может быть
сведена к линейной модели множественной
регрессии с помощью замены
.
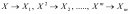Параметры модели ищут с помощью МНК.
Показательная
функция
может использоваться при анализе
изменения переменной Y с постоянным
темпом прироста во времени. Например,
производственная функция Кобба –
Дугласа с учетом научно – технического
прогресса:
.
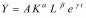Прологарифмировав, получаем соотношение:
,
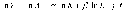которое сводится к линейному виду с помощью замен
.
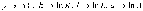44. Множественная линейная регрессия и корреляция.
На любой экономический показатель, чаще всего, оказывает влияние не один, а несколько факторов. Например, спрос на некое благо определяется не только ценой данного блага, но и ценами на замещающие и дополняющие блага, доходом потребителей и многими другими факторами. В этом случае рассматривается множественная регрессия:
.
Теоретическое линейное уравнение регрессии имеет вид:
,
или
для индивидуальных наблюдений
:
.
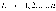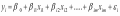Параметры
регрессии могут быть найдены в случае,
если
.
Самым распространенным методом оценки
параметров уравнения множественной
линейной регрессии также является
метод наименьших квадратов.