37. Критерии согласия Пирсона, Романовского, Колмогорова.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия, наиболее часто используемым является критерий согласия К. Пирсона («хи квадрат»). Ограничимся применением критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.

Пусть по выборке объема n получено эмпирическое распределение:

Варианты……………………

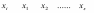
Эмпирические частоты…….

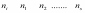
Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты 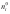. При уровне значимости требуется проверить нулевую гипотезу: генеральная совокупность распределена нормально.

В качестве критерия проверки нулевой гипотезы примем случайную величину:

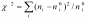(А)

Естественно, чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, и, следовательно, он характеризует близость эмпирического и теоретического распределений.

Доказано, что при n закон распределения случайной величины (А) стремится к закону распределения 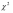с 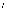степенями свободы независимо от того, какому закону распределения подчинена генеральная совокупность. Поэтому сам критерий называют критерием согласия .

Число степеней свободы определяется из равенства 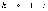, где s – число групп (частичных интервалов) выборки, r – число параметров предполагаемого распределения. В частности, если предполагаемое распределение – нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому число степеней свободы .

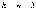Построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости :

.

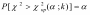Таким образом, правосторонняя критическая область определяется неравен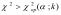ством , а область принятия нулевой гипотезы – соответственно неравенством 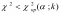. Обозначим значение критерия, вычисленного по данным наблюдений, через 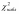и сформулируем правило проверки нулевой гипотезы:

Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу H₀: генеральная совокупность распределена нормально, необходимо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия 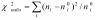и по таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы k=n–3 найти критическую точку 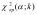. Если 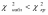– нет оснований отвергать нулевую гипотезу. В противном случае нулевую гипотезу отвергают, считая, что генеральная совокупность не распределена по нормальному закону.

Уравнения Колмогорова Пусть система имеет конечное число состояний и случайный процесс, протекающий в ней, характеризуется некоторыми вероятностями нахождения системы в каждом из состояний.

В случае марковской системы с непрерывным временем и конечным числом состояний их вероятности могут быть найдены с помощью решения системы дифференциальных уравнений Колмогорова:

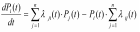, (2)

где .

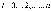Величина 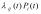называется потоком вероятности перехода из состояния 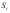в состояние .

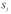Уравнения Колмогорова составляют по размеченному графу состояний системы, пользуясь следующим правилом: производная вероятности каждого состояния равна сумме всех потоков вероятности, идущих из других состояний в данное состояние, минус сумма всех потоков вероятности, идущих из данного состояния в другие.

Решение системы уравнений Колмогорова необходимо задать начальное распределение вероятносте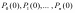й . Как правило, за исключением особенно простых систем, решение возможно получить лишь численными методами.