Полигон и гистограмма

Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

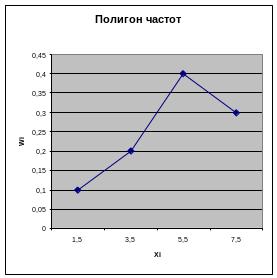
Полигоном частот называют ломаную линию, отрезки которой соединяют точки . Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты и соединяют точки отрезками прямых.

Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты .

В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала – сумму частот вариант, попавших в i–й интервал.

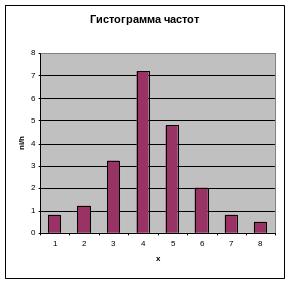
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению . Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте) . Площадь i–го прямоугольника равна – сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

В случае гистограммы относительных частот по оси ординат откладываются относительные частоты , на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте . Площадь i–го прямоугольника равна относительной частоте вариант , попавших в i–й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.

24. Статистический и вариационный ряд. Эмпирическая функция распределения и ее свойства. Вариационный ряд для дискретных и непрерывных случайных величин. Пусть из генеральной совокупности извлечена выборка, причем значение исследуемого параметра наблюдалось раз, - раз и т.д. При этом объем выборки. Наблюдаемые значения называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки - относительными частотами. Вариационный ряд можно представить таблицей вида:

X			..
n			.

Статистическим распределением выборки называют перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как:

X			…..
w			….

где относительные частоты .

Эмпирической функцией распределения называют функцию , определяющую для каждого значения x относительную частоту события X<x. Таким образом, по определению , где – число вариант, меньших x, n – объем выборки.

Свойства эмпирической функции распределения: 1) Значения эмпирической функции принадлежат отрезку [0,1]. 2) – неубывающая функция. 3) Если – наименьшая варианта, то =0 при , если – наибольшая варианта, то =1 при .

Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

25. Математическое ожидание, дисперсия, среднее квадратическое отклонение и моменты непрерывной случайной величины. Мода и медиана непрерывной случайной величины. Неравенство Коши-Буняковского.

Дисперсией непрерывной СВ наз-ся значение интеграла:

.

Среднее арифмитическое:

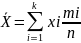
Мода ( ) непрерывной СВ – значение, кот соответствует максимальное знач ее плотности вероятности.

Медианой ( ) непрерывной СВ - значение, кот опр равенством:

.

Вариационный размах(или широта распр-ния): есть разность между наибольшим и наименьшим значениями выборочного расп-ния: R=xmax-xmin

Начальные и центральные моменты для непрерывных случайных величин находятся по формулам:

,

.

Асимметрией распределения случайной величины называется отношение центрального момента третьего порядка к кубу среднего квадратичного отклонения:

.

Эксцессом распределения случайной величины называют число, определяемое выражением:

.

Для нормального распределения 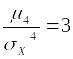, поэтому эксцесс равен нулю.

26. К точечной оценке предъявляется ряд требований. Она обязательно должна быть:

1. состоятельной (при увеличении объема выборки значение оценки должно стремиться (по вероятности) к истинному значению оцениваемого параметра );

2. несмещенной, т.е. чтобы ее математическое ожидание 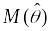было равно оцениваемому параметру ;

3. эффективной, т.е. иметь минимальную дисперсию.

За оценку вероятности события принимают его частость, за оценку математического ожидания – среднее значение полученных реализаций случайной величины .

Для построения интервальной оценки задаются малой вероятностью – уровнем значимости (или доверительной вероятностью ) и по полученной точечной оценке и объему выборки находят доверительный интервал.

28. Доверительным интервалом называется такой интервал значений оценки , который включает неизвестное истинное значение оцениваемого параметра с заданной вероятностью , называемой доверительной вероятностью:

– такая малая вероятность выхода истинного значения оцениваемого параметра за пределы интервала , которой можно пренебречь.

Доверительный интервал характеризует точность оценки параметра, а доверительная вероятность – ее надежность: чем больше доверительная вероятность, тем шире доверительный интервал при одном и том же объеме выборки, т.е. выигрывая в надежности оценки, проигрываем в ее точности и наоборот.

Для определения доверительного интервала необходимо знать закон распределения оценки .

29Доверительные интервалы для неизвестного математического ожидания и неизвестной дисперсии. Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение  этого распределения известно. Требуется оценить неизвестное математическое ожидание a по выборочному среднему . Найдем доверительные интервалы, покрывающие параметр a с надежностью .

Будем рассматривать выборочное среднее _, как случайную величину (т.к. меняется от выборки к выборке), и выборочные значения , как одинаково распределенные независимые случайные величины (эти числа также меняются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно a и среднее квадратическое отклонение – . Так как случайная величина X распределена нормально, то и выборочное среднее также распределено нормально. Параметры распределения равны:

.

Потребуем, чтобы выполнялось соотношение , где – заданная надежность.

Используем формулу .

Заменим X на и  на и получим:

,

где .

Выразив из последнего равенства , получим:

.

Так как вероятность P задана и равна , окончательно имеем:

.

Смысл полученного соотношения – с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр a, причем точность оценки равна .

Таким образом, задача решена. Число определяется из равенства ; по таблице функции Лапласа находят аргумент , которому соответствует значение функции Лапласа, равное .

Следует отметить два момента: 1) при возрастании объема выборки n число убывает и, следовательно, точность оценки увеличивается, 2) увеличение надежности оценки приводит к увеличению (так как функция Лапласа – возрастающая функция) и, следовательно, к возрастанию , то есть увеличение надежности оценки влечет за собой уменьшение ее точности.

Если требуется оценить математическое ожидание с наперед заданной точностью и надежностью , то минимальный объем выборки, который обеспечит эту точность, находят по формуле , следующей из равенства .