Основные теоретические положения

Если к зажимам электрической цепи (рис.1), состоящей из параллельно соединенных катушки индуктивности (с активным сопротивлением R_к и индуктивностью L) и конденсатором (емкостью С), приложено напряжение, меняющееся во времени по синусоидальному закону u (t) = U_m sin t , то токи в параллельных ветвях и неразветвленной части цепи также будут синусоидальными:

i_к (t) = sin (t - _к) = I_mк sin (t - _к) ;

i_с (t) = sin (t + _c) = I_mc sin (t + _c) ;

i (t) = i _к(t) + i _с(t) ,

где X_с = - сопротивление батареи конденсаторов;

X_к = L_к - индуктивное сопротивление катушки;

Z_к = - полное сопротивление катушки индуктивности;

; ;  = 2f ;

f – частота синусоидального тока.

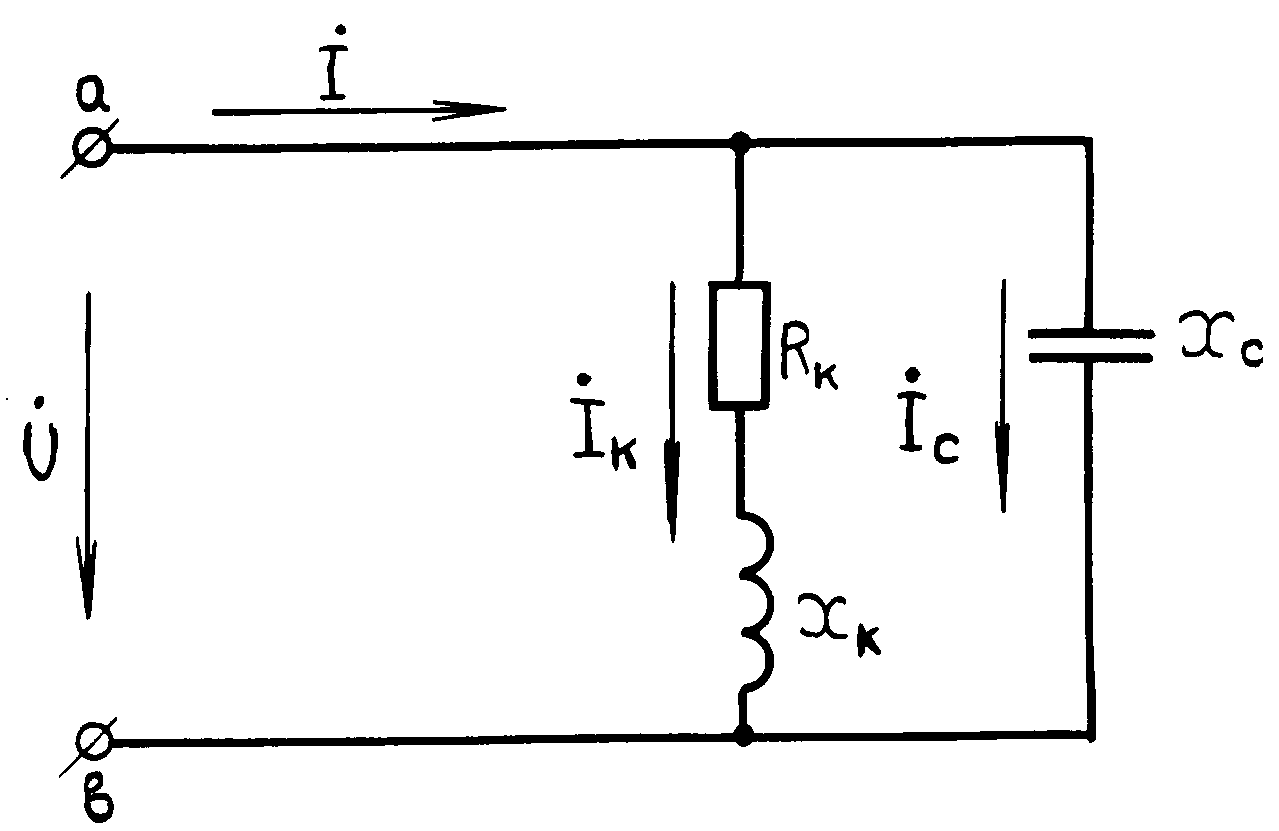
Рис. 1

По закону Ома в комплексной форме ток в катушке равен:

= = = =

= (g_к – j b_к) = Y_к = ,

где Y_к = g_к – j b_к - комплекс полной проводимости катушки;

- активная проводимость катушки;

- индуктивная проводимость катушки;

g_к - активная составляющая тока катушки, совпадающая по фазе с напряжением Ú;

– j b_к - реактивная составляющая тока катушки, отстающая по фазе от напряжения на  /2.

Ток в ветви с конденсатором равен: = = jС = jb_c .

Ток в неразветвленной части цепи определяется формулой

=

или = [g_к – j(b_к – b_c)] = Y ,

где Y = g_к – j (b_к – b_c) = ye^-j = y cos  + jy sin  - комплекс полной проводимости всей цепи (рис.1);  = arctg - угол между напряжением U, приложенным ко всей цепи, и током в неразветвленной части цепи I; y = - модуль полной проводимости цепи;

Векторная диаграмма токов (рис.2) строится на основании уравнения, составленного по первому закону Кирхгофа. Начальную фазу напряжения принимают равной нулю, то есть = U, вектор напряжения совмещается с осью +1 на комплексной плоскости.

На рис.2 приведена векторная диаграмма для случая, когда b_c  b_к (после резонанса) и напряжение отстает по фазе от тока на угол    /2. Ток в неразветвленной части цепи носит активно-емкостной характер ( I_c  I_кр).

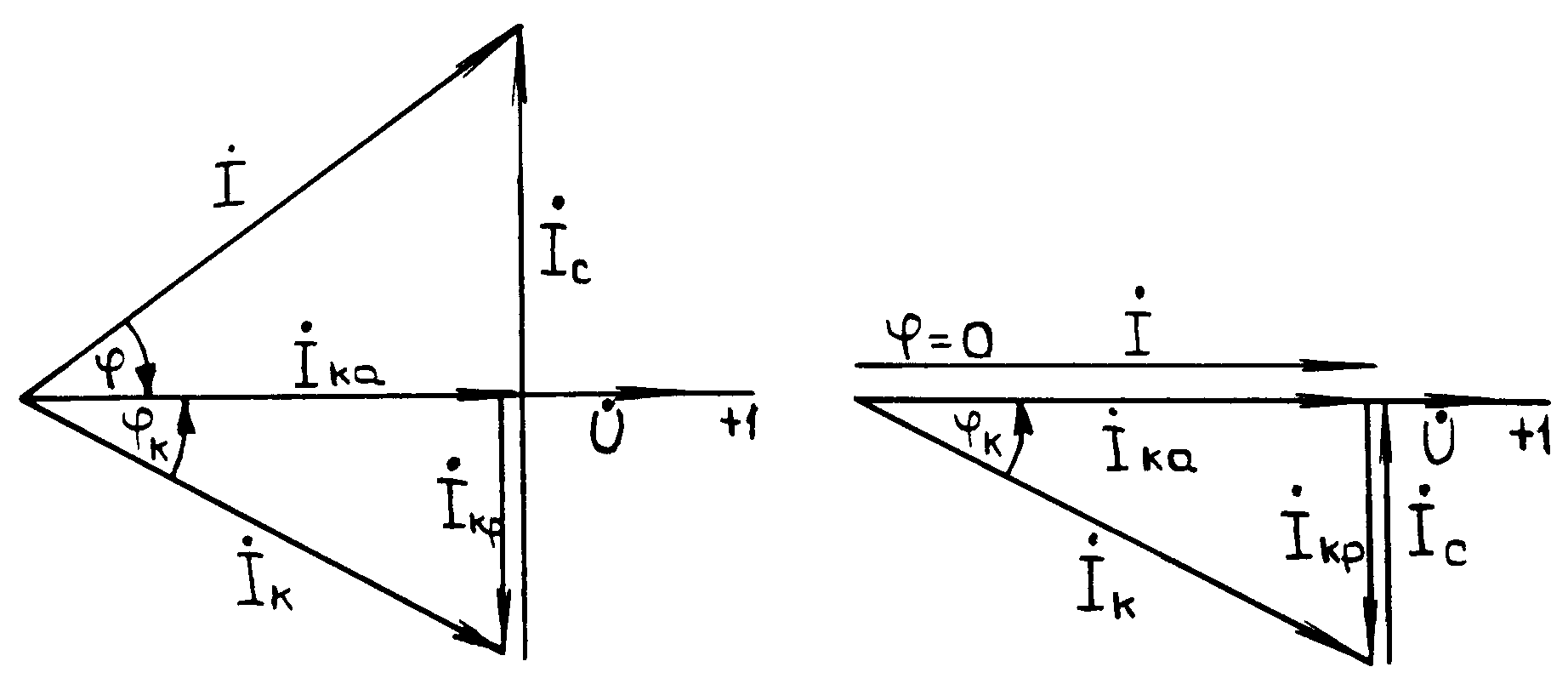
Рис.2 Рис.3

Резонансом тока называют явление в параллельной цепи с емкостными и индуктивными приемниками, когда общий ток в неразветвленной части цепи и напряжение на входе цепи совпадают по фазе. Резонанс токов характеризуется равенством реактивных токов в индуктивном и емкостном приемниках. Ток в неразветвленной части цепи минимальный, совпадает по фазе с напряжением и определяется активными составляющими токов емкостного и индуктивного приемников. Для цепи, представленной на рис.1, резонансное состояние характеризуется соотношениями:

, ,  = 0 .

Векторная диаграмма для резонансного режима представлена на рис.3.

Ток в неразветвленной части цепи определяется выражением

I = y U = U .

Поскольку при резонансе ток в неразветвленной части цепи чисто активный, то условием резонанса является равенство реактивных проводимостей приемников:

b_к = b_с или + ₀² L_к² = ₀C .

Это условие называется условием резонанса токов. Резонансное состояние можно получить, изменяя параметры цепи С, L_к , R_к или частоту напряжения сети .

Резонансная частота f₀ = ₀ / 2 определяется из условия резонанса

f₀ = .

Видно, что резонанс возможен лишь при условии R_к . При резонансе ток в цепи I минимален : I = gU.

Реактивные токи в приемниках могут оказаться больше активного тока в неразветвленной части цепи. Превышение реактивных токов приемников при резонансе по сравнению с активным током в неразветвленной части цепи характеризуют добротностью цепи q.

На рис. 3 показана векторная диаграмма токов для контура в режиме резонанса. В этом режиме входной ток достигает максимального значения и его амплитудное значение равно I_0m = U_1m/R. Если R является активным сопротивлением проводов катушки, то мощность

P = R учитывает активные потери мощности в ней. Потери мощности в конденсаторе для низких и средних частот составляют малую величину и в его схеме замещения не учитываются.

Амплитудные значения токов на реактивных элементах L и C в режиме резонанса могут значительно превышать входное напряжение

(4)

где  - характеристическое сопротивление последовательного колебательного конура

(5)

Отношение Q = /R - называется добротностью контура. Для контуров, применяемых в радиоэлектронике, величина Q достигает десятков и сотен единиц.

С целью оценки уровня искажения сигналов для колебательного контура используют понятие полосы пропускания (П). Полосой пропускания контура называют диапазон частот, в котором АЧХ уменьшается не более, чем в 2 раз по сравнению с ее значением при резонансной частоте, что соответствует на ЛАЧХ уменьшению характеристики на –3 дБ (рис. 5,а). Полоса пропускания контура П=ω_Г2 - ω_Г1 , где ω_Г1 и ω_Г2- граничные частоты полосы пропускания..

Мгновенная мощность в цепи есть произведение мгновенных значений тока и напряжения р(t) = u(t) i(t) .

Активная мощность – среднее за период значение мгновенной мощности, то есть активная мощность характеризует среднюю мощность преобразования энергии в цепи в другие виды энергии:

P = UI cos  .

При параллельном соединении

P = UI_a = U²g ,

где U и I – соответственно действующие значения напряжения и тока в цепи;

 - угол сдвига по фазе между током и напряжением в цепи, зависит от характера нагрузки; g - активная проводимость цепи.

Полная мощность цепи – мощность, подводимая к зажимам цепи и характеризующая амплитуду колебаний мощности в цепи. Определяют полную мощность произведением действующих значений тока и напряжения

S = UI .

Реактивная мощность цепи – мощность, периодически запасаемая в реактивных элементах и отдаваемая ими обратно генератору, равная:

Q = UI sin  .

Комплексная форма полной мощности

= Scos  + jS sin  = P + jQ

дает возможность построить векторную диаграмму мощностей – треугольник мощностей (рис.4). Из векторной диаграммы мощностей находим полную мощность: S =

При резонансе реактивная мощность цепи Q = 0. Реактивные мощности на участках цепи с L_к и C характеризуют взаимное преобразование энергии электрического и магнитного полей индуктивности и емкости. Активная мощность P = S.

Р езонанс токов используют в установках для повышения коэффициента мощности, подключая параллельно приемнику с сосредоточенными параметрами R, L конденсаторную батарею емкостью С:

C = I_c / 2fU = I_к sin _к / 2fU ,

которая обеспечивает полную компенсацию сдвига фаз между напряжением U и током I, при этом коэффициент мощности cos  = 1 и источник электрической энергии полностью разгружается от реактивного тока (S = P). Обычно коэффициент мощности установок доводят до 0,9…0,95. Еще большее повышение cos  требует больших затрат на установку батарей конденсаторов, которые экономически не оправдываются. В этом случае емкость батареи конденсаторов определяется формулой

C = (P / 2fU ²)(tg _н - tg ) ,

где P - активная мощность приемника; _н - угол сдвига по фазе приемника;  - требуемый угол сдвига по фазе.

Повышение коэффициента мощности установок снижает ток в линии электропередач, потери в линии P_л = I²R_л .

Порядок выполнения работы

Экспериментальное исследование линейной разветвленной электрической цепи синусоидального тока выполняют на установке, схема которой приведена на рис.5. Цепь состоит из параллельно соединенных индуктивной катушки L и конденсатора С.

Для измерения комплекса амплитудного значения тока Im и комплексного входного сопротивления -

необходимо воспользоваться комбинированным прибором измерителя мощности и фазы (ИМФ1). Он позволяет проводить измерения амплитудных значений синусоидального тока и падения напряжения на участке исследуемой цепи, а также разности фаз между током и напряжением. Измерительная схема представлена на рис. 5.

Для определения комплекса амплитудного значения напряжения на элементе Z2 ( U _Rm , U _Lm и U_Cm ), комплексной передаточной функции по напряжению использовать комбинированный прибор измерения мощности и фазы (ИМФ1). Он позволяет проводить измерения амплитудных значений падений напряжения на участках исследуемой цепи, а также разности фаз между ними. Измерительная схема представлена на рис. 5.

Рис.5