5.Построение графиков функций средствами дифференциального исчисления.

При исследовании функции и построении ее графика полезно воспользоваться следующей схемой.

1. Найти область определения функции.

2. Определить четность или нечетность функции.

3. Найти точки пересечения графика с осями координат, если это возможно.

4. Исследовать функцию на непрерывность. Найти асимптоты графика функции.

5. Найти интервалы монотонности и точки экстремума функции.

6. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.

7. Найти значение функции в нескольких дополнительных точках.

На основании проведенного исследования можно построить график.

Пример 1. Исследуйте функцию с помощью производной и постройте ее график.

Решение.

1. Найдем область определения функции. Это будет вся числовая ось, кроме точек, в которых знаменатель обращается в 0.

. .

2. Функция является нечетной, т.к. , ее график симметричен относительно начала координат (значит, график можно построить только при х≥0, а затем в силу нечетности функции отобразить его симметрично относительно начала координат).

3. Точка пересечения с осями координат: - начало координат.

4. Асимптоты графика:

а) вертикальные

б) наклонные , где

.

-горизонтальная асимптота - ось - при .

5. Проведем полное исследование по первой производной.

Н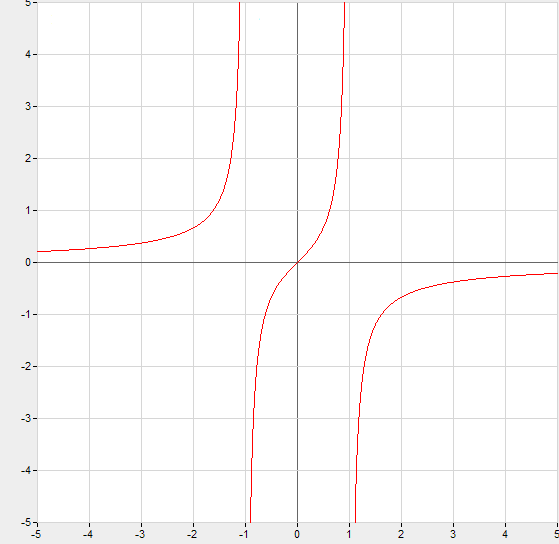 етрудно заметить, что при любом значении области определения функции, производная , т.е. функция является всюду возрастающей. Точек экстремума нет.

8. Проведем полное исследование по второй производной.

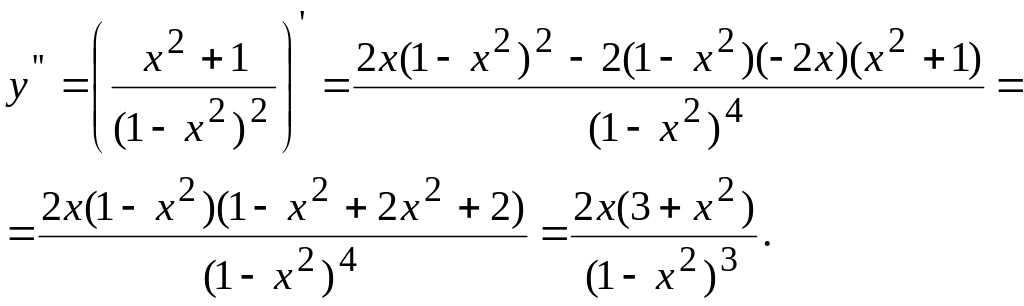
при .

Точка является точкой перегиба графика функции . Нанесем на чертеж все полученные точки и линии.

Пример 2. Исследуйте функцию с помощью производной и постройте ее график.

Решение

1. Область определения:

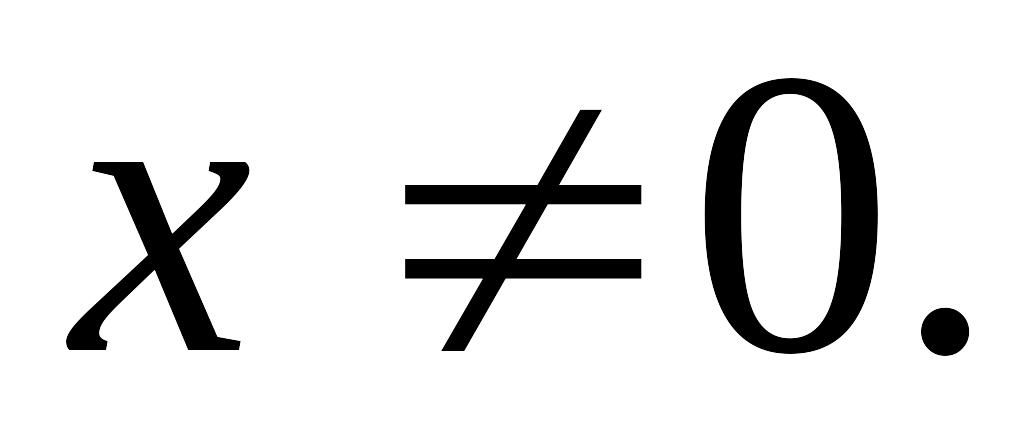
2. Данная функция нечетная, так как 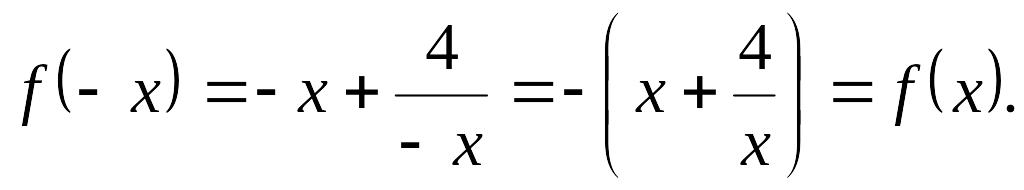Следовательно, график этой функции симметричен относительно начала координат. Поэтому сначала исследуем эту функцию и построим ее график при .

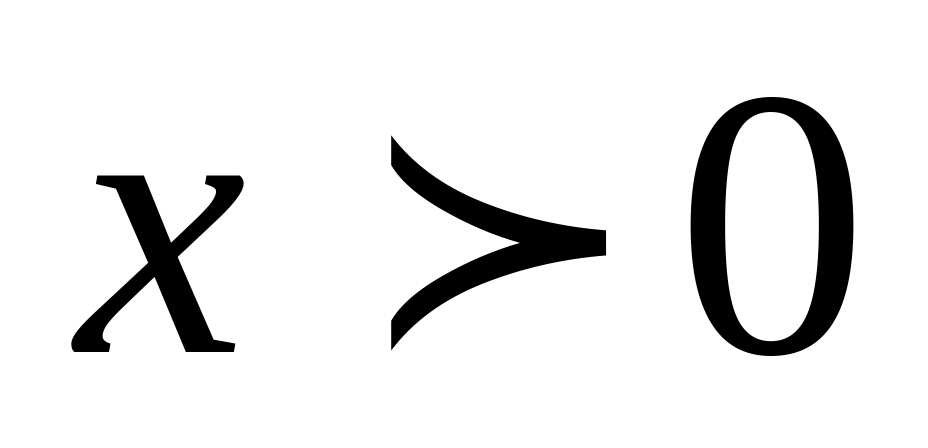3. Точки пересечения с осью Ох: у=0, 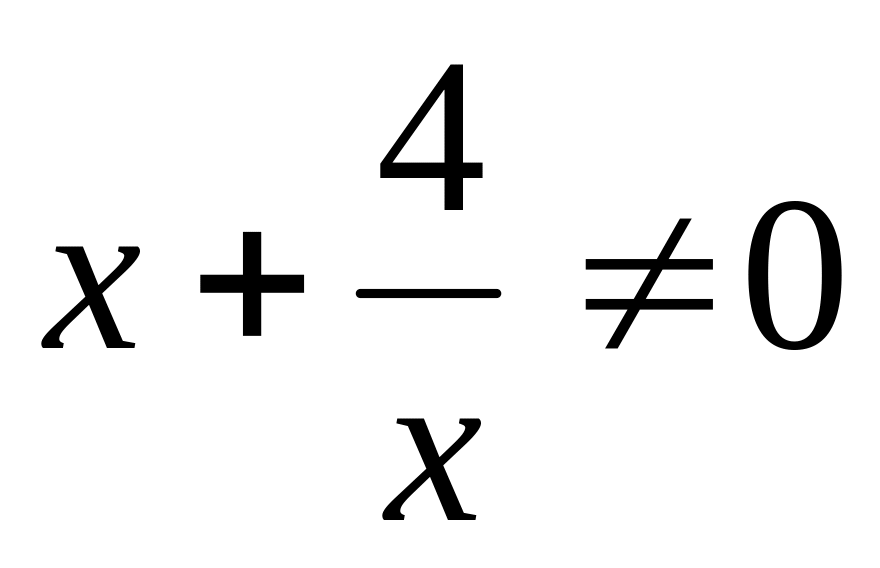, таких точек нет.

Точек пересечения с Оу тоже нет, так как х=0 не входит в область определения.

4. Найдем асимптоты функции.

Прямая х=0 является вертикальной асимптотой.

Наклонные асимптоты , где

.

-наклонная асимптота при .

5. Найдем точки экстремума функции

На промежутке x>0 функция имеет одну стационарную точку x=2.

Производная положительна на промежутке x>2, следовательно, на этом промежутке функция возрастает. На интервале 0<x<2 производная отрицательна, следовательно, на этом интервале функция убывает.

Точка x=2 является точкой минимума, так как при переходе через эту точку производная меняет знак с «-» на «+»;

Составим таблицу:

x	(0;2)	2	(2;+ )
F(x)		0	+
F (x)		4

6) Найдем интервалы выпуклости функции и точки перегиба

Так как ни при каких х вторая производная не равна 0, то точек перегиба нет.

7) Найдем значения функции еще в двух точках:

Используя результаты исследования, стоим график функции при x>0. График этой функции при x<0 строим с помощью симметрии относительно начала координат.