Сравнение методов расчета оптимальной цены
p0 |
|
|
5 |
52,53 |
60 |
20 |
60,03 |
60 |
30 |
65,03 |
60 |
40 |
70,03 |
80 |
60 |
80,03 |
90 |
Проанализируем результаты, представленные в табл. 2 и 3.
Функция спроса убывает, коэффициент a* отрицателен, поэтому рано или поздно прямая уйдет в отрицательную область. Это значит, что приближение функции спроса линейной зависимостью может быть корректно лишь на некотором отрезке, а не на всей прямой. Выясним, при какой цене спрос достигает 0:
D*(p) = (-0,4621)p +46,24062= 0,
p
=
=
100,066 руб.
Т.е. корректное приближение функции спроса линейной зависимостью может быть при цене p меньшей, чем 100,1 рубль.
Общепринятых простых методов, позволяющих избежать отрицательных оценок функции спроса, нет. Если получаем отрицательные величины, то должны указать область, в которой линейная зависимость дает корректную оценку.
Рассмотрим теперь табл.3. Здесь видим разницу между расчетной оптимальной ценой pопт.2, полученной с помощью метода наименьших квадратов, и расчетной ценой pопт.1, найденной исходя только из данных опроса. Это связано с тем, что потребитель всегда склонен к круглым числам. Мы же при применении метода наименьших квадратов ищем максимум не только среди названных опрошенными значений, а по более обширному множеству.
3 Степенная аппроксимация
Предположим, что функция спроса принадлежит к степенному семейству.
D(p) = cpa.
Чтобы привести функцию к линейному виду , нужно выполнить преобразование переменных. Прологарифмируем обе части равенства:
ln D(p)= ln C+ α ln p
Чтобы привести задачу к ранее рассмотренной задаче оценивания параметров линейной функции, введем обозначения:
t= ln p, x(t)= ln D(p), b= ln C
Получаем линейное уравнение:
x(t)= αt+b
Задача оценивания параметров степенной зависимости сведена к ранее рассмотренной задаче оценивания параметров линейной функции.
α*
=
b*
=
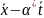
Запишем восстановленную зависимость:
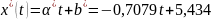
Вернемся к степенной функции:
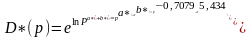
Таким образом, восстановленная функция спроса имеет вид:
Таблица 4
Оценивание функции спроса методом наименьших квадратов
№ (i) |
Цена (pi), руб. |
ti |
Ni |
D(pi) |
x(ti) |
x(ti)*Ni |
ti*Ni |
ti2*Ni |
|
x*(ti) |
x(ti)-x*(ti)
|
D*(pi) |
Ni∙[D(pi)-D*(pi)] |
Ni∙[D(pi)-D*(pi)]2 |
|||
1 |
5 |
1,609438 |
6 |
50 |
3,912023 |
23,47214 |
9,656627 |
15,54174 |
37,77694884 |
4,294679 |
-0,382655896 |
73,3087 |
-139,8521 |
19558,6059 |
|||
2 |
10 |
2,302585 |
5 |
44 |
3,78419 |
18,92095 |
11,51293 |
26,50949 |
43,5670932 |
3,804 |
-0,019810379 |
44,8804 |
-4,4018 |
19,3756 |
|||
3 |
15 |
2,70805 |
5 |
39 |
3,663562 |
18,31781 |
13,54025 |
36,66768 |
49,60554426 |
3,516971 |
0,146590383 |
33,6823 |
26,5887 |
706,9580 |
|||
4 |
20 |
2,995732 |
4 |
34 |
3,526361 |
14,10544 |
11,98293 |
35,89765 |
42,25612813 |
3,313321 |
0,213039401 |
27,4762 |
26,0951 |
680,9533 |
|||
5 |
25 |
|
3 |
30 |
3,401197 |
10,20359 |
9,656627 |
31,08348 |
32,84409608 |
3,155358 |
0,245839578 |
23,4614 |
19,6157 |
384,7757 |
|||
6 |
30 |
3,401197 |
2 |
27 |
3,295837 |
6,591674 |
6,802395 |
23,13629 |
22,41958344 |
3,026292 |
0,269544492 |
20,6206 |
12,7587 |
162,7849 |
|||
7 |
35 |
3,555348 |
1 |
25 |
3,218876 |
3,218876 |
3,555348 |
12,6405 |
11,44422392 |
2,917169 |
0,301706718 |
18,4889 |
6,5111 |
42,3947 |
|||
8 |
40 |
3,688879 |
3 |
24 |
3,178054 |
9,534161 |
11,06664 |
40,82349 |
35,17037244 |
2,822642 |
0,355411596 |
16,8212 |
21,5363 |
463,8114 |
|||
9 |
45 |
|
1 |
21 |
3,044522 |
3,044522 |
3,806662 |
14,49068 |
11,58946936 |
2,739264 |
0,305258814 |
15,4756 |
5,5244 |
30,5191 |
|||
10 |
50 |
3,912023 |
1 |
20 |
2,995732 |
2,995732 |
3,912023 |
15,30392 |
11,71937357 |
2,664679 |
0,331053359 |
14,3633 |
5,6367 |
31,7719 |
|||
11 |
55 |
4,007333 |
1 |
19 |
2,944439 |
2,944439 |
4,007333 |
16,05872 |
11,79934803 |
2,597209 |
0,347230141 |
13,4262 |
5,5738 |
31,0671 |
|||
12 |
60 |
4,094345 |
3 |
18 |
2,890372 |
8,671115 |
12,28303 |
50,29097 |
35,50253367 |
2,535613 |
0,354758273 |
12,6242 |
16,1275 |
260,0955 |
|||
13 |
65 |
4,174387 |
2 |
15 |
2,70805 |
5,4161 |
8,348775 |
34,85102 |
22,60890057 |
2,478951 |
0,229098949 |
11,9287 |
6,1425 |
37,7303 |
|||
14 |
70 |
4,248495 |
2 |
13 |
2,564949 |
5,129899 |
8,49699 |
36,09942 |
21,79435028 |
2,42649 |
0,138459139 |
11,3191 |
3,3618 |
11,3019 |
|||
15 |
75 |
4,317488 |
1 |
11 |
2,397895 |
2,397895 |
4,317488 |
18,6407 |
10,35288434 |
2,37765 |
0,020245108 |
10,7795 |
0,2205 |
0,0486 |
|||
16 |
80 |
4,382027 |
3 |
10 |
2,302585 |
6,907755 |
13,14608 |
57,60647 |
30,26996762 |
2,331963 |
-0,029378252 |
10,2981 |
-0,8944 |
0,8000 |
|||
17 |
85 |
4,442651 |
1 |
7 |
1,94591 |
1,94591 |
4,442651 |
19,73715 |
8,645000169 |
2,289047 |
-0,343137026 |
9,8655 |
-2,8655 |
8,2113 |
|||
18 |
90 |
4,49981 |
1 |
6 |
1,791759 |
1,791759 |
4,49981 |
20,24829 |
8,062576587 |
2,248585 |
-0,456825265 |
9,4743 |
-3,4743 |
12,0709 |
|||
19 |
95 |
4,553877 |
1 |
5 |
1,609438 |
1,609438 |
4,553877 |
20,73779 |
7,329182118 |
2,210311 |
-0,600872636 |
9,1185 |
-4,1185 |
16,9624 |
|||
20 |
100 |
4,60517 |
4 |
4 |
1,386294 |
5,545177 |
18,42068 |
84,83037 |
25,53648584 |
2,174 |
-0,787705664 |
8,7934 |
-19,1736 |
367,6252 |
|||
sum |
|
|
50 |
422 |
|
152,7644 |
168,0099 |
611,1958 |
480,2940625 |
|
0,333 |
396,2 |
-19,0875 |
22827,8638 |
|||
sum/n |
|
|
|
|
3,055288 |
3,360198 |
12,22392 |
9,605881249 |
|
|
|
|
SS |
||||
Критерий
правильности расчета для степенной
модели: ∑(x(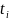
)-
x*(
))
= 0,а
также чередование знаков в этом столбце.
Сумма по этому столбцу дает 0,33, а не 0. Незначительное отличие от 0 связано с тем, что появляется ошибка округления при вычислении.
Рисунок 3 Функции спроса
Из табл.4 видно, что остаточная сумма квадратов SS = 22827,86 Исходя из этого, найдем оценку среднего квадратического отклонения:
Затем найдем доверительные границы для функции спроса:
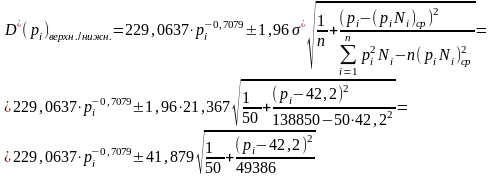
Например, при p = 40 руб.
D*(40) верхн. = 16,821 + 5,937 = 22,758,
D*(40)нижн. = 16,821 – 5,937 = 10,884.
Таким образом, при цене 40 руб. товар купят 11-23 человек
Теперь перейдем к расчету оптимальной цены при различных значениях оптовой цены (издержек) p0. Для этого мы должны максимизировать прибыль:
Продифференцируем это выражение по p и приравняем к нулю производную:
,
,
.
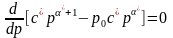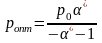Поскольку α*=-0,7079, то
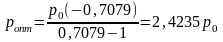
Сравним оптимальные розничные цены, найденные с помощью метода наименьших квадратов (pопт.3) и рассчитанные ранее с помощью первого метода (pопт.1).
Сравнение методов расчета оптимальной цены Таблица 5
p0, руб. |
pопт.1, руб. |
pопт.3, руб. |
5 |
60 |
12,1175 |
20 |
60 |
48,47 |
30 |
60 |
72,705 |
40 |
80 |
96,94 |
60 |
90 |
145,41 |