3. Циклограмма работы кулачкового механизма

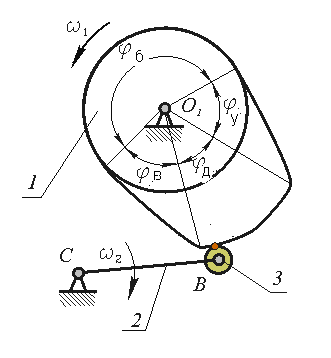
Рис. 2

Большинство кулачковых механизмов относится к цикловым механизмам с периодом цикла равным 2. В цикле движения толкателя в общем случае можно выделить четыре фазы (рис. 2): удаления из самого близкого (по отношению к центру вращения кулачка) в самое дальнее положение, дальнего стояния (или выстоя в самом дальнем положении), возвращения из самого дальнего положения в самое близкое и ближнего стояния (выстоя в самом ближнем положении). В соответствии с этим, углы поворота кулачка или фазовые углы делятся на:

• угол удаления _y

• угол дальнего стояния _д

• угол возвращения _в

• угол ближнего стояния _б.

Сумму φ_у + φ_д + φ_в называют рабочим углом и обозначают φ_р. Сле­довательно,

φ_у + φ_д + φ_в = φ_р.

4. Угол давления и угол передачи движения

Угол давления ϑ определяет положение нормали п-п в высшей КП относительно вектора скорости и контактной точки ведомого звена (рис. 3, а, б). Его величина определяется размерами механизма, передаточной функцией и перемещения толкателя S_.

Угол передачи движения γ - угол между векторами υ₂ и υ_отн абсолютной и относительной (по отношению к кулачку) скоростей той точки толкателя, которая находится в точке контакта А (рис. 3, а, б):

.

Если пренебречь силой трения между кулачком и толкателем, то силой, приводящей в движение толкатель (движущей силой), является давление Q кулач­ка, приложенное к толкателю в точке А и направленное по общей нор­мали п-п к профилям кулачка и толкателя. Разложим силу Q на взаимно перпендикулярные составляющие Q₁ и Q₂, из которых первая направ­лена по направлению скорости υ₂. Сила Q₁ перемещает толкатель, преодолевая при этом все полезные (связанные с выполнением технологических задач) и вредные (силы тре­ния) сопротивления, приложенные к толкателю. Сила Q₂ увеличива­ет силы трения в кинематической паре, образованной толкателем и стойкой.

Очевидно, что с уменьшением угла γ сила Q₁ уменьшается, а сила Q₂ увеличивается. При некотором значении угла γ может оказаться, что сила Q₁ не сможет преодолеть все сопротивле­ния, приложенные к толкателю, и механизм не будет работать. Такое явление называют заклиниванием механизма, а угол γ, при котором оно имеет место, называют углом заклинивания γ_закл .

При проектировании кулачкового механизма задают допускаемое значение угла давления ϑ_доп , обеспечивающее выполнения условия γ ≥ γ _min > γ _закл , т. е. текущий угол γ ни в одном положении ку­лачкового механизма не должен быть меньше минимального угла передачи γ _min и значительно превосходить угол заклинивания γ_закл .

Для кулачковых механизмов с поступательно движущимся толкателем рекомендуется γ _min = 60° (рис. 3, а) и γ_min = 45° - механизмов с вращающимся толкателем (рис. 3, б).

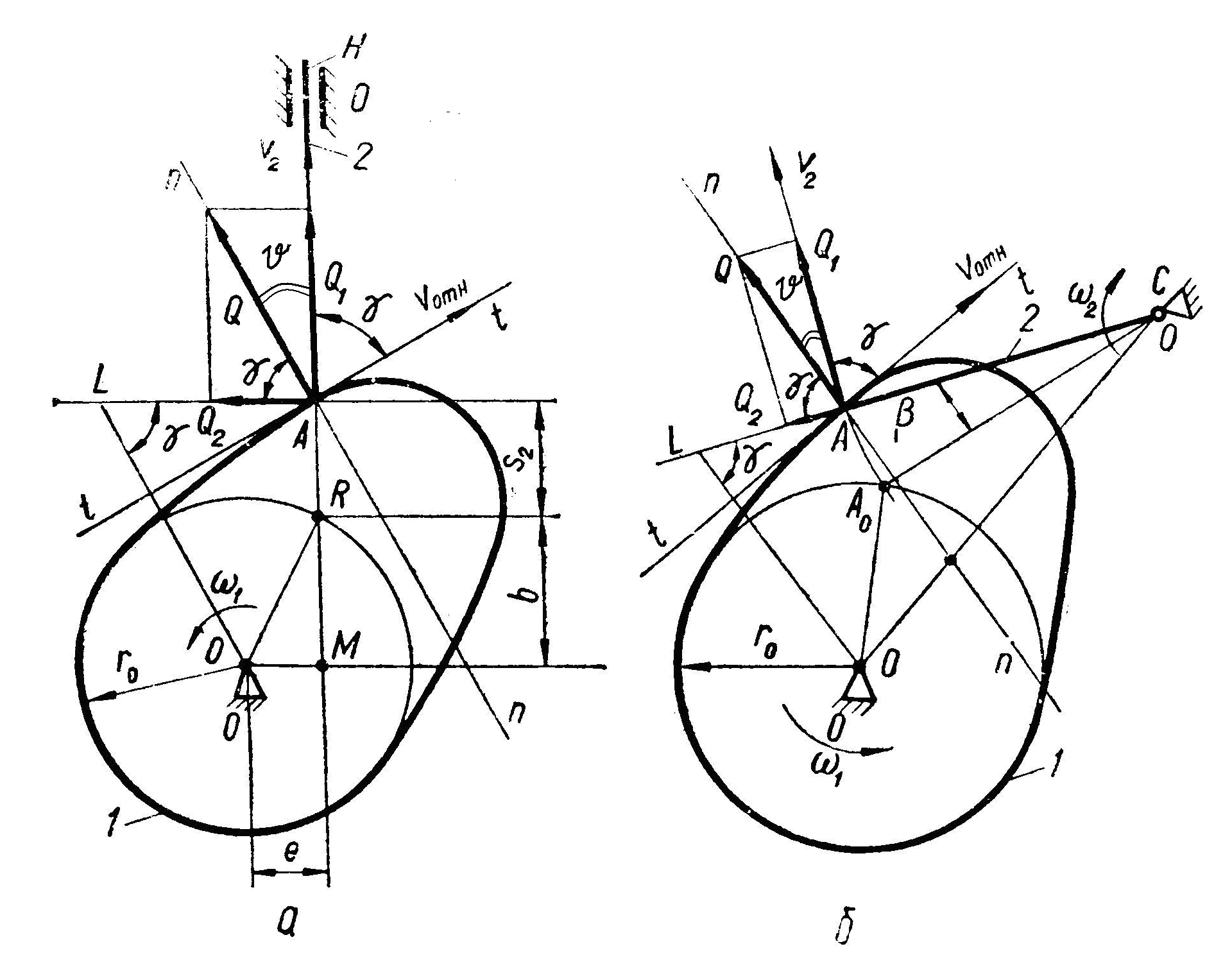
Рис. 3