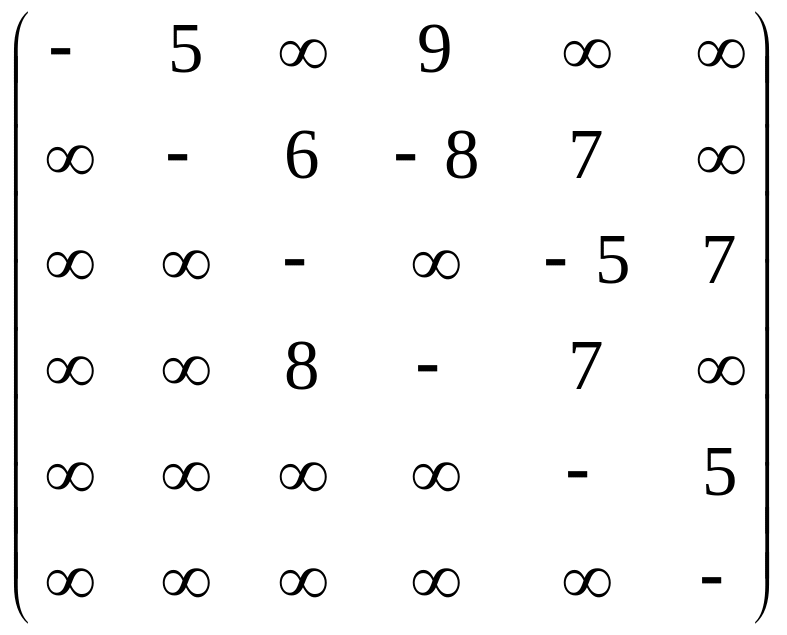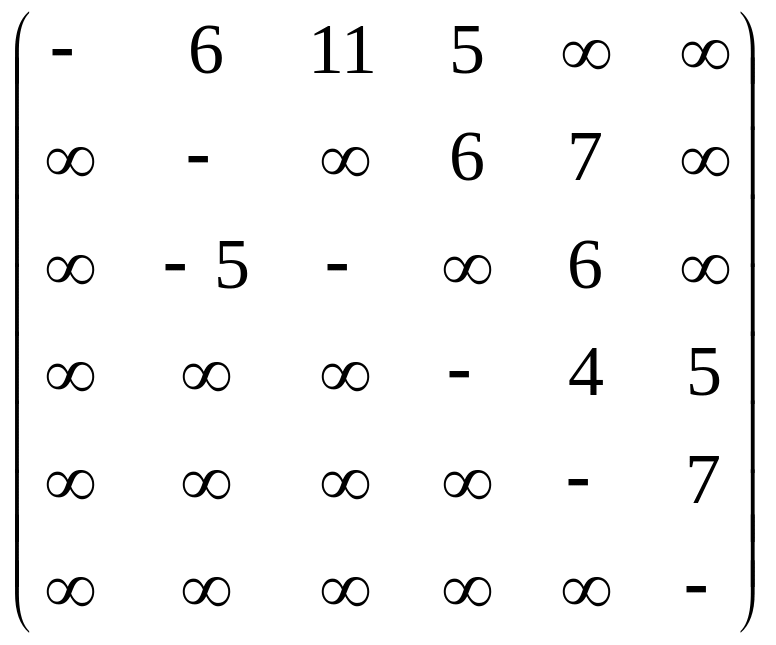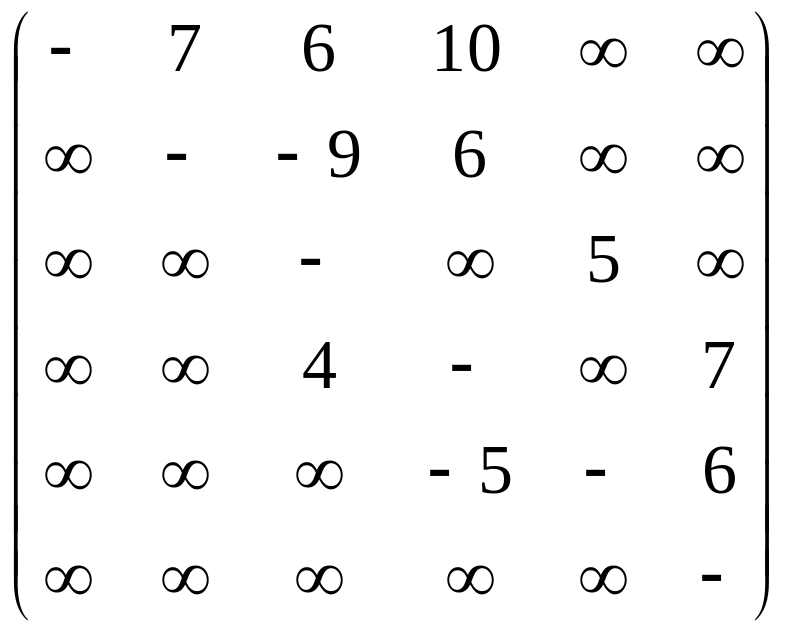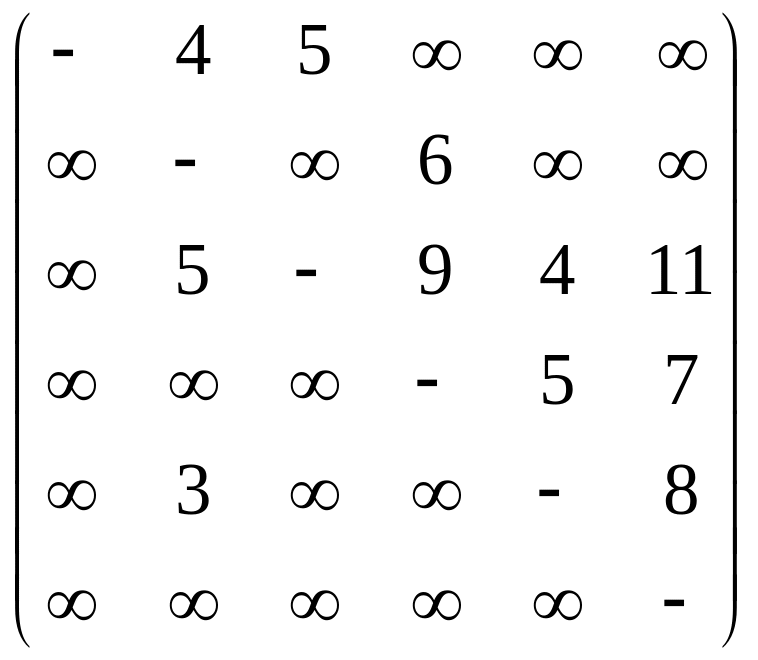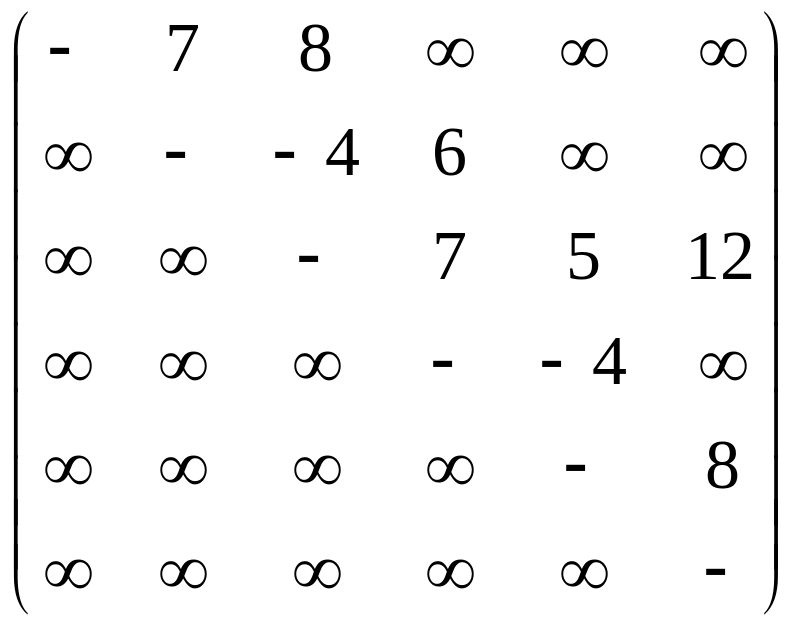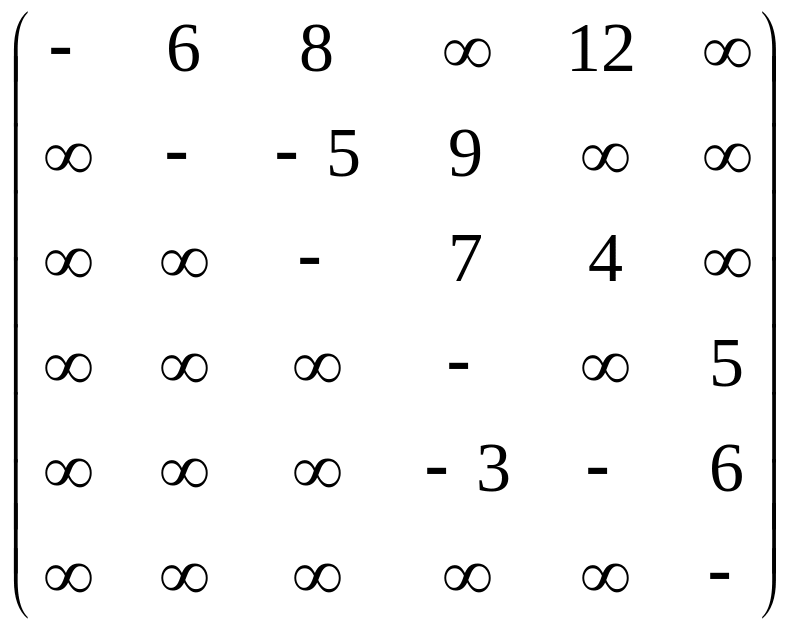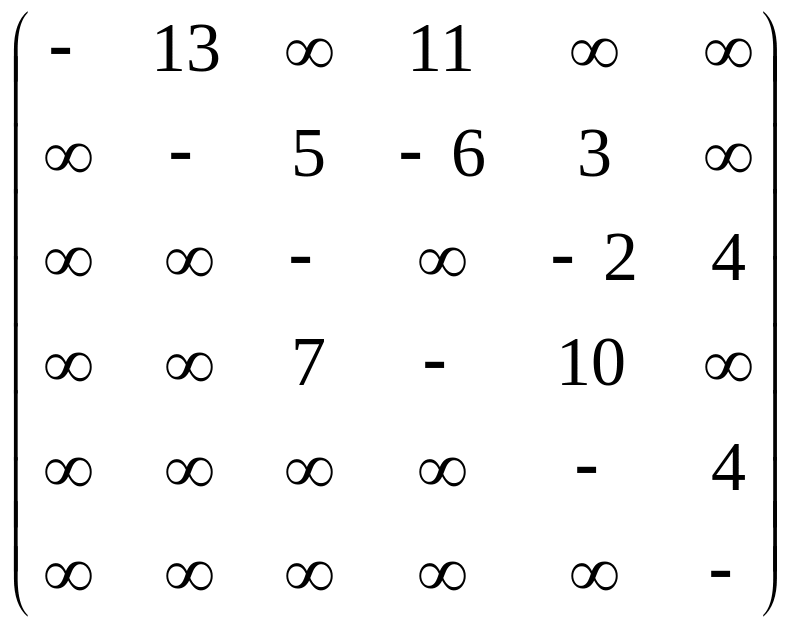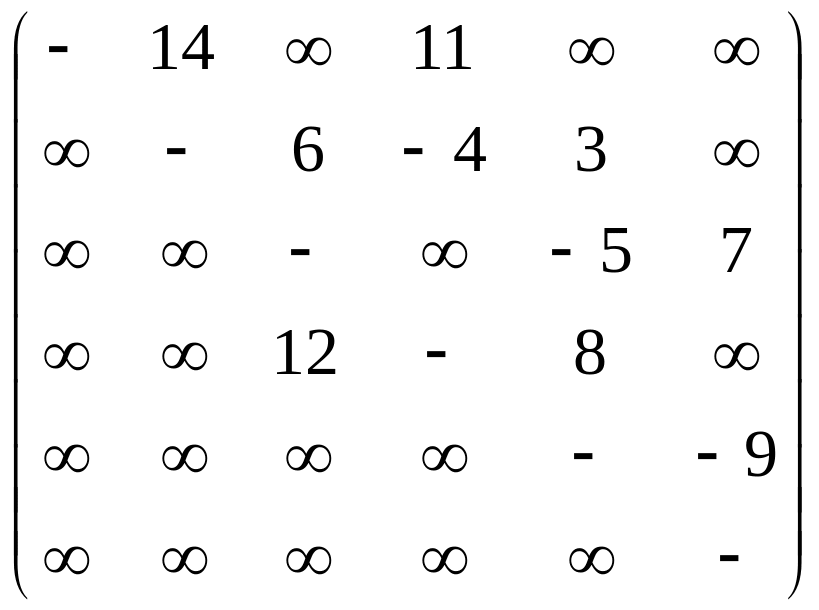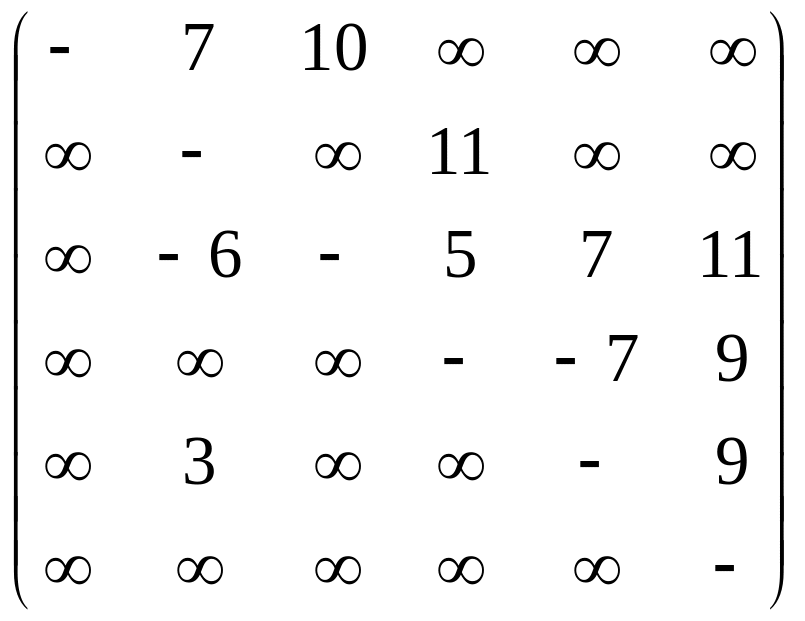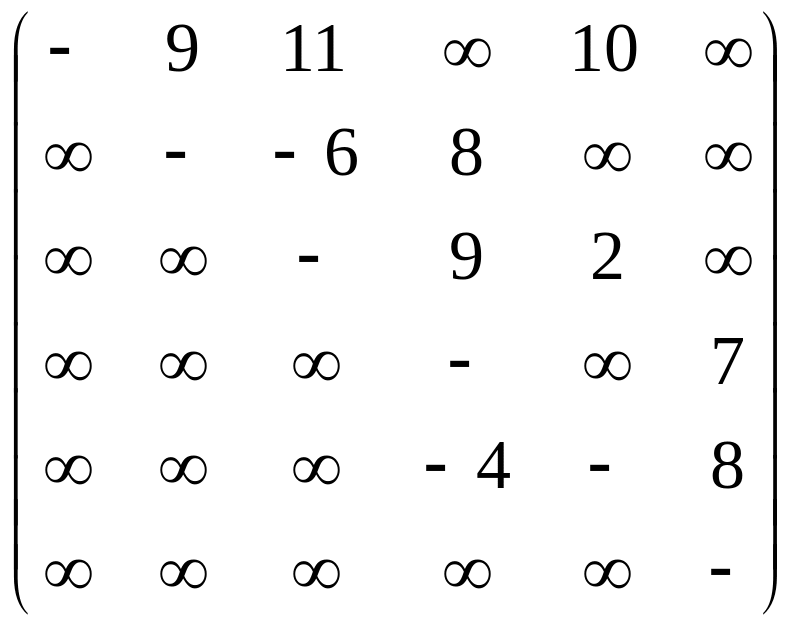Пример плана программы, реализующей алгоритм Беллмана-Форда для системы matlab.

Предположим, что имеется ориентированная сеть, имеющая шесть узлов, и множество дуг имеют веса произвольного знака. Пусть сеть задана с помощью матрицы смежности . Необходимо найти кратчайший путь от узла до узла . Приведем один из возможных вариантов плана программы для реализации алгоритма Беллмана-Форда.

Этап 1:

1. Задать матрицу W;

2. Задать вектор меток: d=[0 inf inf inf inf inf];

3. Задать вспомогательную переменную: a=0;

4. Для всех i=0:5 выполнить

Для всех j=1:6 выполнить

Для всех k=1:6 выполнить

Проверить W(j,k)~=inf? Если верно, заменить метку:

d(k)=min(d(k),d(j)+W(j,k));

5. Для всех j=1:6 выполнить

Для всех k=1:6 выполнить

Проверить W(j,k)~=inf? Если верно:

Проверить d(k)>d(j)+W(j,k)? Если верно, выполнить:

a=1;

6. Проверить а==1? Если верно:

Вывести на экран сообщение о невозможности решения задачи;

Иначе

Длины кратчайших путей до узлов сети найдены: M=d

Перейти к этапу 2.

Этап 2:

11. Задать начальное состояние для вектора пути: Way=6;

12. Найти узел 6: u=6;

13. Проверить условие: u~=1? Если верно, то выполнить

    1. Найти множество узлов, предшествующих u: P=W(:,u);

    2. Для всех i=1:6 выполнить

Проверить P(i)~=inf? Если верно, выполнить:

Проверить d(u)=d(i)+P(i)? Если верно, выполнить

u=i;

3. Выполнить: Way=[u,Way];

1. Кратчайший путь найден; он проходит через узлы с номерами: Way

Расчетно-графическая работа № 1

Построение кратчайших и максимальных путей

В ориентированной сети

Задание:

Изобразить в виде рисунков ориентированные сети , , заданные весовыми матрицами и . Построить для сети кратчайший путь от узла до с помощью алгоритма Дейкстры и максимальный путь. Построить для сети кратчайший путь от узла до с помощью алгоритма Беллмана-Форда.

Таблица 1. Варианты заданий

Номер варианта
1
2
3
4
5
6
7
8
9.
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30