Попередній аналіз і згладжування часових рядів економічних показників

Попередній аналіз тимчасових рядів економічних показників полягає в основному у виявленні і усуненні аномальних значень рівнів ряду, а також у визначенні наявності тренду в початковому часовому ряду.

Під аномальним рівнем розуміють окреме значення рівня часового ряду, яке не відповідає потенційним можливостям досліджуваної економічної системи і яке, залишаючись в якості рівня ряду, істотно впливає на значення основних характеристик часового ряду, у тому числі на відповідну трендову модель. Причинами аномальних спостережень можуть бути помилки технічного порядку, або помилки першого роду: помилки при агрегації і дезагрегуванні показників, при передачі інформації і ін. технічні причини. Помилки першого роду підлягають виявленню і усуненню. Крім того, аномальні рівні в тимчасових рядах можуть виникати через вплив чинників, що мають об’єктивний характер, але що проявляються епізодично, дуже рідко – помилки другого роду; вони усуненню не підлягають.

Для виявлення аномальних рівнів тимчасових рядів використовуються методи, розраховані для статистичних сукупностей.

Метод Ірвіна – припускає використання наступної формули:

,

де – середньоквадратичне відхилення, що розраховується у свою чергу з використанням формул:

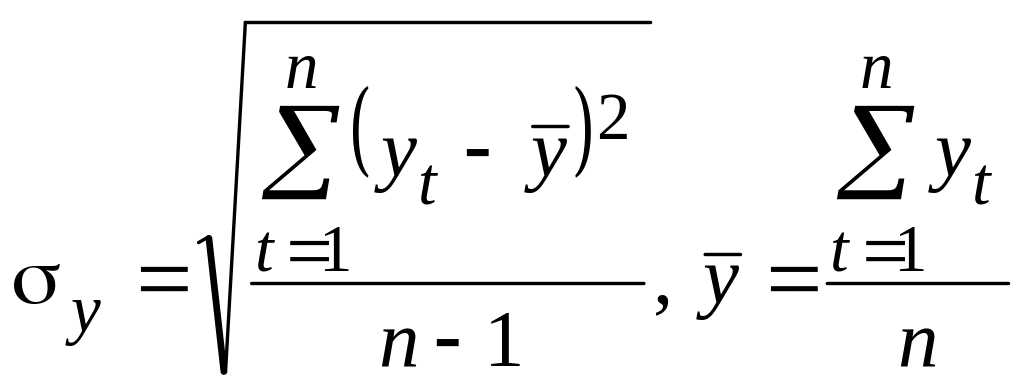
Розрахункові значення , і т. д. порівнюються з табличними значеннями критерію Ірвіна і якщо виявляються більше за табличні, то відповідне значення рівня ряду вважається аномальним. Значення критерію Ірвіна для рівня значимості , тобто з 5%-вою помилкою, приведені в табл. 12.4.

Таблиця 12.4. Критичні значення критерію Ірвіна для рівня значимості

	2	3	10	20	30	50	100
	2,8	2,3	1,5	1,3	1,2	1,1	1,0

Для визначення наявності тренду в початковому часовому ряду застосовується декілька методів.

1. Метод перевірки різниць середніх рівнів. Реалізація цього методу складається з чотирьох етапів.

На першому етапі початковий часовий ряд розбивається на дві приблизно рівні по числу рівнів частини: в першій частині перших рівнів початкового ряду, в другій – інших рівнів . Умови застосування методу - монотонність ряду. Розбиття ряду виконується, як правило навпіл, якщо ряд не монотонний, розбиття виконують в певних пропорціях, наприклад 1/3, 2/3.

На другому етапі для кожної з цих частин обчислюються середні значення і дисперсії:

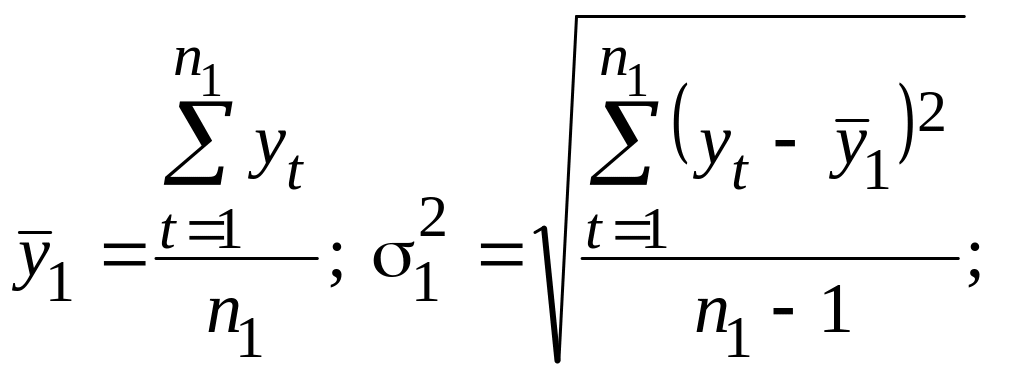
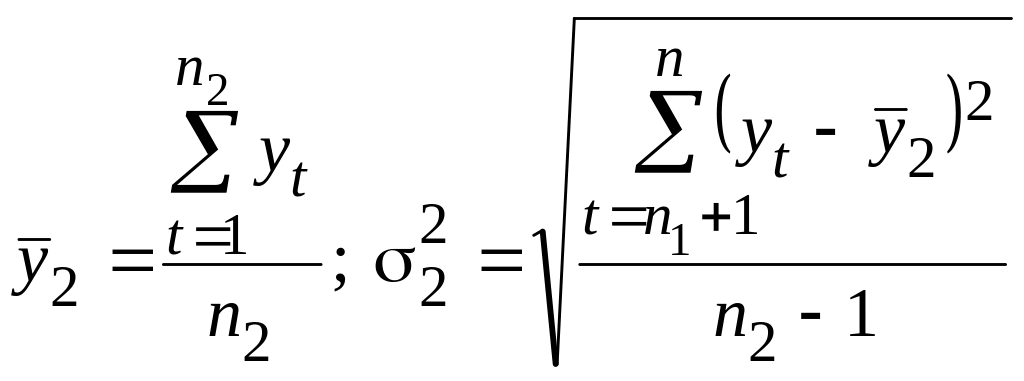
Третій етап полягає в перевірці рівності (однорідності) дисперсій обох частин ряду за допомогою -критерію Фішера, яка заснована на порівнянні розрахункового значення цього критерію:

з табличним (критичним) значенням із заданим рівнем значимості (рівнем помилки) . В якості найчастіше беруть значення 0,1 (10%-на помилка), 0,05 (5%-на помилка), 0,01 (1%-на помилка). Величина називається довірчою вірогідністю. Кількість ступенів свободи визначається як .

При цьому: ;

Якщо розрахункове значення менше за табличне , то гіпотеза про рівність дисперсій приймається і переходять до четвертого етапу. Якщо більше або рівно табличного , то гіпотеза про рівність дисперсій відхиляється і робиться висновок, що цей метод для визначення наявності тренду відповіді не дає.

На четвертому етапі перевіряється гіпотеза про відсутність тренду з використанням -критерію Стьюдента. Для цього визначається розрахункове значення критерію Стьюдента за формулою:

,

де – середньоквадратичне відхилення різниці середніх:

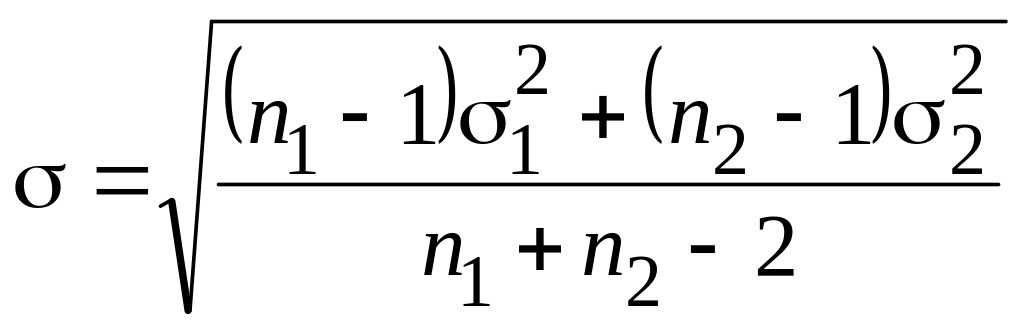
При цьому: ;

Якщо розрахункове значення менше табличного значення статистики Стьюдента із заданим рівнем значимості , гіпотеза приймається, тобто тренду немає, інакше тренд є. Помітимо, що в даному випадку табличне значення береться для числа ступенів свободи, рівного , при цьому цей метод застосовний тільки для рядів з монотонною тенденцією.

2. Метод Фостера-Стьюарта. Цей метод має більше можливостей і дає надійніші результати в порівнянні з попереднім. Окрім тренду самого ряду (як то кажуть, тренду в середньому), він дозволяє встановити наявність тренду дисперсії часового ряду: якщо тренду дисперсії немає, то розкид рівнів ряду постійний; якщо дисперсія збільшується, то ряд «розгойдується» і т. д.

Реалізація методу також містить чотири етапи.

На першому етапі порівнюють кожний рівень початкового часового ряду, починаючи з другого рівня, з усіма попередніми, при цьому визначають дві числові послідовності:

На другому етапі обчислюють величини і :

;

Величина , що характеризує зміну часового ряду, набуває значень від 0 (усі рівні ряду рівні між собою) до (ряд монотонний). Величина характеризує зміну дисперсії рівнів часового ряду і змінюється від (ряд монотонно спадає) до (ряд монотонно зростає).

Третій етап полягає в перевірці гіпотез:

– чи можна вважати випадковим відхилення величини від величини – математичного очікування величини для ряду, в якому рівні розташовані випадковим чином,

– відхилення величини від нуля.

Ця перевірка проводиться з використанням розрахункових значень -критерія Стьюдента для середньої і для дисперсії:

;

,

де – математичне очікування величини , визначеною для ряду, в якому рівні розташовані випадковим чином; - середньоквадратичне відхилення для величини ; - середньоквадратичне відхилення для величини d.

Для зручності є табульовані значення величин , і ; фрагменти цих значень представлені в табл.

Таблиця Значення , і

	10	20	30	40
	3,858	5,195	5,990	6,557
	1,288	1,677	1,882	2,019
	1,964	2,279	2,447	2,561

На четвертому етапі розрахункові значення і порівнюються з табличним значенням -критерія Стьюдента із заданим рівнем значимості . Якщо розрахункове значення менше за табличне, то гіпотеза про відсутність відповідного тренду приймається; інакше тренд є. Наприклад, якщо більше табличного значення , a менше , то для цього часового ряду є тренд в середньому, а тренду дисперсії рівнів ряду немає.