2. Точка спроса и её характеристика.

Если функция полезности строго вогнута, то решение задачи потребителя единственно, т.е. су­ществует только одна точка максимума функции полезности на бюджетном множестве.

Доказательство:

Предположим, что А и С две такие точки максимума. Так как речь идёт о глобальном макси­муме, т.е. максимуме на всём бюджетном множестве, то сам максимум . Рассмотрим точку . Видно, что , т.е. . Учитывая строгую вогнутость функции, имеем . Поскольку любая точка максимума лежит на границе бюджетного множества, то обе точки лежат на его границе, т.е. . Таким образом, до­пустив существование 2-х точек максимума, получим противоречие.

При строгой вогнутости функции потребления в бюджетном множестве существует единствен­ная точка ее максимума. Таким образом, у потребителя даже нет выбора того, как с наибольшей пользой потратить свои деньги, так как существует единство наборов товаров максимизирующих полезность. Эта единственная точка максимума называется точкой спроса или просто спросом по­требителя. Будем обозначать её . Изучим эту точку.

Пока о ней известно что:

• она существует;

• она единственная;

• она лежит на границе в бюджетном множестве.

Таким образом, задача потребителя сводится к следующей:

Эту задачу можно решить с помощью множителей Лагранжа. Составим функцию Лагранжа: . Найдём частные производные и прировняем их к нулю:

Вывод: точка спроса лежит на границе бюджетного множества и характеризуется тем, что в ней вектор предельной полезности пропорционален вектору цен .

Можно сказать и так: в точке спроса относительная предельная полезность товара к его цене есть величина постоянная для любого .

Также в точке спроса предельная норма замещения j-ro товара i-м равна обратному отношению цен , т.е. индивиду не выгодно потреблять одно благо вместо другого, стоящего столько же и вообще как-то изменять структуру потребления, поскольку всякое такое изменение только ухудшит его благосостояние – II закон Гёссе.

Первое соотношение показывает, что предел полезности товара в точке спроса, приходящейся на одну единицу его цены, т.е. на одну денежную единицу, один и тот же для всех товаров. Дру­гими словами оптимальный множитель Лагранжа равный отношению предельной полезности к цене измеряется в полезных единицах любого товара, что сводится к полезности на гривну. Сле­довательно, необходимо интерпретировать как предельную полезность добавленного до­хода , который называется пределом полезности денег.

Этот результат мог быть получен так же из следующего рассуждения. Пусть доход Q является изменяемой величиной, тогда и станут зависеть от и максимальное значение функции Лагранжа так же, в конечном счете, станет зависеть от :

.

Найдём производную по :

Так как , то , как и выражение , получим .

Пример 1.

Найти точку спроса потребителя с бюджетным множеством .

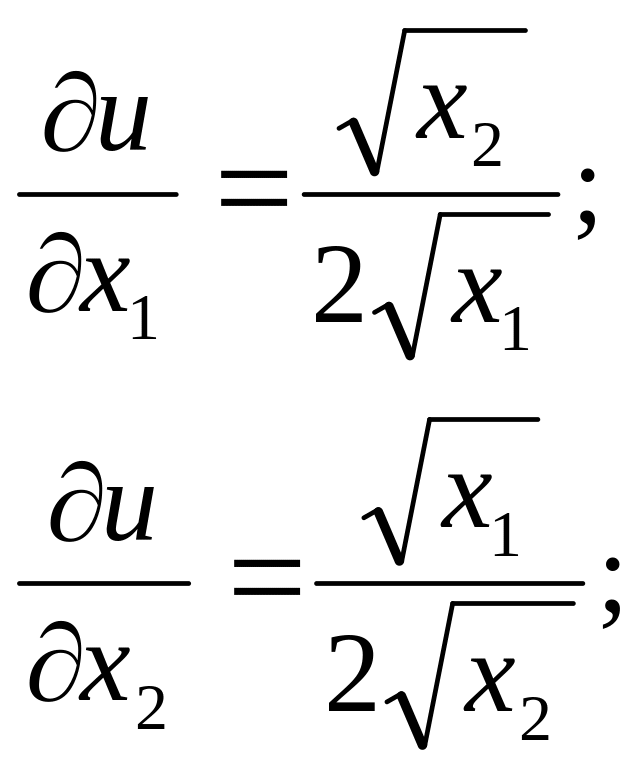
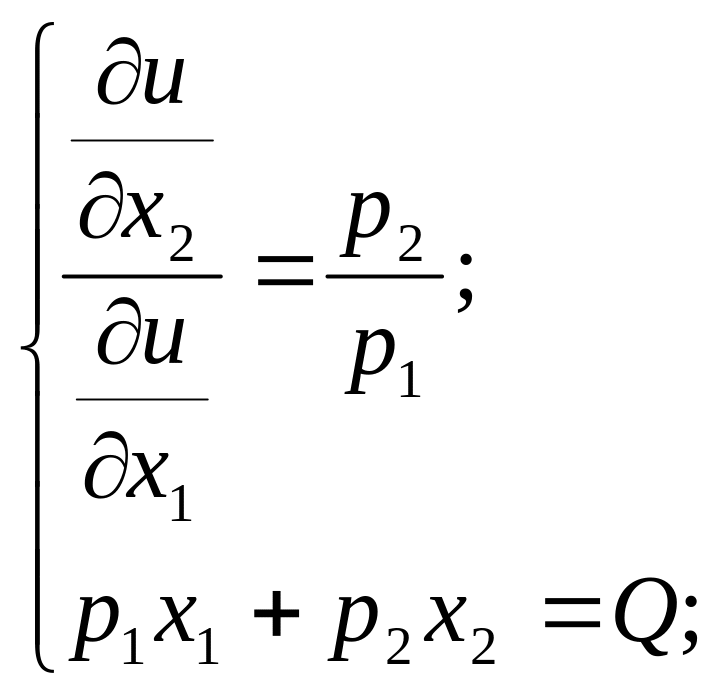
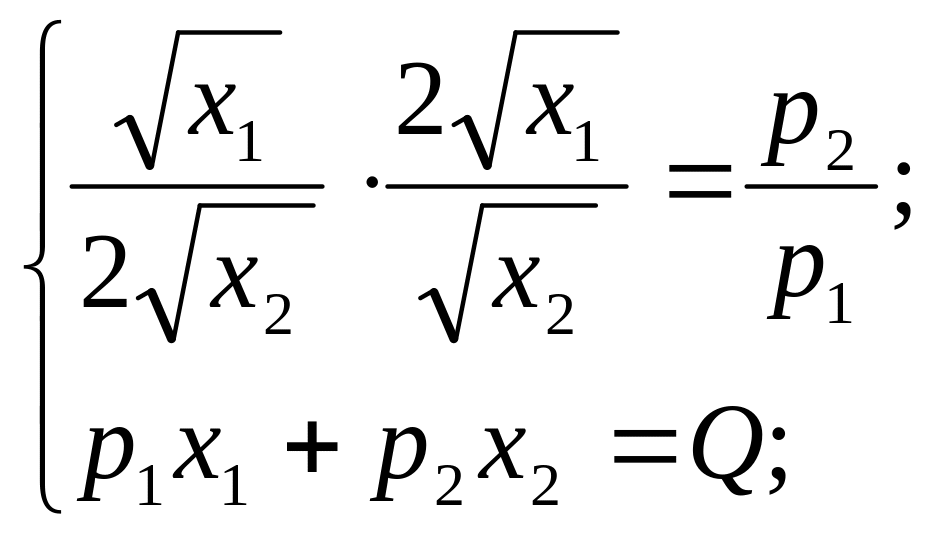
3. Функция спроса.

Итак, если бюджетное множество строго вогнуто и удовлетворяет некоторым условиям диффе­ренцируемости, и все цены строго положительны, то при любом данном доходе задача опре­деления набора товаров, которое можно купить при этом доходе и имеющем наибольшую полез­ность имеет единственное решение.

Это решение называется точкой спроса. Как легко увидеть, точка спроса зависит от до­хода и цены . То есть, точка спроса есть функция цен и дохода. Эта функция и называется функцией спроса.

Функция спроса – это вектор-функция своих аргументов: цен и дохода .

Рассматривая компоненты вектора , т.е. количество товаров можно сказать, что функция спроса – это набор n-функций.

Вышеперечисленные функции – это обычные функции от переменных, цен и до­хода . Они называются функциями спроса соответственных товаров.

При некоторых исходных предложениях функции спроса непрерывно зависят от своих аргу­ментов и даже дифференцируются по них.

Считаем, что функции спроса имеют все производные. Под производной функции спроса по­нимают вектор, т.е. набор соответственных производных от функции спроса на отдельные товары.